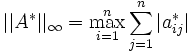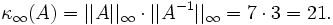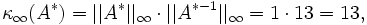Spaltenäquiliberung

Unter Äquilibrierung (lat.aequilibrium=Gleichgewicht) versteht man in der numerischen Mathematik die Multiplikation der Zeilen oder Spalten eines linearen Gleichungssystems mit bestimmten Faktoren, so dass anschließend alle Zeilen bzw. Spalten die gleiche Norm besitzen. Ziel dieser Skalierung ist es, die Konditionszahl des Gleichungssystems zu verringern, was den Einfluss von Störungen der Eingabedaten (z. B. durch Rundungsfehler) auf die Lösung verringert.

Äquilibrierung ist damit eine Möglichkeit der Vorkonditionierung linearer Gleichungssysteme, allerdings im Regelfall nicht besonders effektiv, da die durch die Diagonalmatrix gegebene Approximation der Inversen nicht gut ist. Etwa bei den meisten Diskretisierungsverfahren für partielle Differentialgleichungen, sind andere Vorkonditionierer vorzuziehen.

Mathematische Beschreibung

Ziel der Äquilibrierung ist das Ersetzen des Gleichungssystems Ax = b durch ein äquivalentes Gleichungssystem mit Systemmatrix A ^* mit möglichst kleiner Konditionszahl. Dabei hängt die Konditionszahl von der Matrixnorm ab und diese Verkleinerung gelingt nicht zwingend bezüglich jeder Matrixnorm. Man kann allerdings für die Zeilensummennorm und die Spaltensummennorm optimale Skalierungen angeben.

Zeilenäquilibrierung

Eine Zeilenäquilibrierung entspricht der Multiplikation der Matrix A von links mit einer Diagonalmatrix D. Durch Skalierung der Zeilen mit der Betragssummennorm wird die Kondition 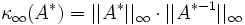$\kappa_{\infty}(A^*) = \vert\vert A^* \vert\vert_{\infty} \cdot \vert\vert A^{*-1} \vert\vert_{\infty}$ des skalierten Gleichungssystems bezüglich der Zeilensummennorm

$\vert\vert A^* \vert\vert_{\infty} = \max_{i=1}^n \sum_{j=1}^n {|a^*_{ij}|}$

optimiert. Es gibt also keine Diagonalmatrix 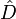$\hat{D}$, so dass 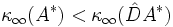$\kappa_{\infty}(A^*)<\kappa_{\infty}(\hat{D}A^*)$. Dabei wird jede Zeile i der Matrix A durch ihre Zeilensumme 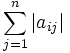$\sum_{j=1}^{n} \vert a_{ij} \vert$ geteilt (diese Summe ist größer als 0, da die Matrix als regulär vorausgesetzt wurde).

Spaltenäquilibrierung

Eine Äquilibrierung der Spalten entspricht der Multiplikation der Matrix A von rechts mit einer Diagonalmatrix. Skalierung der Spalten über die Betragssummennorm, indem man durch die Spaltensummen 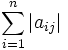$\sum_{i=1}^{n} \vert a_{ij} \vert$ teilt, liefert eine optimale Skalierung bezüglich der Spaltensummennorm in dem Sinne, dass keine Diagonalmatrix 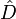$\hat{D}$ existiert, so dass $\kappa_{1}(A^*)<\kappa_{1}(A^*\hat{D})$.

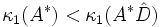Beispiel

Anhand eines kurzen Beispiels soll die Zeilenäquilibrierung demonstriert werden. Gegeben sei die Matrix A zum linearen Gleichungssystem Ax = b.

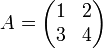$A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ mit der Inversen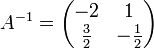 $A^{-1} = \begin{pmatrix} -2 & 1 \\ \frac{3}{2} & -\frac{1}{2} \end{pmatrix}$

Damit ist die Kondition der Matrix bezüglich der Zeilensummennorm

$\kappa_{\infty}(A) = \vert\vert A \vert\vert_{\infty} \cdot \vert\vert A^{-1} \vert\vert_{\infty} = 7 \cdot 3 = 21.$

Bei der Zeilenäquilibrierung wird nun die folgende Diagonalmatrix 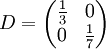$D = \begin{pmatrix} \frac{1}{3} & 0 \\ 0 & \frac{1}{7} \end{pmatrix}$ (aufgestellt wie oben beschrieben) von links heranmultipliziert. Damit ergibt sich

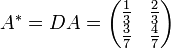$A^* = DA = \begin{pmatrix} \frac{1}{3} & \frac{2}{3} \\ \frac{3}{7} & \frac{4}{7} \end{pmatrix}$ mit der Inversen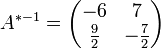 $A^{*-1} = \begin{pmatrix} -6 & 7 \\ \frac{9}{2} & -\frac{7}{2} \\ \end{pmatrix}$

Die Kondition der Matrix A ^* berechnet sich zu

$\kappa_{\infty}(A^*) = \vert\vert A^* \vert\vert_{\infty} \cdot \vert\vert A^{*-1} \vert\vert_{\infty} = 1 \cdot 13 = 13,$

was kleiner ist als die Kondition der Matrix A. Der Wert 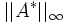$\vert\vert A^* \vert\vert_{\infty}$ ist hierbei aufgrund der Definition von A ^* immer 1.

Literatur

• A. Meister: Numerik linearer Gleichungssysteme. 2. Auflage. Vieweg, 2005, ISBN 3528131357
• A. Kielbasinski und H. Schwetlick: Numerische lineare Algebra. Deutscher Verlag der Wissenschaften, 1988