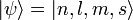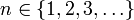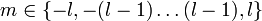Spinquantenzahl

Quantenzahlen dienen in der Quantenmechanik der Beschreibung von Eigenschaften bestimmter Teilchen. Ein Satz von Quantenzahlen charakterisiert einen Eigenzustand eines quantenmechanischen Systems vollständig. Sie können im Gegensatz zu Beschreibungsgrößen der klassischen Mechanik nur diskrete Werte annehmen. Es gibt verschiedene Quantenzahlen für jeweils verschiedene Eigenschaften oder auch für die unterschiedlichen Teilchen.

Quantenzahlen sind aufgrund ihrer Diskretheit im Vergleich zur klassisch-kontinuierlichen Welt unintuitiv. Es ist aber gerade Wesen der Quantenmechanik, dass bestimmte Werte nur exakt und gestuft/diskret vorkommen.

Eine sehr große Bedeutung kommt den Quantenzahlen neben der Atomphysik auch in der subatomaren Physik der Teilchenphysik zu. Dort dienen sie zur Kennzeichnung der Kerne und Teilchen sowie zur Beschreibung der Übergänge zwischen ihnen.

Gebundenes Elektron im Wasserstoff-Atom

Die Eigenzustände des gebundenen Elektrons und seine Wellenfunktion im Wasserstoffatom werden durch vier Quantenzahlen beschrieben:

$| \psi\rangle =| n, l, m, s \rangle$

Hauptquantenzahl

Die Hauptquantenzahl n beschreibt im Schalenmodell die Schale, in der sich das Elektron mit einer Wahrscheinlichkeit von 90% aufhält. Sie bezeichnet das grundlegende Energieniveau, und kann beliebige natürliche Zahlen größer Null annehmen:

$n \in \{1,2,3,\ldots\}$

Dies entspricht immer höheren Anregungen, bei sehr großem n spricht man von Rydberg-Atomen. Das Energieniveau ergibt sich aus der Hauptquantenzahl mit:

$E_n =-{ m e^4 \over 8 \epsilon_0^2 h^2 } \cdot {1 \over n^2} = -R_H { 1 \over n^2}$.

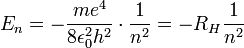(mit R_H = 13,6 eV (Rydberg-Konstante))

für das Wasserstoffatom.

Nebenquantenzahl

Die Nebenquantenzahl l oder auch Drehimpulsquantenzahl l kennzeichnet die Form des Orbitals in einem Atom. Sie kann 0 sowie beliebige natürliche Zahlen annehmen, muss aber auf jeden Fall kleiner als n sein:

$l \in \{0,1,2,\ldots,n-1\}$

Nebenquantenzahlen werden auch häufig mit den entsprechenden Buchstaben gekennzeichnet:

$l \in \{0,1,2,\ldots,n-1\}$

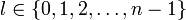
Symbol: s,p,d,f

Der Name "Drehimpulsquantenzahl" ist historisch und geht auf die Vorstellung zurück, dass diese Quantenzahl den Drehimpuls des sich um den Atomkern bewegenden Elektrons beschreibt. Siehe Bohr-Sommerfeldsches Atommodell. Gleichzeitig ist 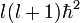$l(l+1)\hbar^2$ der Eigenwert des Drehimpulsoperators L².

Magnetische Quantenzahl des Drehimpuls

Die magnetische Quantenzahl des Drehimpuls, wird mit m bezeichnet, und beschreibt die räumliche Orientierung des Elektronen-Bahndrehimpuls. Sie darf betragsmäßig nicht größer sein als die Nebenquantenzahl l, darf dafür aber auch negative Werte annehmen:

$m \in \{-l, -(l-1) \ldots (l-1), l\}$

Sie heißt Magnetquantenzahl, weil die zusätzliche potentielle Energie in einem Magnetfeld in z-Richtung (normaler Zeeman-Effekt) von ihr abhängt (bei m = 0 keine z-Komponente, d.h. keine zusätzliche Energie; bei m = l nur z-Komponente, d.h. maximale zusätzliche Energie).

Spinquantenzahl

Hauptartikel: Spin

Die Spinquantenzahl s des Elektrons beschreibt die Orientierung des Spins des Elektrons. Sie ist halbzahlig: 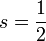$s = \frac{1}{2}$ Für die Projektion des Spins in z-Richtung gibt es nur zwei Möglichkeiten: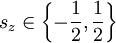 $s_z \in \left\{-\frac{1}{2},\frac{1}{2}\right\}$

Weitere Quantenzahlen

Gesamtdrehimpulsquantenzahl

Die Gesamtdrehimpulsquantenzahl beschreibt den Gesamtdrehimpuls eines Elektrons, bei dem (anschaulich) der Spin mit dem Drehimpuls koppelt, und eine Unterscheidung der Drehimpulse nicht mehr möglich ist.

Für die Quantenzahl gilt z.B. bei LS-Kopplung: J = (L + S),(L + S − 1),..., | L − S |

Kernspinquantenzahl

Hauptartikel: Kernspin

Die Kernspinquantenzahl (auch Kernspin oder Richtungsquantenzahl genannt) beschreibt den Drehimpuls von Atomkernen. Sie setzt sich aus dem Spin der einzelnen Neutronen und Protonen zusammen, und kann daher positive ganz- oder halbzahlige Werte annehmen.

Mehr-Elektronen-Systeme

Im Unterschied zum Wasserstoffatom bestehen die Hüllen anderer Atome aus mehreren Elektronen, die sich gegenseitig beeinflussen. Dennoch kann man ihren Zustand oft näherungsweise durch obige Quantenzahlen beschreiben; um solche Systeme aber von Ein-Elektron-Systemen zu unterscheiden, werden dann die Quantenzahlen mit großen Buchstaben geschrieben. Z.B. beschreibt S dann den Gesamt-Spin aller Elektronen.

Es ist aber zu beachten, dass Elektronen dem Pauli-Prinzip unterliegen, da sie Fermionen sind: Keine zwei Elektronen dürfen in allen Quantenzahlen übereinstimmen.

Siehe auch

• Elektronenkonfiguration
• Orbitale

Literatur

• Haken, Wolf: Atom- und Quantenphysik. 8. Auflage. Springer-Verlag, Berlin Heidelberg New York 2004, ISBN 3-540-02621-5