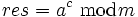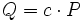Square and Multiply

Unter dem Schnellen Potenzieren versteht man ein mathematisch optimiertes Verfahren, dessen bekanntester Vertreter das „Square & Multiply“ ist. Es stellt eine Möglichkeit dar, um die Berechnung von natürlichen Zahlen mit großen Exponenten zu beschleunigen, in dem es versucht, Rechenoperationen einzusparen.

Square & Multiply

Das „Square-&-Multiply“-Verfahren beschreibt eine Methode, um schnell Potenzen zu berechnen.

Einsatzgebiete

Das Verfahren ist für folgende zwei Fragestellungen geeignet:

• a^c
• $a^c \,\mathrm{mod}\, n$

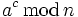
Das Verfahren ist nicht nur auf die Multiplikation beschränkt, sondern kann für verschiedenste Operationen (z. B. Elliptische Kurven-Addition) adaptiert werden.

Verfahren

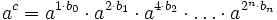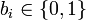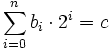„Square & Multiply“ nutzt die Tatsache, dass a^c eindeutig als $a^c = a^{1\cdot b_0} \cdot a^{2\cdot b_1} \cdot a^{4\cdot b_2} \cdot \dots \cdot a^{2^n \cdot b_n}$ geschrieben werden kann, wobei $b_i \in \{0,1\}$ und $\sum_{i=0}^{n} b_i \cdot 2^i = c$. Die b_is sind also die Stellen von c in der Darstellung als Binärzahl.

Dies kann man wiederum umformen und erhält folgende Form: $a^c= a^{b_0}(a^{b_1}(\dots(a^{b_{n-1}}(a^{b_n})^2)^2\dots)^2)^2$

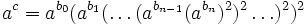
Algorithmus

Gegeben:

• a ... Basis (Zahl, die potenziert werden soll)
• c ... Exponent
• b ... Binärdarstellung von c, wobei das höchstwertige Bit an der Stelle n steht und das niedrigstwertige Bit an der Stelle 0; (b hat n+1 Ziffern)
• m ... Modulus

Gesucht:

• $res=a^c\;\bmod{m}$

Ablauf:

Square & Multiply
res = a for i=n-1..0 res = res^2 mod m if b_i = 1 res = (res * a) mod m end-if end-for

Wenn keine modulare Reduzierung vonnöten ist, wird diese einfach weggelassen.

Möchte man die Punktmultiplikation für elliptische Kurven implementieren, muss man die Quadrierung und die Multiplikation durch das jeweilige Äquivalent ersetzen. Der adaptierte Algorithmus hätte folgende Form.

Gegeben:

• P ... Punkt, der multipliziert werden soll (Punktmultiplikation)
• c ... Multiplikator
• b ... Binärdarstellung von c, wobei das höchstwertigste Bit an der Stelle n steht und das niederwertigste Bit an der Stelle 0
• INF ... Unendlichkeits- oder Nullpunkt (neutrales Element)

Gesucht:

• $Q=c \cdot P$

Square & Multiply für elliptische Kurven
Q=INF for i=n..0 Q = 2*Q if b_i = 1 Q = Q + P end-if end-for

Beispiel

Gegeben:

• a = 2
• c = 11
• b = 1011

res = 1

• Schleifendurchlauf 1: b₃ = 1

res = res² = 1

res = res * a = 2

• Schleifendurchlauf 2: b₂ = 0

res = res² = 4

• Schleifendurchlauf 3: b₁ = 1

res = res² = 16

res = res * a = 32

• Schleifendurchlauf 4: b₀ = 1

res = res² = 1024

res = res * a = 2048

Laufzeitanalyse

Bei der einfachen und langsamen Potenzierung von a^c multipliziert man a (c − 1)-mal mit sich selbst. Beim „Square & Multiply“ werden lediglich log₂(c) Schleifendurchläufe benötigt (log₂(c) entspricht hierbei ungefähr der Länge der Zahl c in der Binärdarstellung). In jedem Schleifendurchlauf kommt es zu einer Quadrierung (wobei die erste Quadrierung vernachlässigt werden kann) und eventuell einer Multiplikation. Asymptotisch werden O(log(c)) Operationen (die Basis des Logarithmus ist in diesem Fall nicht von Bedeutung) benötigt, wogegen O(c) Operationen bei der einfachen Potenzierung zu Buche schlagen. O bezeichnet eine asymptotische obere Schranke für das Laufzeitverhalten des Algorithmus. Wie man leicht einsieht, ist das „Square-&-Multiply“-Verfahren sehr viel effizienter als das einfache Verfahren. Dieser verringerte Anspruch an die Rechenleistung ist bei großen Basen und Exponenten enorm.

Weblinks

• Applet zur Visualisierung des Verfahrens