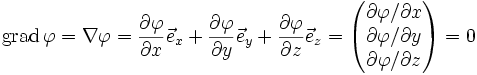Kritischer Punkt (Mathematik) — Eine stetig differenzierbare Abbildung zwischen zwei differenzierbaren Mannigfaltigkeiten besitzt an einer Stelle einen kritischen oder stationären Punkt, falls dort das Differenzial nicht surjektiv ist. Andernfalls handelt es sich um einen… … Deutsch Wikipedia
Flächen [1] — Flächen, zweidimensionale Gebilde, entweder eben oder krumm (vgl. Flächentheorie). Geometrische Eigenschaften der Flächen. Flächen, krumme. Eine krumme Fläche ist der geometrische Ort aller Lagen einer nach einem bestimmten Gesetze bewegten Kurve … Lexikon der gesamten Technik
Enneperfläche — Eine Minimalfläche ist eine Fläche im Raum, die lokal minimalen Flächeninhalt hat. Derartige Formen nehmen beispielsweise Seifenhäute an, sofern sie nicht wie im Fall von Blasen durch eingeschlossene Luft aufgebläht werden. In mathematischer… … Deutsch Wikipedia
Helicoid — Eine Minimalfläche ist eine Fläche im Raum, die lokal minimalen Flächeninhalt hat. Derartige Formen nehmen beispielsweise Seifenhäute an, sofern sie nicht wie im Fall von Blasen durch eingeschlossene Luft aufgebläht werden. In mathematischer… … Deutsch Wikipedia
Minimalfläche — Eine Minimalfläche ist eine Fläche im Raum, die lokal minimalen Flächeninhalt hat. Derartige Formen nehmen beispielsweise Seifenhäute an, wenn sie über einen entsprechenden Rahmen (wie etwa einem Blasring) gespannt sind. In mathematischer Sprache … Deutsch Wikipedia
Scherkfläche — Eine Minimalfläche ist eine Fläche im Raum, die lokal minimalen Flächeninhalt hat. Derartige Formen nehmen beispielsweise Seifenhäute an, sofern sie nicht wie im Fall von Blasen durch eingeschlossene Luft aufgebläht werden. In mathematischer… … Deutsch Wikipedia
Wendelfläche — Eine Minimalfläche ist eine Fläche im Raum, die lokal minimalen Flächeninhalt hat. Derartige Formen nehmen beispielsweise Seifenhäute an, sofern sie nicht wie im Fall von Blasen durch eingeschlossene Luft aufgebläht werden. In mathematischer… … Deutsch Wikipedia
Rayleigh-Koeffizient — Der Rayleigh Quotient des n Vektors x zur quadratischen Matrix A ist die Zahl mit . Der Rayleigh Quotient hat eine enge Beziehung zu den Eigenwerten von A. Ist x ein Eigenvektor der Matrix A und λ der zugehörige Eigenwert, dann gilt … Deutsch Wikipedia
Pflegeversicherung (Deutschland) — Die Soziale Pflegeversicherung (PV) in Deutschland ist der jüngste eigenständige Zweig der Sozialversicherung. Er wurde mit Wirkung zum 1. Januar 1995 durch Verabschiedung des Elften Buches Sozialgesetzbuch (SGB XI)[1] als… … Deutsch Wikipedia
Berührung — Berührung. Man sagt von zwei (ebenen oder räumlichen) Kurven oder einer Kurve und einer Fläche oder zwei Flächen, sie berühren einander in einem Punkt, in den ersten beiden Fällen, wenn in diesem Punkt eine gemeinschaftliche Tangente, im letzten… … Lexikon der gesamten Technik
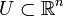 eine offene Menge und
eine offene Menge und 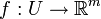 eine Funktion. Ein Punkt
eine Funktion. Ein Punkt 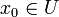 heißt kritischer oder stationärer Punkt von f, genau dann wenn
heißt kritischer oder stationärer Punkt von f, genau dann wenn 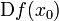 nicht surjektiv ist, d.h. wenn
nicht surjektiv ist, d.h. wenn 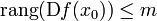 gilt, wobei
gilt, wobei 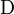 das totale Differential bezeichnet.
das totale Differential bezeichnet.