- Stieltjes'scher Inhalt
-
Der Stieltjes’sche Inhalt, benannt nach dem Mathematiker T. J. Stieltjes, ist ein Inhalt, mit dem man das Riemann-Integral zum Stieltjes’schen Integral verallgemeinern kann.
Der Stieltjes’sche Inhalt wird auf dem Halbring
![\mathcal{J}:=\{]a,b]:a,b\in \mathbb{R}, a\le b\}](/pictures/dewiki/98/b6e35fd7d13fb6f22a82e13d2ca4510f.png) über R definiert. Da man Inhalte auf einem Halbring eindeutig auf ihrem erzeugten Ring fortsetzen kann (Vgl. Elsrodt II.1.6), ist damit auch das zugehörige Prämaß auf
über R definiert. Da man Inhalte auf einem Halbring eindeutig auf ihrem erzeugten Ring fortsetzen kann (Vgl. Elsrodt II.1.6), ist damit auch das zugehörige Prämaß auf 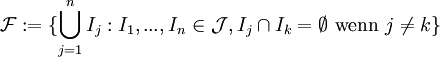 bekannt.
bekannt.Inhaltsverzeichnis
Definition
Gegeben eine wachsende Funktion
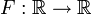 , so nennt man
, so nennt man ![\mu_F : \mathcal {J} \rightarrow \mathbb {R}, \mu_F(]a,b]):=F(b)-F(a), (a\le b)](/pictures/dewiki/97/ae80a14a7698eabaea0df89bef203975.png) den zu F gehörenden Stieltjes'schen Inhalt.
den zu F gehörenden Stieltjes'schen Inhalt.Aussehen des Inhalts
Ist
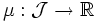 ein endlicher Inhalt und wird
ein endlicher Inhalt und wird 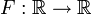 definiert durch
definiert durch ![F(x):=\begin{cases} \mu (]0,x]), & \mbox{wenn }x \ge 0 \\ - \mu (]x,0]), & \mbox{wenn }x<0 \end{cases}](/pictures/dewiki/102/fd10370ef307e15559f5794410dcc400.png) , so gilt μ = μF.
, so gilt μ = μF.Damit hat also der Stieltjes’sche Inhalt obige Form.
Prämaß
Man ist oft daran interessiert, statt einem Inhalt ein Prämaß zu erhalten, da es eine größere Urbildmenge hat. Ist der Stietlje’sche Inhalt also ein Prämaß? Das ist genau dann der Fall, wenn F rechtsstetig ist.
Stieltjes’sches Integral
Mithilfe des Stieltjes’schen Inhalts kann man das Riemann-Integral zum Stieltjes’schen Integral
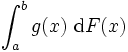 erweitern. (Vgl. Walter)
erweitern. (Vgl. Walter)Für F=id ist das Stieltjes’sche Integral gerade gleich dem Riemann’schen.
Literatur
- W. Walter: Grundwissen-Band Analysis II.
- Jürgen Elstrodt: Maß- und Integrationstheorie. 4. korrigierte Auflage. Springer, Berlin/Heidelberg/New York 2005, ISBN 3-540-21390-2, Kapitel II § 2, S. 37.
Wikimedia Foundation.
