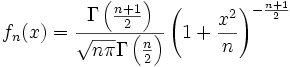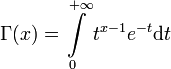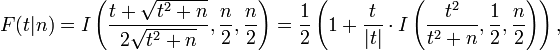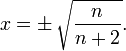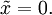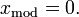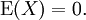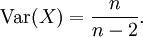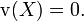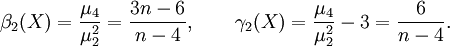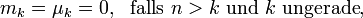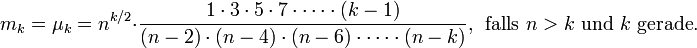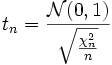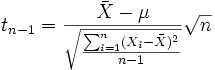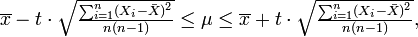Studentverteilung

Dichten von t-verteilten Zufallsgrößen

Die Studentsche t-Verteilung (auch Student-t-Verteilung) ist eine Wahrscheinlichkeitsverteilung, die 1908 von William Sealey Gosset entwickelt wurde.

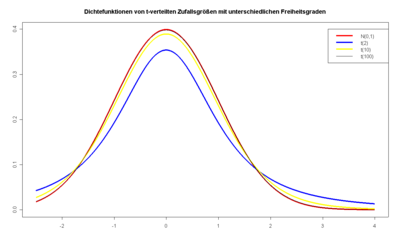
Er hatte festgestellt, dass der standardisierte Mittelwert normalverteilter Daten nicht mehr normalverteilt, sondern t-verteilt ist, wenn die Varianz des Merkmals unbekannt ist und mit der Stichprobenvarianz geschätzt werden muss. Die t-Verteilung zeigt für kleine Werte des Parameters n eine größere Breite und Flankenbetonung als die Normalverteilung (siehe Grafik rechts). Hypothesentests, bei denen die t-Verteilung Verwendung findet, bezeichnet man als t-Tests.

Die Herleitung wurde erstmals 1908 veröffentlicht, während Gosset in einer Guinness-Brauerei arbeitete. Da sein Arbeitgeber die Veröffentlichung nicht gestattete, veröffentlichte Gosset sie unter dem Pseudonym Student. Der t-Faktor und die zugehörige Theorie wurden erst durch die Arbeiten von R. A. Fisher belegt, der die Verteilung Student’s distribution (Students Verteilung) nannte.

Definition

Eine stetige Zufallsvariable X genügt der Studentschen t-Verteilung mit n Freiheitsgraden, wenn sie die Wahrscheinlichkeitsdichte

$f_n(x) = \frac{\Gamma\left(\frac{n+1}{2}\right)} {\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}}$

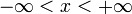für $-\infty < x < +\infty$ besitzt. Dabei ist

$\Gamma(x)=\int\limits_{0}^{+\infty}t^{x-1}e^{-t}\operatorname{d}t$

die Gamma-Funktion.

Verteilung

Die Verteilung lässt sich geschlossen ausdrücken als

$F(t|n)= I \left( \frac{t+\sqrt{t^2+n}}{2\sqrt{t^2+n}},\frac{n}{2},\frac{n}{2} \right)=\frac{1}{2}\left(1+\frac{t}{|t|} \cdot I \left( \frac{t^2}{t^2+n},\frac{1}{2},\frac{n}{2}\right)\right),$

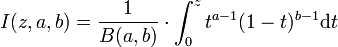wobei $I(z,a,b)=\frac{1}{B(a,b)}\cdot \int_0^z t^{a-1} (1-t)^{b-1}\mathrm{d}t$ die regularisierte unvollständige Betafunktion darstellt, und beide Ausdrücke verwendet werden können.

Eigenschaften

Wendepunkte

Die Dichte der t-Verteilung mit n Freiheitsgraden besitzt Wendepunkte bei

$x=\pm\,\sqrt{\frac{n}{n+2}}.$

Median

Der Median liegt bei

$\tilde{x}=0.$

Modus

Der Modus ergibt sich zu

$\,x_{\mathrm{mod}}=0.$

Erwartungswert

Für den Erwartungswert erhält man für n > 1

$\operatorname{E}(X)=0.$

Der Erwartungswert für n = 1 existiert nicht.

Varianz

Die Varianz ergibt sich für n > 2 zu

$\operatorname{Var}(X)=\frac{n}{n-2}.$

Schiefe

Die Schiefe ist für n > 3

$\operatorname{v}(X)=0.$

Wölbungen

Für die Kurtosis-Wölbung β₂ und die Exzess-Wölbung γ₂ erhält man für n > 4

$\operatorname{\beta_2}(X)=\frac{\mu_4}{\mu_2^2}=\frac{3n-6}{n-4},\qquad \operatorname{\gamma_2}(X)=\frac{\mu_4}{\mu_2^2}-3=\frac{6}{n-4}.$

Momente

Für die k-ten Momente 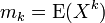$m_k=\operatorname{E}(X^k)$ und die k-ten zentralen Momente $\mu_k=\operatorname{E}([X-\operatorname{E}(X)]^k)$ gilt:

$m_k=\mu_k=0,~~\mathrm{falls~}n>k\mathrm{~und~}k\mathrm{~ungerade},$

$m_k=\mu_k=n^{k/2}\cdot\frac{1\cdot 3\cdot 5\cdot 7\cdot\dots\cdot(k-1)}{(n-2)\cdot(n-4)\cdot(n-6)\cdot\dots\cdot(n-k)}, ~~\mathrm{falls~}n>k\mathrm{~und~}k\mathrm{~gerade}.$

Nichtzentrale t-Verteilung

Ist der Zähler der t-verteilten Zufallsvariablen normalverteilt mit einem Erwartungswert 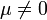$\mu\neq 0$, handelt es sich um eine so genannte nichtzentrale t-Verteilung mit dem Nichtzentralitätsparameter μ. Diese Verteilung wird vor allem zur Bestimmung des β-Fehlers bei Hypothesentests mit t-verteilter Prüfgröße verwendet.

Beziehung zu anderen Verteilungen

Beziehung zur Cauchy-Verteilung

Für n = 1 und mit 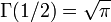$\Gamma(1/2)=\sqrt{\pi}$ ergibt sich die Cauchy-Verteilung als Spezialfall aus der Studentschen t-Verteilung.

Beziehung zur χ²-Verteilung und Standardnormalverteilung

Die t-Verteilung beschreibt die Verteilung eines Ausdruckes

$t_n=\frac{\mathcal{N}(0,1)}{\sqrt{\frac{\chi_n^2}{n}}}$

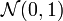wobei $\mathcal{N}(0,1)$ eine standardnormalverteilte und 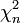$\chi_n^2$ eine χ²-verteilte Zufallsvariable mit n Freiheitsgraden bedeutet. Die Zählervariable muss unabhängig von der Nennervariable sein. Die Dichtefunktion der t-Verteilung ist dann symmetrisch bezüglich ihres Erwartungswertes 0. Die Werte der Verteilungsfunktion können nicht analytisch berechnet werden und liegen in der Regel tabelliert vor.

Näherung durch die Normalverteilung

Mit steigender Zahl von Freiheitsgraden kann man die Verteilungswerte der t-Verteilung mit Hilfe der Normalverteilung annähern. Als Faustregel gilt, dass ab 30 Freiheitsgraden die t-Verteilungsfunktion durch die Normalverteilung approximiert werden kann.

Verwendung in der mathematischen Statistik

Verschiedene Schätzfunktionen sind t-verteilt.

Beispielsweise gilt für die Schätzung des Erwartungswertes einer normalverteilten Grundgesamtheit: Wenn die unabhängigen Zufallsvariablen 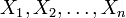$X_1, X_2, \dots , X_n$ identisch normalverteilt sind mit den Parametern μ und σ, dann unterliegt die stetige Zufallsgröße

$t_{n-1}=\frac{\bar{X}-\mu}{\sqrt{\frac{\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}}{n-1}}}\sqrt{n}$

einer Studentschen t-Verteilung mit (n − 1) Freiheitsgraden.

Das 95%-Konfidenzintervall für den Mittelwert μ wäre dann

$\overline{x}-t \cdot \sqrt{\tfrac{\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}}{n(n-1)}} \leq \mu \leq \overline{x}+t \cdot \sqrt{\tfrac{\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}}{n(n-1)}},$

wobei t durch F(t | n − 1) = 0.975 bestimmt ist. Dieses Intervall ist etwas größer als dasjenige, welches sich mit bekanntem σ aus der Verteilungsfunktion der Normalverteilung bei gleichem Konfidenzniveau ergeben hätte $\left( \mu =\overline{x}\pm 1.96 \cdot \tfrac{\sigma}{\sqrt{n}}\right)$.

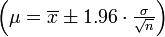Siehe auch

• Konfidenzintervall
• t-Test

Ausgewählte Quantile der t-Verteilung

v	Wahrscheinlichkeit
	0,75	0,875	0,90	0,95	0,975	0,99	0,995	0,999
1	1,000	2,414	3,078	6,314	12,706	31,821	63,657	318,309
2	0,816	1,604	1,886	2,920	4,303	6,965	9,925	22,327
3	0,765	1,423	1,638	2,353	3,182	4,541	5,841	10,215
4	0,741	1,344	1,533	2,132	2,776	3,747	4,604	7,173
5	0,727	1,301	1,476	2,015	2,571	3,365	4,032	5,893
6	0,718	1,273	1,440	1,943	2,447	3,143	3,707	5,208
7	0,711	1,254	1,415	1,895	2,365	2,998	3,499	4,785
8	0,706	1,240	1,397	1,860	2,306	2,896	3,355	4,501
9	0,703	1,230	1,383	1,833	2,262	2,821	3,250	4,297
10	0,700	1,221	1,372	1,812	2,228	2,764	3,169	4,144
11	0,697	1,214	1,363	1,796	2,201	2,718	3,106	4,025
12	0,695	1,209	1,356	1,782	2,179	2,681	3,055	3,930
13	0,694	1,204	1,350	1,771	2,160	2,650	3,012	3,852
14	0,692	1,200	1,345	1,761	2,145	2,624	2,977	3,787
15	0,691	1,197	1,341	1,753	2,131	2,602	2,947	3,733
16	0,690	1,194	1,337	1,746	2,120	2,583	2,921	3,686
17	0,689	1,191	1,333	1,740	2,110	2,567	2,898	3,646
18	0,688	1,189	1,330	1,734	2,101	2,552	2,878	3,610
19	0,688	1,187	1,328	1,729	2,093	2,539	2,861	3,579
20	0,687	1,185	1,325	1,725	2,086	2,528	2,845	3,552
21	0,686	1,183	1,323	1,721	2,080	2,518	2,831	3,527
22	0,686	1,182	1,321	1,717	2,074	2,508	2,819	3,505
23	0,685	1,180	1,319	1,714	2,069	2,500	2,807	3,485
24	0,685	1,179	1,318	1,711	2,064	2,492	2,797	3,467
25	0,684	1,178	1,316	1,708	2,060	2,485	2,787	3,450
26	0,684	1,177	1,315	1,706	2,056	2,479	2,779	3,435
27	0,684	1,176	1,314	1,703	2,052	2,473	2,771	3,421
28	0,683	1,175	1,313	1,701	2,048	2,467	2,763	3,408
29	0,683	1,174	1,311	1,699	2,045	2,462	2,756	3,396
30	0,683	1,173	1,310	1,697	2,042	2,457	2,750	3,385
40	0,681	1,167	1,303	1,684	2,021	2,423	2,704	3,307
50	0,679	1,164	1,299	1,676	2,009	2,403	2,678	3,261
60	0,679	1,162	1,296	1,671	2,000	2,390	2,660	3,232
70	0,678	1,160	1,294	1,667	1,994	2,381	2,648	3,211
80	0,678	1,159	1,292	1,664	1,990	2,374	2,639	3,195
90	0,677	1,158	1,291	1,662	1,987	2,368	2,632	3,183
100	0,677	1,157	1,290	1,660	1,984	2,364	2,626	3,174
200	0,676	1,154	1,286	1,653	1,972	2,345	2,601	3,131
300	0,675	1,153	1,284	1,650	1,968	2,339	2,592	3,118
400	0,675	1,152	1,284	1,649	1,966	2,336	2,588	3,111
500	0,675	1,152	1,283	1,648	1,965	2,334	2,586	3,107
$\infty$	0,674	1,150	1,282	1,645	1,960	2,326	2,576	3,090

Weblinks

• Webrechner für exakte Werte

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart