- Liste von Wahrscheinlichkeitsverteilungen
-
Es gibt unzählige Möglichkeiten, wie eine Zufallsvariable verteilt sein kann. Hier soll ein Überblick über die bekanntesten Wahrscheinlichkeitsverteilungen gegeben werden.
Inhaltsverzeichnis
Eigenschaften
Verteilungsfunktion
Die Verteilung ist durch die Verteilungsfunktion oder Dichtefunktion vollständig festgelegt. In der Tabelle wird die Verteilungsfunktion als F(x) = P({X < x}) definiert. Häufig wird die Verteilungsfunktion auch als
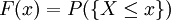 definiert. Für die "kleiner-gleich"-Definition ergeben sich Unterschiede insbesondere bei den diskreten Verteilungen; beispielsweise ist in den Summationsgrenzen die Aufrundungsfunktion
definiert. Für die "kleiner-gleich"-Definition ergeben sich Unterschiede insbesondere bei den diskreten Verteilungen; beispielsweise ist in den Summationsgrenzen die Aufrundungsfunktion 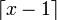 durch die Abrundungsfunktion
durch die Abrundungsfunktion 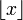 zu ersetzen.
zu ersetzen.Diskrete Verteilungen
-
Bezeichnung Kurzzeichen Vtlg. von X
Verteilungsfunktion F(x) = P({X < x})
Wahrscheinlichkeitsfunktion f(x) = P({X = x})
Binomialverteilung Bn,p 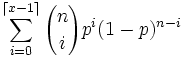
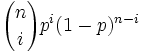
Negative Binomialverteilung NBn,p 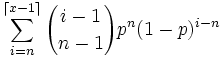
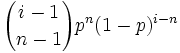
Geometrische Verteilung (Variante B) Gp 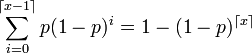
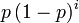
Hypergeometrische Verteilung HM,N,n 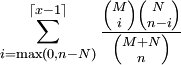
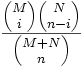
Poisson-Verteilung Pα 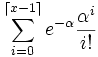
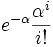
Diskrete Gleichverteilung DLn 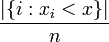
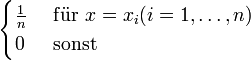
Stetige Verteilungen
-
Bezeichnung Kurzzeichen Vtlg. von X
Verteilungsfunktion F(x) = P({X < x})
Dichtefunktion Gleichverteilung La,b 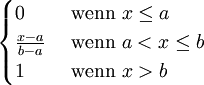
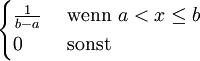
Exponentialverteilung Eα 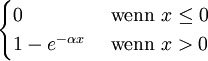
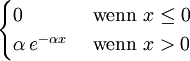
Erlang-Verteilung Eα,n 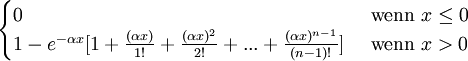
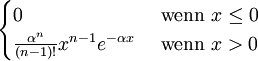
Normalverteilung 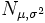
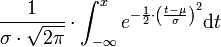
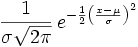
Logarithmische Normalverteilung 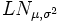
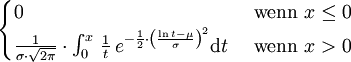
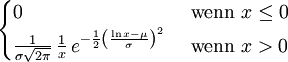
Weibull-Verteilung Wμ,σ,λ 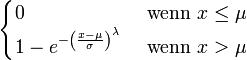
Chi-Quadrat-Verteilung Ck 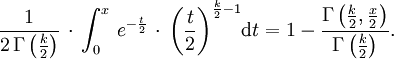
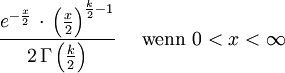
Students t-Verteilung Tk 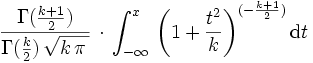
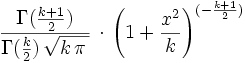
Fisher-Verteilung Fm,n 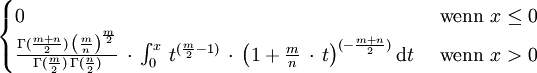
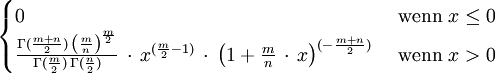
Gammaverteilung Gb,p 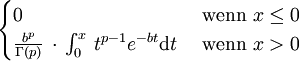
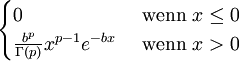
Erwartungswert, Varianz
Die für jede Verteilung charakteristischen Parameter Erwartungswert und Varianz ergeben sich aus der Dichtefunktion der jeweiligen Verteilung. Näheres zur anschaulichen Bedeutung und Herleitung in den entsprechenden Artikeln. Nachfolgend eine Auflistung dieser Größen, soweit berechenbar, für diskrete und stetige Verteilungen.
Diskrete Verteilungen
-
Verteilung P(X = k) Erwartungswert Varianz Bernoulli-Verteilung (Null-Eins-Verteilung) 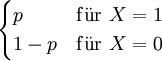
p p(1 − p) Binomialverteilung 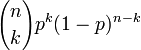
np np(1 − p) - negative Binomialverteilung (Pascal-Verteilung) 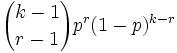
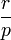
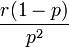
Geometrische Verteilung - Variante A p(1 − p)k − 1 für 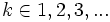
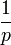
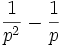
- Variante B p(1 − p)kfür 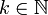
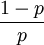
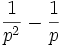
Diskrete Gleichverteilung 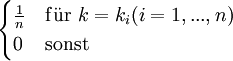
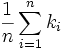
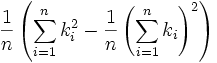
Diskrete Gleichverteilung auf 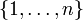
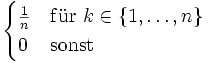
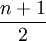
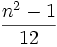
Hypergeometrische Verteilung 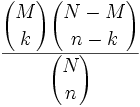
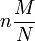
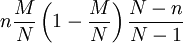
Logarithmische Verteilung 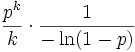
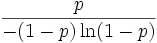
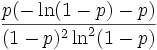
Multinomialverteilung (Polynomialverteilung) Panjer-Verteilung 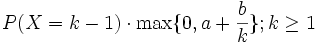
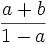
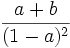
Poisson-Verteilung 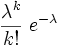
λ λ - Gemischte Poisson-Verteilung - Verallgemeinerte Poisson-Verteilung Zipf-Verteilung (Zeta-Verteilung) 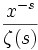
Stetige Verteilungen
-
Verteilung Kurzzeichen Vtlg. von X
Erwartungswert Varianz Gleichverteilung La,b 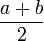
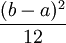
Exponentialverteilung Eα 
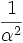
Erlang-Verteilung Eα,n 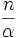
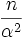
Normalverteilung 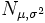
μ σ2 Logarithmische Normalverteilung 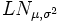
exp(μ + σ2 / 2) 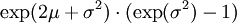
Weibull Verteilung Wμ,σ,λ 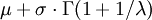
![\sigma^2\cdot[\Gamma(1+2/\lambda)-(\Gamma(1+1/\lambda))^2]](/pictures/dewiki/51/38ae32a8e8f1f24ad40d6187c0fe6c63.png)
Chi-Quadrat Verteilung Ck k 2k Studentverteilung Tk 0 (für k>1) 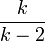 (für k>2)
(für k>2)Fisherverteilung Fm,n 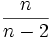 (für n>2)
(für n>2)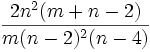 (für n>4)
(für n>4)Gammaverteilung Gb,p 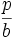
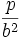
Beziehungen zwischen den Verteilungen
-
Beschreibung Merkhilfe *) Das Quadrat einer standardnormalverteilten Zufallsvariable ist Chi-Quadrat-verteilt mit Parameter 1. 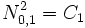
Die Summe unabhängiger Chi-Quadrat-verteilter Zufallsvariabler ist wieder Chi-Quadrat-verteilt. Ck + Cl = Ck + l Die Summe unabhängiger normalverteilter Zufallsvariabler ist wieder normalverteilt. 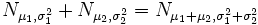
Die Summe unabhängiger poissonverteilter Zufallsvariabler ist wieder poissonverteilt. Pα + Pβ = Pα + β Die Summe unabhängiger binomialverteilter Zufallsvariabler mit gleichem Parameter p ist wieder binomialverteilt. Bm,p + Bn,p = Bm + n,p Die Summe unabhängiger negativbinomialverteilter Zufallsvariabler mit gleichem Parameter p ist wieder negativbinomialverteilt. NBm,p + NBn,p = NBm + n,p Die Summe unabhängiger erlangverteilter Zufallsvariabler mit gleichem Parameter α ist wieder erlangverteilt. Eα,m + Eα,n = Eα,m + n Die Summe unabhängiger gammaverteilter Zufallsvariabler mit gleichem Parameter b ist wieder gammaverteilt. Gb,p1 + Gb,p2 = Gb,(p1 + p2) Zusammenhang zwischen Erlangverteilung und Exponentialverteilung. Eα,1 = Eα Zusammenhang zwischen Erlangverteilung und Chi-Quadrat Verteilung. 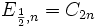
Zusammenhang zwischen Erlangverteilung und Gammaverteilung. (Für ganzzahligen zweiten Parameter stimmt die Gammaverteilung mit der Erlangverteilung überein.)
Eα,n = Gα,n Zusammenhang zwischen Weibull Verteilung und Exponentialverteilung. 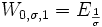
Sind X und Y unabhängige Zufallsvariable, X standardnormalverteilt und Y Ck-verteilt, dann ist 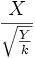 Tk-verteilt.
Tk-verteilt.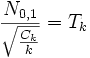
Sind X und Y unabhängige Zufallsvariable, X Cm-verteilt und Y Cn-verteilt, dann ist 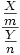 Fm,n-verteilt.
Fm,n-verteilt.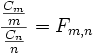
Der Logarithmus einer logarithmischnormalverteilten Zufallsvariablen ist normalverteilt. 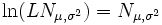
Ist Z negativbinomialverteilt mit Parameter 1 und p, so ist Z-1 geometrisch verteilt mit Parameter p. NB1,p − 1 = Gp
*) In der Merkhilfe steht zum Beispiel Ck nicht für die Chi-Quadrat Verteilung, sondern für eine Zufallsvariable in Chi-Quadrat Verteilung. Der Unterschied liegt darin, dass etwa die Verteilung der Summe von Zufallsvariablen (sie wird als Faltung der Verteilungen bezeichnet) üblicherweise mit zum Beispiel Ck * Cl (Ck,Cl Verteilungen) angeschrieben wird anstatt wie hier mit Ck + Cl (Ck,Cl Zufallsvariable). Der Vorteil der Schreibweise Ck * Cl (Ck,Cl Verteilungen) liegt darin, dass sie schon andeutet, welche Operation auf die Verteilungsfunktionen anzuwenden ist, um die Verteilung der Summe zu erhalten. Der Vorteil der Schreibweise Ck + Cl (Ck,Cl Zufallsvariable) liegt darin, dass sie angibt, welche Operation ursprünglich auf die Zufallsvariable gewirkt hat.
Das Zeichen „=“ steht für „hat gleiche Verteilung wie“.
Diejenigen Zufallsvariablen, die auf der linken Seite des Gleichheitszeichens stehen, seien stets vollständig unabhängig voneinander.
Aus den oben angeführten Regeln folgt zum Beispiel (in „Merkhilfe“-Notation):
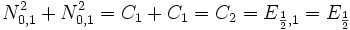 . Man beachte, dass dabei die erste Zufallsvariable
. Man beachte, dass dabei die erste Zufallsvariable 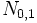 von der zweiten Zufallsvariablen
von der zweiten Zufallsvariablen 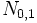 unabhängig sein muss. Wenn man stattdessen beide Male dieselbe Zufallsvariable verwendet, wenn man also
unabhängig sein muss. Wenn man stattdessen beide Male dieselbe Zufallsvariable verwendet, wenn man also 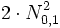 berechnet, ist das Ergebnis ein anderes!
berechnet, ist das Ergebnis ein anderes!Weblinks
-
Wikimedia Foundation.
