Stufenwinkelsatz

Stufenwinkelsatz: α = β

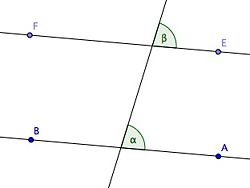
Der Stufenwinkelsatz ist ein mathematischer Satz. Er besagt: Wenn zwei parallele Geraden a und b von einer dritten Geraden c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß.

Der Stufenwinkelsatz ist umkehrbar, d. h. es gilt: Werden zwei Geraden a und b von einer dritten Geraden c geschnitten und die Stufenwinkel sind gleich groß, so sind a und b parallel.

Beweis

Beweis durch Widerspruch: α und β sind die Stufenwinkel

Bewiesen wird die Umkehrung des Stufenwinkelsatzes, woraus der Beweis für den Stufenwinkelsatz selbst folgt.

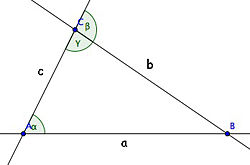
Seien dazu a und b zwei Geraden und schneide die Gerade c die Gerade a im Punkt A und die Gerade b im Punkt C. Weiterhin seien die als Stufenwinkel bezeichneten WInkel α und β gleich groß.

Annahme des Widerspruchsbeweises: a und b sind nicht parallel. Folge:

Es existiert also ein Schnittpunkt B der Geraden a und b, sodass ein Dreieck ABC existiert. Nach dem Nebenwinkelsatz ist der Innenwinkel von C = γ = 180° - β. Dann ist

γ + α = 180° - β + α = 180°, da nach Voraussetzung β = α

Daraus folgt für den Innenwinkel δ am Punkt B des Dreieck ABC:

δ = 180° - (γ + α) = 180° - 180° = 0°.

Das heißt jedoch, dass gar kein Schnittpunkt von den Geraden a und b existiert; Widerspruch zur Annahme, was zu beweisen war.

Literatur

• Hans Schupp: Elementargeometrie. Schöningh, Hannover 1977, ISBN 3-506-99189-2.