- Summensymbol
-
Dieser Artikel befasst sich in erster Linie mit der Summe als dem Ergebnis einer Addition. In der Mengenlehre wird der Begriff auch als eine ältere Bezeichnung für die Vereinigungsmenge benutzt. Ferner siehe auch direkte Summe. - 2 + 3
- 4 + 7 + 1
- 4 + 7 + 1 = 7 + 4 + 1
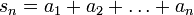
- an = n2.
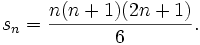
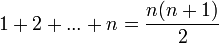
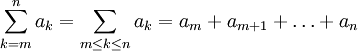
- einfaches Beispiel:
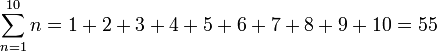
- Entweder wird unten ein Start- und oben ein Endwert angegeben (hier: m und n). Der Laufindex wird in der Regel nur unten angeschrieben; ausführlicher, aber recht ungebräuchlich, ist
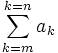
- oder es werden unten eine oder mehrere Bedingungen für die Zählvariable angegeben (hier:
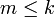und 
). 
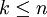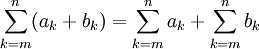
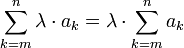
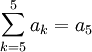
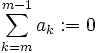
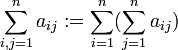
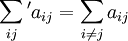
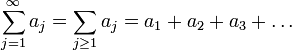
![\sum_{k>0} \left[\frac{n}{p^k}\right] = \left[\frac{n}{p}\right] + \left[\frac{n}{p^2}\right] + \left[\frac{n}{p^3}\right] + \dots](/pictures/dewiki/56/8a4437a2581c5db8781abd05af6aee61.png)
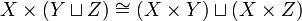
Inhaltsverzeichnis |
Wortgeschichte und -bedeutungen
Das Wort Summe wurde im Mittelhochdeutschen vom lateinischen summa entlehnt. Summa war bis in das 19. Jahrhundert neben Summe gebräuchlich. Das lateinische summa geht auf summus zurück, einen der Superlative zu superus, superior, der das Oberste, Höchste, Größte bezeichnet. „Das Oberste“ deshalb, weil die Römer die Summe in der obersten Zeile (also über den Summanden) zu notieren pflegten und nicht, wie heute üblich, „unterm Strich“.
Im weiteren Sinne bezeichnet Summe eine Gemeinheit oder einen Inbegriff.
In der Alltagssprache bezeichnet Summe einen Geldbetrag, unabhängig davon, ob er durch Addition zustande gekommen ist.
Summe als Ergebnis einer Addition
In dem mathematischen Term
heißen die Zahlen 2 und 3 Summanden. Der gesamte Term wird als die „Summe von 2 und 3“ bezeichnet.
Man kann eine Summe von mehr als zwei Summanden bilden, so zum Beispiel
Aufgrund der Assoziativität der Addition muss dabei nicht angegeben werden, in welcher Reihenfolge die Additionen auszuführen sind. So gilt, dass (4 + 7) + 1 = 4 + (7 + 1) ist und die Summe auch ohne Klammern geschrieben werden kann.
Aufgrund des Kommutativgesetzes der Addition ist auch die Reihenfolge der Summanden egal, d. h. es ist zum Beispiel
Wird n-mal die gleiche Zahl a addiert, dann kann die Summe auch als Produkt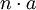 
geschrieben werden.
Summe einer Folge, Reihe
Wenn eine Summe sehr viele Summanden hat, ist es zweckmäßig, eine abgekürzte Schreibweise zu vereinbaren. Die Summe der ersten 100 natürlichen Zahlen kann zum Beispiel als
angegeben werden, denn es ist leicht zu erraten, welche Summanden durch die Auslassungspunkte ersetzt wurden.
So wie man in der elementaren Arithmetik von Zahlenrechnungen wie 2 + 3 = 5 zu Buchstabenrechnungen wie 2 + x = y übergeht, so kann man z.B. die Summe von hundert ganz bestimmten Zahlen zur Summe einer beliebigen Anzahl beliebiger Zahlen verallgemeinern. Dazu wird zunächst eine Variable gewählt, zum Beispiel n, die die Anzahl der Summanden bezeichnet. Im obigen Fall, der Summe der ersten einhundert natürlichen Zahlen, wäre n = 100. Da beliebig große n zugelassen sein sollen, ist es nicht möglich, alle n Summanden durch n verschiedene Buchstaben zu bezeichnen. Stattdessen wird ein einzelner Buchstaben z.B. a gewählt und um einen Index ergänzt. Dieser Index nimmt nacheinander die Werte 1, 2,… an. Die Summanden heißen dementsprechend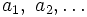 
. Die Summanden bilden somit eine Zahlenfolge (siehe Folge (Mathematik)).
Wir können nun für beliebige natürliche Zahlen n die Summe der ersten n Glieder der Zahlenfolge als
schreiben. Wenn man für n verschiedene Werte 1, 2, ... einsetzt, bilden die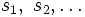 
ihrerseits ebenfalls eine Folge. Eine solche Folge von Partialsummen über die Anfangsglieder einer Folge wird als Reihe bezeichnet.
Beispiel: Für die Folge der Quadratzahlen ist a1 = 1, a2 = 4, a3 = 9. Ganz allgemein gilt
Die Reihe der Partialsummen dieser Folge beginnt mit s1 = 1 , s2 = 5, s3 = 14. Eine Summationsformel besagt nun für beliebige n
Weitere Summationsformeln wie zum Beispiel Der kleine Gauß
finden sich in der Formelsammlung Algebra. Der Beweis solcher Formeln erfolgt über vollständige Induktion.
Notation mit dem Summenzeichen
Summen über endliche oder unendliche Reihen können statt mit Auslassungspunkten auch mit dem Summenzeichen notiert werden:
Das Summenzeichen besteht aus dem großen griechischen Buchstaben Sigma, gefolgt von einem Folgenglied, das durch einen zuvor nicht benutzten Index (hier k) bezeichnet wird. Dieser Index wird oft als Laufindex oder Summationsvariable bzw. Lauf- oder Zählvariable bezeichnet. Hierfür werden meistens die Buchstaben i, j und k verwendet. Wenn nicht eindeutig hervorgeht, welche Variable die Zählvariable ist, muss dieses im Text angemerkt werden.
Welche Werte die Laufvariable annehmen kann, wird an der Unterseite, gegebenenfalls auch der Oberseite des Σ angezeigt. Es gibt dafür zwei Möglichkeiten:
Diese Angaben können reduziert oder weggelassen werden, wenn angenommen werden kann, dass der Leser sie aus dem Kontext heraus zu ergänzen vermag.
Hiervon wird in bestimmten Zusammenhängen ausführlich Gebrauch gemacht: In der Tensorrechnung vereinbart man häufig die einsteinsche Summationskonvention, der zufolge sogar das Summationszeichen weggelassen werden kann, da aus dem Kontext klar ist, dass über alle doppelt vorkommenden Indizes zu summieren ist.
Klammerkonventionen und Rechenregeln
Wird das Folgeglied als Summe (oder Differenz) mitgeteilt, so muss es in Klammern geschrieben werden:
Wird das Folgeglied als Produkt (oder Quotient) mitgeteilt, so ist die Klammer überflüssig:
Vorsicht: Allgemein gilt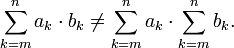 
Ausgeartete Summen
Für m = n besteht die Summe aus einem einzigen Summanden an:
Ferner hat es sich als nützlich erwiesen, für n = m − 1 eine leere Summe zu definieren:
Man beachte, dass dieses der einzige Fall mit n < m ist, der sinnvoll definiert werden kann. Im Gegensatz zur Integralnotation bleibt die Summe für n<m in allen anderen Fällen undefiniert.
Doppelsummen
Auch über Summen kann wieder summiert werden. Dieses ist insbesondere sinnvoll, wenn die erste, die „innere“ Summe, wiederum einen Index enthält, der als Laufindex für die „äußere“ Summe verwendet werden kann. Man schreibt zum Beispiel:
Dabei gilt die Regel: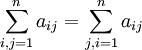 
In der mathematischen Physik gilt für Doppelsummen zudem folgende Konvention:
Ein Apostroph am Summenzeichen besagt, dass bei der Summation Summanden auszulassen sind, für die die beiden Laufvariablen übereinstimmen:
Unendliche Summen
Wenn unendlich viele Ausdrücke summiert werden, also zum Beispiel
mit unendlich vielen Summanden ungleich null, müssen Methoden der Analysis angewendet werden, um den entsprechenden Grenzwert zu finden. Eine solche Summe wird unendliche Reihe genannt. Als Obergrenze schreibt man das Symbol für Unendlichkeit (
). Siehe dazu den Artikel Reihe (Mathematik).
Es ist aber anzumerken, dass nicht jede Summe, die ∞ als Obergrenze besitzt, eine unendliche Summe sein muss. Zum Beispiel hat die Summe
für Primzahlen p und der Ganzzahl-Funktion [x], zwar unendlich viele Summanden, aber nur endlich viele sind ungleich null. (Diese Summe gibt an, wie oft der Faktor p in der Primfaktorzerlegung von n! vorkommt.)
Verwandte Begriffe
Die disjunkte Vereinigung von Mengen hat eine gewisse formale Ähnlichkeit mit der Addition von Zahlen; sind beispielsweise X und Y endliche Mengen, so ist die Anzahl der Elemente von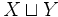 
gleich der Summe der Elementanzahlen von X und Y. Das kartesische Produkt ist distributiv über dieser Summenbildung:
Die aus kategorieller Sicht analoge Konstruktion für Vektorräume oder abelsche Gruppen wird als direkte Summe bezeichnet; allgemein spricht man von einem Koprodukt.
Eine Teleskopsumme ist in der Mathematik eine endliche Summe von Differenzen, bei der je zwei Nachbarglieder (außer dem ersten und dem letzten) sich gegenseitig aufheben.
Weblinks
Wikimedia Foundation.
