Teilfolgen

In der Mathematik ist eine Teilfolge einer unendlichen Folge eine neue Folge, die entsteht, wenn Folgenglieder von der ursprünglichen Folge weggelassen werden. Es können endlich viele Glieder (insbesondere auch gar keine) oder unendlich viele weggelassen werden. Sofern nicht ausdrücklich von einer endlichen Teilfolge gesprochen wird, ist üblicherweise wieder eine unendliche Folge gemeint.

Eine Teilfolge kann aus der Folge (a_n) gebildet werden, indem nur die Elemente 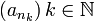$(a_{n_k})\,{k \in \mathbb{N}}$ berücksichtigt werden, wobei n₁ < n₂ < n₃ < ... eine streng monoton wachsende unendliche Folge ist.

(a_n) ist selbst auch eine Teilfolge von (a_n).

Beispiele

• Folge: a_n = ( − 1)ⁿ. Teilfolge mit n_k = 2k: $(a_{n_k})=(1,1,1,...)$
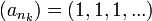
• Folge: a_n = n. Teilfolge mit n_k = k²: $(a_{n_k})=(1,4,9,16,...)$

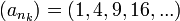
Folgenkompakter Raum

Nach dem Satz von Bolzano-Weierstraß besitzt jede beschränkte unendliche reelle Zahlenfolge mindestens eine konvergente Teilfolge. Allgemein heißt ein topologischer Raum folgenkompakt, wenn er die Eigenschaft hat, dass jede Folge mindestens eine konvergente Teilfolge hat.

Konvergenz

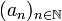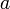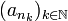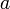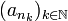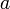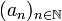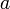Ist eine Folge $(a_n)_{n\in\N}\;$ konvergent gegen $a\;$, so konvergiert auch jede Teilfolge $(a_{n_k})_{k\in\N}\;$ gegen denselben Grenzwert $a\;$. Umgekehrt gilt auch, wenn jede Teilfolge $(a_{n_k})_{k\in\N}\;$ gegen denselben Grenzwert $a\;$ konvergiert, dass auch die Folge $(a_n)_{n\in\N}\;$ gegen $a\;$ konvergiert.

In jedem topologischen Raum gilt sogar der Satz, dass eine Folge 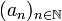$(a_n)_{n\in\N}\;$ genau dann gegen 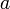$a\;$ konvergiert, wenn jede Teilfolge 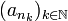$(a_{n_k})_{k\in\N}\;$ eine Teilteilfolge 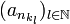$(a_{n_{k_l}})_{l\in\N}\;$ enthält, die gegen 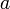$a\;$ konvergiert. Die Bedeutung dieses Satzes liegt erstens darin, dass er bei vielen Konvergenzbeweisen in folgenkompakten Räumen hilfreich ist. Zweitens liefert dieser Satz ein Kriterium, ob ein Konvergenzbegriff durch eine Topologie beschrieben werden kann; die punktweise Konvergenz fast überall einer Funktionenfolge erfüllt beispielsweise nicht diesen Satz und kann daher nicht durch eine Topologie beschrieben werden.