Satz von Bolzano-Weierstrass

Der Satz von Bolzano-Weierstraß (nach Bernhard Bolzano und Karl Weierstraß) ist ein Satz der Analysis. Er lautet:

Erste Fassung:

Jede beschränkte Folge komplexer Zahlen (mit unendlich vielen Gliedern) enthält (mindestens) eine konvergente Teilfolge.

Zweite Fassung:

Jede beschränkte Folge komplexer Zahlen (mit unendlich vielen Gliedern) hat (mindestens) einen Häufungspunkt. Jede beschränkte Folge reeller Zahlen hat einen größten und einen kleinsten Häufungspunkt.

Beweisskizze

Beim Beweis des Satzes für beschränkte reelle Zahlenfolgen geht man in der Regel wie folgt vor:

1. Beginne mit dem Intervall $I = [-L,\,L]$, das alle Folgeglieder enthält. Wähle a₁ als erstes Glied der zu bestimmenden Teilfolge.
2. Halbiere das Intervall (der Mittelpunkt des Intervalls wird dabei beliebig einem der beiden Teilintervalle zugeschlagen); mindestens eine Hälfte muss unendlich viele Folgenglieder enthalten, diese Hälfte werde nun mit I bezeichnet. Wähle als nächstes Glied der Teilfolge das erste Element a_n, das in I liegt und dessen Index größer ist als der des zuvor gewählten Elements.
3. Fahre mit dem vorigen Punkt unendlich lange fort. Das betrachtete Intervall wird dabei immer kleiner, so dass die Teilfolge gegen den einzigen Punkt konvergiert, der in allen Intervallen liegt. Dieser existiert als gemeinsamer Punkt einer Intervallschachtelung.

Verallgemeinerungen

Um den größten Häufungspunkt zu bestimmen, muss man, wann immer möglich, das obere Teilintervall wählen, für den kleinsten Häufungspunkt das untere Teilintervall.

Die komplexen Zahlen werden im Kontext dieses Satzes als zweidimensionaler reeller Vektorraum betrachtet. Für eine Folge 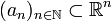$(a_n)_{n\in\N}\subset\R^n$ von Spaltenvektoren mit n reellen Komponenten wählt man zuerst eine Teilfolge, die in der ersten Komponente konvergiert. Von dieser wählt man wieder eine Teilfolge, die auch in der zweiten Komponente konvergiert. Die Konvergenz in der ersten Komponente bleibt erhalten, da Teilfolgen konvergenter Folgen wieder konvergent mit demselben Grenzwert sind. Und so weiter, bis die n-te Teilfolge auch in der letzten Komponente konvergiert.

Man kann mittels Cantors Diagonaltrick auch Folgen von abzählbar unendlich-dimensionalen Vektoren betrachten, die also ihrerseits wieder reelle Zahlenfolgen sind bzw. durch solche dargestellt werden können. Dabei konstruiert man sich Teilfolgen 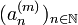$(a^{(m)}_{n})_{n\in\N}$, m=1,2,..., die jeweils Teilfolgen der zuvor konstruierten Teilfolgen sind und in den ersten m Komponenten konvergieren. Zum Schluss kann man zeigen, dass die Diagonalfolge 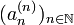$(a^{(n)}_{n})_{n\in\N}$ in allen der unendlich vielen Komponenten konvergiert.

Folgerungen

Aus dem Satz von Bolzano-Weierstraß folgt, dass jede monotone und beschränkte Folge reeller Zahlen konvergiert und dass eine stetige Funktion auf einem abgeschlossenen und beschränkten Intervall ein Maximum bzw. ein Minimum annimmt.

Der Satz von Bolzano-Weierstraß ist eng verwandt mit dem Satz von Heine-Borel. Eine Verallgemeinerung beider Sätze auf topologische Räume ist folgender: Ein topologischer Raum ist genau dann kompakt, wenn jedes Netz ein konvergentes Teilnetz hat.

Weblinks