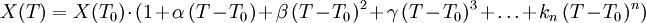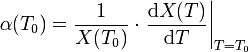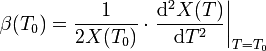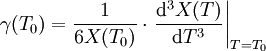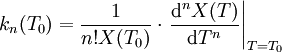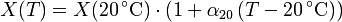Temperaturbeiwert

Der Temperaturkoeffizient (deutsch:Temperaturbeiwert) beschreibt die relative Änderung einer physikalischen Größe in Abhängigkeit von der Änderung der Temperatur gegenüber einer Bezugstemperatur.

Temperaturkoeffizienten gibt es für die Länge, das Volumen (siehe Ausdehnungskoeffizient), den Druck, den elektrischen Widerstand, Temperaturspannung der Halbleiterdiode und andere Größen. Ein linearer Zusammenhang liegt im allgemeinen nur in einem begrenzten Temperaturintervall vor.

Grundlagen

Die Temperaturabhängigkeit einer physikalischen Größe ist im allgemeinen nichtlinear und kann durch ein Taylorpolynom n-ten Grades (siehe Taylorreihe) der Form

$X(T) = X(T_0) \cdot (1 + \alpha\,(T-T_0) + \beta\,(T-T_0)^2 + \gamma\,(T-T_0)^3 + \dots + k_n\,(T-T_0)^n)$

angenähert werden. Dabei bedeuten

• X = temperaturabhängige physikalische Größe
• T = Temperatur
• T₀ = Bezugstemperatur, meist 20 °C
• α = Temperaturkoeffizient 1. Ordnung
• β = Temperaturkoeffizient 2. Ordnung
• γ = Temperaturkoeffizient 3. Ordnung
• k_n = Temperaturkoeffizient n-ter Ordnung

Die Temperaturkoeffizienten können wie folgt berechnet werden:

$\alpha(T_0) = \frac{1}{X(T_0)} \cdot \left.\frac{\mathrm{d}X(T)}{\mathrm{d}T}\right|_{T=T_0}$

$\beta(T_0) = \frac{1}{2X(T_0)} \cdot \left.\frac{\mathrm{d}^2X(T)}{\mathrm{d}T^2}\right|_{T=T_0}$

$\gamma(T_0) = \frac{1}{6X(T_0)} \cdot \left.\frac{\mathrm{d}^3X(T)}{\mathrm{d}T^3}\right|_{T=T_0}$

$k_n(T_0) = \frac{1}{n!X(T_0)} \cdot \left.\frac{\mathrm{d}^nX(T)}{\mathrm{d}T^n}\right|_{T=T_0}$

Es ist zu beachten, dass die Temperaturkoeffizienten von der Bezugstemperatur abhängen. Je stärker die Temperaturabhängigkeitskennlinie von einer Geraden abweicht und je stärker die Temperatur von der Bezugstemperatur abweicht, desto mehr Temperaturkoeffizienten höherer Ordnung sind erforderlich, um den Näherungsfehler klein zu halten.

Für viele Anwendungen können die Temperaturkoeffizenten höherer Ordnungen vernachlässigt werden. Außerdem wird als Bezugstemperatur oft 20 °C gewählt. Man nutzt dann eine einfache Linearisierung der Kennlinie um die Bezugstemperatur:

$X(T) = X(20\,^{\circ}\mathrm{C}) \cdot (1 + \alpha_{20}\,(T-20\,^{\circ}\mathrm{C}))$

In vielen Fällen muss die Kennlinie nicht nur in einem breiten Temperaturbereich linearisiert werden, sie muss auch so umgewandelt werden, dass man die Temperatur T als Ergebnis erhält, wenn X(T) – beispielsweise der Widerstand eines Pt100 – bekannt ist. Beides erfordert oft aufwendigere Methoden.

Die Nichtlinearität der Temperaturabhängigkeit ist besonders bei der Entwicklung von empfindlichen Sensoren zu beachten. Da aber meist lineare Kennlinien gewünscht werden, nutzt man Brücken- und Differenzschaltungen, um zumindest die Koeffizienten mit dem größten nichtlinearen Einfluss auf die Kennlinie (die 2. Ordnung) zu unterdrücken.

Beispiele

Temperaturkoeffizienten beim idealen Gas

Für das ideale Gas sind die Temperaturkoeffizienten für Druckänderung und Volumenänderung gleich $\tfrac{1}{273,15} K^{-1}$.

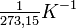Durch die idealisierenden Annahmen sind Druckänderung und Volumenänderung linear.

Temperaturkoeffizient des elektrischen Widerstands

Die Temperaturabhängigkeit des elektrischen Widerstands und damit der Bauelemente (Leitungen, Widerstände) muss bei der Konstruktion von Baugruppen und der Auslegung von Schaltungen immer einkalkuliert werden. Andererseits wird diese Eigenschaft auch genutzt, z. B. bei Widerstandsthermometern.

Da der Temperaturkoeffizient des elektrischen Widerstands nicht linear ist, gibt es zum Beispiel für das standardisierte Widerstandsthermometer Pt100 Polynome zur Berechnung der absoluten Temperatur aus dem gemessenen Widerstand. Die Herleitung dieser Formeln wird in Linearisierung beschrieben. Oft wird 0 °C oder 25 °C als Bezugstemperatur gewählt und nicht 20 °C.

Wie oben bereits erwähnt, sind oft lineare Funktionen, zum Beispiel für regelungstechnische Anwendungen, erwünscht. Dieser lineare Temperaturkoeffizient α gibt die relative Änderung des Widerstandswertes pro 1 Kelvin Temperaturunterschied zum Bezugspunkt an. Bei den in der Elektrotechnik wichtigen Leitermaterialien Kupfer und Aluminium kann im Temperaturbereich 0 bis 50 °C für Abschätzungen mit dem Wert 0,4 % pro Kelvin gerechnet werden.

Lineare Widerstands-Temperaturkoeffizienten einiger Stoffe bei 20 °C

Reine Metalle	α in K−1	Legierungen	α in K−1	Nichtmetalle	α in K−1
Aluminium (99,5 %)	4,0 · 10−3	Aldrey (AlMgSi)	3,6 · 10−3	Kohlenstoff	−0,5 · 10−3 [1]
Blei	4,22 · 10−3	Berylliumbronze (SnBe4Pb)	0,5 · 10−3	Graphit	−0,2 · 10−3
Eisen (rein)	6,57 · 10−3 [2]	Manganin (Cu84Ni4Mn12)	±0,04 · 10−3	Lichtbogen-Kohle	0,5 · 10−3 [3]
Gold	3,98 · 10−3	Konstantan	0,01 · 10−3	Germanium	−48 · 10−3 [1]
Kupfer (99,9 %)	3,9 · 10−3	Messing (CuZn37)	1,3 · 10−3	Silizium	−75 · 10−3 [1]
Nickel	6,7 · 10−3	Nickelin (CuNi30Mn)	0,15 · 10−3
Platin	3,88 · 10−3	Weicheisen (4 % Si)	0,9 · 10−3 [3]
Quecksilber	0,9 · 10−3	Stahl C15	5,7 · 10−3
Silber	3,8 · 10−3
Tantal	3,5 · 10−3
Wolfram	4,8 · 10−3

Einzelnachweise

1. ↑ ^{a b c} http://www.physik.uni-mainz.de/exakt/aspect/sb_home/SpezWiderstand.html
2. ↑ Tabellenbuch Elektrotechnik. Europa Lehrmittel, Wuppertal 1966
3. ↑ ^{a b} H.H. Gobbin: Naturkonstanten. Wittwer, Stuttgart 1962