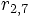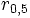Terminzinsgeschäft

Unter dem Terminzins (auch forward rate) versteht man den Zinssatz, welcher für Kapitalanlagen fällig wird, deren Laufzeit nicht sofort, sondern an einem bestimmten Zeitpunkt in der Zukunft beginnt und eine bestimmte Laufzeit hat. Es ist derjenige Zinssatz, der heute für eine Mittelanlage oder Kreditaufnahme im Zeitpunkt s für die Frist t-s vereinbart wird. Man spricht dann von einem Zinssatz s gegen t Monate, d. h. Mittelanlage erfolgt in s bis t.

Die Notierung des Terminzinssatzes ist üblicherweise wie folgt:

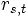$\ r_{s,t}$ oder $\ r(s,t)$

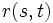
wobei

• s = Startzeit der Laufzeit
• t = Ende der Laufzeit.

So ist z. B.

$\ r_{2,7}$

der Zinssatz, der für eine fünfjährige Kapitalanlage gilt, die in zwei Jahren zu laufen beginnt.

Der Kassazins als Spezialfall des Terminzinses notiert wie folgt:

$\ r_{0,5}$

… was den Zinssatz bezeichnet, welcher für eine fünfjährige Kapitalanlage mit sofortigem Laufzeitbeginn gilt.

Bewertung durch Duplikation

Der Terminzins lässt sich aus den Kassazinsen zu verschiedenen Laufzeiten (Zinsstruktur) eindeutig berechnen. Die Terminzinssätze sind in der aktuellen Zinsstruktur (y_s und y_t implizit enthalten. Man nennt sie deshalb auch implizite Zinssätze. Grundlage der Berechnung ist das Prinzip der Arbitragefreiheit.

Beispiel:

• Ein Anleger legt heute Geld fest für 7 Jahre zu einem bestimmten Zinssatz an.
• Ein zweiter Anleger legt Geld erst in 5 Jahren an und macht mit der Bank heute schon einen Zinssatz aus, zu welchem er das Geld nach 5 Jahren für die nächsten 2 Jahre anlegt.

Zeitleiste
Zeitpunkt 0 (heute)	Mittelaufnahme in s	Rückzahlung in t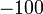
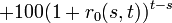
	$\ -100$	$\ +100(1+r_0(s,t))^{t-s}$

Der Zinssatz für eine Mittelaufnahme (hier: 100) von heute bis zum Zeitpunkt t muss gleich dem Produkt des Zinses von heute bis s und des Zinses von s bis t, also dem Terminzinssatz r₀(s,t) sein. Für beide Fälle muss der Barwert gleich sein.

$(1+r_0(s,t))^{t-s} \cdot (1+y_s)^s= (1+y_t)^t$

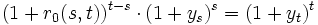
Daher ergibt sich folgende Formel:

$r_0(s,t)= \sqrt[t-s]{\frac{(1+y_t)^t}{(1+y_s)^s}}-1$

mit

• r₀(s,t) =Terminzinssatz
• y_t = Zinssatz von 0 bis t
• y_s = Zinssatz von 0 bis s
• t = Gesamtlaufzeit; Ende des Terminzinsgeschäfts
• s = Beginn der Terminzinsgeschäfts

Der Terminzinssatz wird synthetisch erzeugt (Duplikation).

alternativer Weg

Bestimmung der Terminzinssätze aus den Diskontfaktoren

$r_0(s,t) = \sqrt\frac{AF(0,s)}{AF(0,t)}-1$

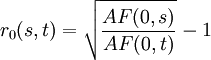
Ausgleichszahlung

Aus Sicht des Kreditnehmers ergibt sich folgende Zahlung:

$\frac{(E-r)A (T_2-T_1)}{1+E(T_2-T_1)}$

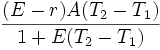
Die vorschüssige Zahlung reduziert das Ausfallrisiko, da Ausfälle des jeweiligen Kontrahenten nach der Zahlung nicht mehr ins Gewicht fallen.

Das verbleibende Kontrahentenrisiko besteht nur für die nächsten zwölf Monate zum Settlement des FRA.

Anwendung

In dem Fall einer Realisierung der Terminzinssätze in Periode s, gelten als Kassazinssätze folgende Werte: in Periode t der Zinssatz r₀(s,t) als Kassazinssatz.

Im Allgemeinen ist der Terminzinssatz nicht identisch mit dem Kassazinssatz in s für eine Mittelaufnahme bzw. Anlage bis t. Empirisch gesehen ist r_0(s,t) meist kein guter Schätzer für diesen zukünftigen Kassazinssatz.

Der einperiodige Terminzins r₀(0,1) ist gleich dem Kassazins für eine Periode.