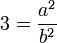- Theodorus-Konstante
-
Die Quadratwurzel aus 3 (geschrieben
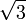 ) ist die positive, reelle Zahl, die mit sich selbst multipliziert 3 ergibt. Die Wurzel von 3 ist eine irrationale Zahl. Sie ist auch bekannt unter dem Namen Theodorus-Konstante, benannt nach Theodoros von Kyrene.
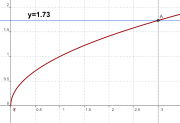
) ist die positive, reelle Zahl, die mit sich selbst multipliziert 3 ergibt. Die Wurzel von 3 ist eine irrationale Zahl. Sie ist auch bekannt unter dem Namen Theodorus-Konstante, benannt nach Theodoros von Kyrene.Näherungsweise gilt:
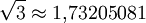
Ihre Kettenbruchentwicklung ist
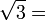 [1;1,2,1,2,1,2,1,2,1,2,…].
[1;1,2,1,2,1,2,1,2,1,2,…].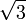 entspricht auch
entspricht auch 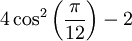 oder
oder 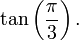
Inhaltsverzeichnis
Beweis der Irrationalität
Angenommen,
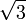 wäre rational. Dann könnte man die Zahl als Bruch zweier teilerfremder ganzer Zahlen a und b schreiben:
wäre rational. Dann könnte man die Zahl als Bruch zweier teilerfremder ganzer Zahlen a und b schreiben: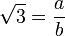 .
.
Durch Quadrieren der Gleichung erhält man
bzw.
- 3b2 = a2 (1)
In Gleichung (1) ist die rechte Seite genau dann ungerade, wenn a ungerade ist. Ebenso ist die linke Seite (weil 3 ungerade ist) genau dann ungerade, wenn b ungerade ist. Folglich haben a und b die gleiche Parität. Als teilerfremde Zahlen können aber nicht beide gerade sein, also sind a und b beide ungerade. Demnach kann man sie mit geeigneten ganzen Zahlen m und n in der Form
- a = 2m + 1 bzw. b = 2n + 1
schreiben. Setzt man diese Ausdrücke in (1) ein, ergibt sich
- 3(4n2 + 4n + 1) = 4m2 + 4m + 1
und nach elementaren Umformungen (Ausmultiplizieren, variable Ausdrücke auf eine Seite bringen, Division durch 2)
- 1 = 2(m2 + m − 3n2 − 3n) (2)
In Gleichung (2) ist die rechte Seite gerade, da sie das Doppelte einer ganzen Zahl ist, während die 1 links ungerade ist. Dies ist ein Widerspruch, so dass die Annahme,
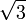 wäre rational, falsch sein muss. Folglich ist
wäre rational, falsch sein muss. Folglich ist 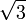 irrational.[1]
irrational.[1]Die ersten 100 Nachkommastellen
1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485756[2]
Anwendung
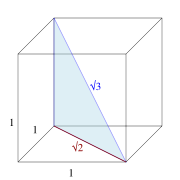
- Die Länge der Diagonale eines dreidimensionalen Würfels mit der Einheitslänge 1, beträgt
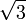
- Die Distanz zwischen zwei gegenüberliegenden Seiten eines regulären Sechsecks mit der Seitenlänge 1 beträgt
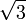
- Die Höhe eines gleichseitigen Dreiecks mit der Seitenlänge 1 beträgt
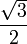
- Der Verkettungsfaktor, das Verhältnis von Phasenspannung (230 V) zu Außenleiterspannung (400 V), beträgt bei Dreiphasenwechselstrom
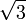
Weiterführende Links
Artikel
- Die Quadratwurzel von 2 ist die Länge der Quadratsdiagonale in der Ebene
- Die Quadratwurzel von 3 ist eine Mathematische Konstante
Quellen
Wikimedia Foundation.