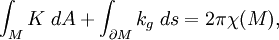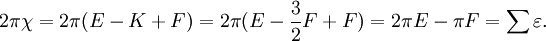Theorema elegantissimum

Der Satz von Gauß-Bonnet (nach Carl Friedrich Gauß und Pierre Ossian Bonnet) ist eine wichtige Aussage über Flächen, die ihre Geometrie mit ihrer Topologie verbindet, indem eine Beziehung zwischen Krümmung und Euler-Charakteristik hergestellt wird. Dieser Satz wurde unabhängig von beiden Mathematikern gefunden. Man beachte, dass auch französische Geometer ihn mit dem Namen von Gauß und Bonnet bezeichnen.

Definitionen und Satz

Sei M eine kompakte und orientierbare zweidimensionale riemannsche Mannigfaltigkeit mit Rand 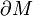$\partial M$. Bezeichne mit K die Gaußkrümmung in den Punkten von M und mit k_g die geodätische Krümmung der Randkurve 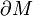$\partial M$. Dann gilt

$\int_M K\;dA+\int_{\partial M}k_g\;ds=2\pi\chi(M) ,$

wobei χ(M) die Euler-Charakteristik von M ist.

Der Satz kann im Besonderen auf Mannigfaltigkeiten ohne Rand angewendet werden. Dann fällt der Term 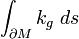$\int_{\partial M}k_g\;ds$ weg.

Erklärung des Satzes

Verzerrt man die Mannigfaltigkeit, so bleibt ihre Euler-Charakteristik unverändert, im Gegensatz zur Gaußkrümmung an den einzelnen Punkten. Der Satz sagt aus, dass das Integral über die Krümmung, also die Gesamtkrümmung, unverändert bleibt.

Beispiele

Die runde Sphäre M = S² mit Radius 1 hat in jedem Punkt die Gauß-Krümmung 1. Das Integral über die Gauß-Krümmung entspricht also ihrer Fläche, 4π. Andererseits ist die Euler-Charakteristik 2, da man die Sphäre als Verklebung von zwei (runden) Flächen entlang einer Kante mit einer Ecke bekommt (also 2-1+1=2).

Korollare

Theorema elegantissimum

Dieses von Gauß stammende Korollar besagt, dass die Gesamtkrümmung 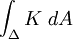$\int_{\Delta}K\;dA$ eines einfach zusammenhängenden geodätischen Dreiecks gleich dessen Winkelexzess ist. Für den Spezialfall der 2-Sphäre sieht man über die Außenwinkelsumme eines infinitesimalen (also flachen) Dreiecks von 5π die Äquivalenz zum Satz von Gauß-Bonnet. Die Äquivalenz gilt allerdings – im zweidimensionalen Fall – auch allgemein, was mithilfe einer Triangulierung eingesehen werden kann, denn für diese gilt:

$2\pi\chi=2\pi(E-K+F)=2\pi(E-\frac 32F+F)=2\pi E-\pi F=\sum\varepsilon.$

Verallgemeinerungen

Der Satz lässt sich auf n Dimensionen verallgemeinern. Man kann ihn ebenfalls auf simpliziale Flächen verallgemeinern, wobei man den Winkeldefekt einer Ecke als diskrete Gausskrümmung definiert.