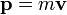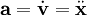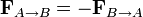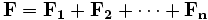Trägheitsgesetz

Newtons erstes und zweites Gesetz, in Latein, aus der Originalausgabe der Principia Mathematica von 1687.

Im Jahre 1687 erschien Isaac Newtons berühmtes Werk Philosophiae Naturalis Principia Mathematica (Mathematische Prinzipien der Naturphilosophie), in dem Newton drei Grundsätze (Gesetze) der Bewegung formuliert, die als die newtonschen Axiome, Grundgesetze der Bewegung, newtonsche Prinzipien oder auch newtonsche Gesetze bekannt sind. Sie werden in Newtons Werk mit Lex prima, Lex secunda und Lex tertia, insgesamt mit Axiomata, sive leges motus (‚Axiome, oder Gesetze der Bewegung‘), bezeichnet.

Diese Gesetze bilden das Fundament der klassischen Mechanik. Sie werden heute aber nicht mehr unbedingt als Axiome angesehen, weil sie sich als Folgerungen aus moderneren Grundsätzen, die über die klassische ‚newtonsche‘ Physik hinausgehen, ableiten lassen.

Erstes newtonsches Gesetz: Das Trägheitsprinzip („lex prima“)

Das erste Gesetz ist das Trägheitsprinzip. Es gilt nur in Inertialsystemen und wurde als erstes von Galileo Galilei im Jahre 1638 aufgestellt.

„Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen Translation, sofern er nicht durch einwirkende Kräfte zur Änderung seines Zustands gezwungen wird.“

Lateinischer Originaltext:

„Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.“^[1]

Die Geschwindigkeit 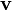$\mathbf v$ ist also unter der genannten Voraussetzung in Betrag und Richtung konstant. Eine Änderung des Bewegungszustandes kann nur durch Ausübung einer Kraft von außen erreicht werden, beispielsweise durch die Gravitationskraft.

In der klassischen Mechanik entspricht das erste newtonsche Gesetz den Gleichgewichtsbedingungen.

Zweites newtonsches Gesetz: Das Aktionsprinzip („lex secunda“)

Das zweite newtonsche Gesetz ist das Grundgesetz der Dynamik:

„Die Änderung der Bewegung einer Masse ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.“

Lateinischer Originaltext:

„Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.“

In den heutigen Begriffen entspricht die Kraft F der Änderung des Impulses p nach der Zeit:

$\mathbf F = {\dot \mathbf p}$,

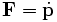wobei Newtons Formulierung genauer betrachtet das Zeitintegral auf beiden Seiten der Gleichung beinhaltet. Der Punkt über einem Buchstaben ist die von Newton eingeführte Notation für die zeitliche Änderung einer physikalischen Größe.

Für den Impuls selbst gilt

$\mathbf p = m \mathbf v$

Damit folgt für die Kraft mittels der Produktregel:

$\mathbf F = m \dot \mathbf v + \dot m \mathbf v$.

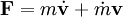Der zweite Summand enthält die zeitliche Änderung der Masse. Er ist nur für Systeme von Bedeutung, deren Masse sich während eines Prozesses ändert. Dies wäre etwa bei einem Regentropfen oder Schneekristall der Fall, der während seiner Entstehung an Masse zunimmt. Ein typisches Beispiel für ein System mit abnehmender Masse ist eine Rakete (siehe auch Raketengleichung). In solchen Fällen ist die Beschleunigung der Masse der wirkenden Kraft nicht proportional.

Für die meisten technischen Systeme ist die Masse m während der Bewegungsänderung konstant. Das zweite newtonsche Gesetz vereinfacht sich damit zu

$\mathbf F = m \mathbf a = m \ddot \mathbf x$,

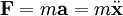wobei 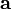$\mathbf a$ die Beschleunigung ist.

$\mathbf a = \dot \mathbf v = \ddot \mathbf x$

Mit dem zweiten Punkt über dem Buchstaben wird angedeutet, dass es sich um die Änderung der Änderung handelt. In dieser Form ist das Gesetz zuerst 1750 von Leonhard Euler formuliert worden^[2] und bildet die Grundlage beim Aufstellen der Bewegungs-Differentialgleichungen für zahlreiche Systeme der Mechanik.

Aus diesem Gesetz folgt direkt die Impulserhaltung. Ist die Beschleunigung gleich Null, so gilt offensichtlich für ein System mit konstanter Masse

$\mathbf F = \dot \mathbf p = 0$.

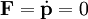Dies bedeutet, dass der Impuls sich nicht ändert und in Betrag und Richtung konstant bleibt.

Häufig wird der Ausdruck „Kraft = Masse mal Beschleunigung“ als zweites newtonsches Gesetz bezeichnet. Dies ist aber einerseits nicht korrekt, da dies nur für Systeme mit konstanter Masse gilt. Andererseits ist die Definition über den Impuls besser, da aus ihr direkt die Impulserhaltung folgt und sie weiterführend in gleicher Weise zum Kraftbegriff in der speziellen Relativitätstheorie führt (Viererkraft).

Im Originalwerk von Newton wurde, in modernen Begriffen ausgedrückt, bereits die allgemein gültige Formulierung „Kraft = Impulsänderung pro Zeit“ beschrieben. Dies gilt für Systeme mit konstanter oder veränderlicher Masse.

Drittes newtonsches Gesetz: Das Reaktionsprinzip („lex tertia“)

Das dritte Prinzip ist das Wechselwirkungsprinzip:

„Kräfte treten immer paarweise auf. Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio), so wirkt eine gleichgroße, aber entgegen gerichtete Kraft von Körper B auf Körper A (reactio).“

Lateinischer Originaltext: „Lex III. Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones is se mutuo semper esse aequales et in partes contrarias dirigi.“

$\mathbf {F}_{A \to B} = -\mathbf {F}_{B \to A}$

Das Wechselwirkungsprinzip wird auch als Prinzip von actio und reactio oder kurz „actio gleich reactio“ (lat. actio est reactio) bezeichnet.

Das Prinzip lässt sich auch so formulieren, dass in einem abgeschlossenen System die Summe der Kräfte verschwindet. Mit dem zweiten newtonschen Axiom ist das mit der Impulserhaltung äquivalent.

Superpositionsprinzip der Kräfte („lex quarta“)

In Newtons Werk wird das Prinzip der ungestörten Überlagerung oder Superpositionsprinzip der Mechanik als Zusatz zu den Bewegungsgesetzen beschrieben.

„Wirken auf einen Punkt (oder einen starren Körper) mehrere Kräfte 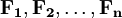$\mathbf {F_1},\mathbf {F_2}, \ldots, \mathbf {F_n}$, so addieren sich diese vektoriell zu einer resultierenden Kraft 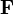$\mathbf {F}$ auf.“

$\mathbf {F} = \mathbf {F_1} + \mathbf {F_2} + \cdots + \mathbf {F_n}$

Später wurde dieses Superpositionsprinzip auch als Lex quarta bezeichnet.

Literatur

• Jerry Marion und Stephen Thornton: Classical Dynamics of Particles and Systems. Harcourt College Publishers, 1995, ISBN 0-03-097302-3.
• G. R. Fowles, G. L. Cassiday: Analytical Mechanics. Saunders College Publishing, 6. Auflage 1999, ISBN 0-03-022317-2.
• Ulrich Hoyer: Ist das zweite Newtonsche Bewegungsaxiom ein Naturgesetz? In: Zeitschrift für allgemeine Wissenschaftstheorie, Bd VIII, 1977, S. 292-301.

Einzelnachweise

1. ↑ Philosophiae naturalis principia mathematica. Bd. 1: Tomus Primus. London 1726, S. 13 (Digitalist) - fast ebenso in der Auflage Genf 1739, S. 20 (Digitalisat, 60 of 589): „Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.“
2. ↑ Euler: Découverte d'un nouveau principe de mécanique. Memoires de l´Academie royal des sciences, Berlin, Bd.6, 1752, S.185, Euler Opera Omnia, Serie 2, Bd.5, 1957