- Tschebyscheff-Ungleichung
-
In der Stochastik gibt die Tschebyschow-Ungleichung eine untere Grenze für die Wahrscheinlichkeit an, dass ein Wert einer Zufallsvariable mit endlicher Varianz innerhalb eines bestimmten Bereiches um den Erwartungswert der Variable liegt. Damit ist auch eine obere Grenze für die Wahrscheinlichkeit angegeben, dass die Werte außerhalb dieses Bereiches liegen. Der Satz lässt sich auch auf Verteilungen anwenden, die weder "glockenförmig" noch symmetrisch sind und setzt Grenzen dafür, wie viele der Daten "in der Mitte" liegen und wie viele nicht.
Die Tschebyschow-Ungleichung ist zu Ehren von Pafnuti Lwowitsch Tschebyschow benannt; in älteren Transkriptionen findet sich gelegentlich noch die Schreibweise Tschebyscheff oder Tschebyschev.
Inhaltsverzeichnis
Satz
Sei X eine Zufallsvariable mit Erwartungswert μ und endlicher Varianz σ2. Dann gilt für alle reellen Zahlen k > 0:
Durch Umstellen ergibt sich auch
Der Beweis ergibt sich als einfache Anwendung der Markow-Ungleichung.
Die von der Tschebyschow-Ungleichung angegebenen Grenzen können nicht nach oben verbessert werden. Man kann Zufallsvariablen konstruieren, für welche die Grenzen gleich den wirklichen Wahrscheinlichkeiten sind. Im Allgemeinen sind die Grenzen aber schwach. Eine quantitative Verbesserung liefert die Chernoff-Ungleichung.
Trotz der schwachen Grenzen kann der Satz nützlich sein, weil er ohne Verteilungsannahmen über die Zufallsvariablen auskommt, und somit wirklich für alle (insbesondere auch solche, die sich stark von der Normalverteilung unterscheiden) anwendbar ist. Außerdem sind die Schranken einfach zu berechnen.
Varianten
Abstand von Standardabweichung
Setzt man k = λσ mit λ > 0 als ein Vielfaches der Standardabweichung σ so erhält man eine oft zitierte Variante der Tschebyschow-Ungleichung:
Diese Ungleichung liefert nur für λ > 1 eine sinnvolle Abschätzung, für 0 < λ < = 1 ist sie trivial.
Verallgemeinerung auf höhere Momente
Die Tschebyschow-Ungleichung lässt sich auf höhere Momente verallgemeinern (Lit.: Ash, 1972, Theorem 2.4.9): Im Maßraum
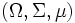 gilt für eine messbare Funktion
gilt für eine messbare Funktion 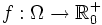 und
und 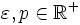
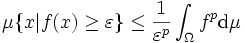 .
.
Das folgt sehr einfach aus
Anwendungen
- Der Satz wird beim Beweis des Gesetzes der großen Zahlen verwendet.
- Die Verallgemeinerung auf höhere Momente kann benutzt werden, um zu zeigen, dass aus der
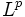 -Konvergenz von Funktionenfolgen die Konvergenz im Maß folgt.
-Konvergenz von Funktionenfolgen die Konvergenz im Maß folgt.
Beispiele
Beispiel 1
Nehmen wir zum Beispiel an, dass Wikipedia-Artikel im Durchschnitt 1000 Zeichen lang sind mit einer Standardabweichung von 200 Zeichen. Aus der Tschebyschow-Ungleichung kann man dann ableiten, dass mit mindestens 75% Wahrscheinlichkeit ein Wikipedia-Artikel eine Länge zwischen 600 und 1400 Zeichen hat (
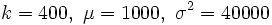 ).
).Der Wert für die Wahrscheinlichkeit wird auf folgende Weise berechnet:
Beispiel 2
Eine andere Folgerung aus dem Satz ist, dass für jede Wahrscheinlichkeitsverteilung mit Mittelwert μ und endlicher Standardabweichung σ mindestens die Hälfte der Werte im Intervall
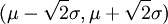 liegen (k2 = 2σ2).
liegen (k2 = 2σ2).Beispiel 3
Ein Zufallsereignis tritt bei einem Versuch mit Wahrscheinlichkeit
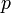 ein. Der Versuch wird
ein. Der Versuch wird 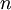 mal wiederholt; das Ereignis trete dabei
mal wiederholt; das Ereignis trete dabei 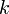 Mal auf.
Mal auf. 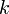 ist dann binomialverteilt und hat Erwartungswert
ist dann binomialverteilt und hat Erwartungswert 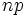 und Varianz
und Varianz 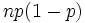 ; die relative Häufigkeit
; die relative Häufigkeit  des Eintretens hat somit Erwartungswert
des Eintretens hat somit Erwartungswert 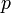 und Varianz
und Varianz 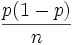 . Für die Abweichung der relativen Häufigkeit vom Erwartungswert liefert die Tschebyschow-Ungleichung
. Für die Abweichung der relativen Häufigkeit vom Erwartungswert liefert die Tschebyschow-Ungleichung![\operatorname{P}\left[\left|\frac{k}{n}-p \right|\geq \epsilon \right] \leq \frac{p(1-p)}{\epsilon^2n} \leq \frac{1}{4\epsilon^2n}](/pictures/dewiki/50/28b589a910096267e4af06d927d3765d.png) ,
,
wobei für die zweite Abschätzung die unmittelbar aus der Ungleichung vom arithmetischen und geometrischen Mittel folgende Beziehung
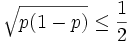 verwendet wurde.
verwendet wurde.Bei dieser Formel handelt es sich um den Spezialfall eines schwachen Gesetzes der großen Zahlen, das die stochastische Konvergenz der relativen Häufigkeiten gegen den Erwartungswert zeigt.
Literatur
- Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972, ISBN 0-12-065201-3.
- Ulrich Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 7. Auflage, Vieweg Verlag, Wiesbaden 2003, ISBN 3-528-67259-5.
- P. L. Tschebyschow (1867), On Mean Values , J. Math. Pures. Appl. 2(12), S. 177-184
Wikimedia Foundation.

![\operatorname{P}\left[\left|X-\mu\right|\geq k\right] \leq \frac{\sigma^2}{k^2} .](/pictures/dewiki/57/9cad70b1f50d37a935dd6b6510451f29.png)
![\operatorname{P}\left[\left|X-\mu\right| &lt; k\right] \geq 1 - \frac{\sigma^2}{k^2} .](/pictures/dewiki/98/b47e0d15a6f72eb19d3c62ddb0815c6a.png)
![\operatorname{P}\left[\left|X-\mu\right|\geq \lambda \sigma\right] \leq \frac{1}{\lambda^2} .](/pictures/dewiki/98/b891f459427b0162fa987d8b4845ea07.png)
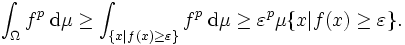
![\operatorname{P}\left[\left|X-1000\right| &lt; 400\right] \geq 1 - \frac{200^2}{400^2} = 0,75 \Rightarrow 75\%](/pictures/dewiki/55/72ea1267ec86011ef5bae7a6d7c0eaab.png)