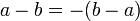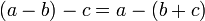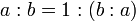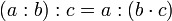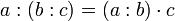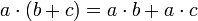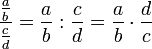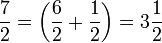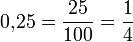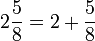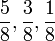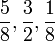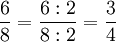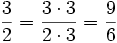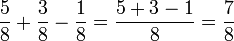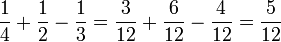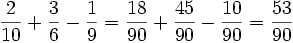- Unechter Bruch
-
Notation
Addition und Subtraktion sind sogen. Rechenoperationen der ersten Stufe. Multiplikation und Division sind sogen. Rechenoperationen der zweiten Stufe.
siehe auch Operatorrangfolge
Regeln
- Stehen Operationen in runden Klammern, so werden diese zuerst ausgeführt.
- Stehen Operationen der gleichen Stufe hintereinander, so werden die Operationen von links nach rechts ausgeführt.
Addieren
(Zusammenzählen)
Summand + Summand = Summe 3 + 4 = 7
Subtrahieren
(Abziehen)
Minuend - Subtrahend = Differenz 4 - 1 = 3
Multiplizieren
(Malnehmen) Multiplikand · Multiplikator = Produkt
Faktor · Faktor = Produkt 4 · 2 = 8
Dividieren
(Teilen)
Dividend : Divisor = Quotient 8 : 2 = 4
Die Division ist nur für Divisoren ≠ 0 definiert.
Regeln
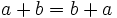 Kommutativgesetz der Addition
Kommutativgesetz der Addition
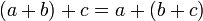 Assoziativgesetz der Addition
Assoziativgesetz der Addition
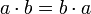 Kommutativgesetz der Multiplikation
Kommutativgesetz der Multiplikation
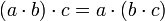 Assoziativgesetz der Multiplikation
Assoziativgesetz der Multiplikation
Bruchrechnen
Echter Bruch
Der Zähler ist kleiner als der Nenner und es gibt kein Ganzes. (Der Wert ist immer kleiner als 1).
Unechter Bruch
Der Zähler ist größer als der Nenner und es gibt dann mindestens ein Ganzes.
Dezimalbruch
Gemischte Zahl
Ganze Zahl und ein Bruch.
Gleichnamige Brüche
Alle Nenner sind gleich.
Ungleichnamige Brüche
Nicht alle Nenner sind gleich.
Kürzen von Brüchen
Zähler und Nenner werden durch die gleiche Zahl (hier 2) dividiert. Man kann maximal durch den größten gemeinsamen Teiler des Nenners und des Zählers dividieren. Der Wert des Bruches bleibt dabei erhalten.
Erweitern von Brüchen
Zähler und Nenner werden mit der gleichen Zahl ≠ 0 (hier 3) multipliziert, dabei bleibt der Wert des Bruches erhalten.
Addieren und Subtrahieren gleichnamiger Brüche
Die Zähler werden addiert oder subtrahiert und der Nenner wird beibehalten.
Addieren und Subtrahieren ungleichnamiger Brüche
Beispiel 1:
Beispiel 2:
Die Nenner werden durch Erweitern auf ein gemeinsames Vielfaches, meist das kleinste gemeinsame Vielfache (kgV) aller Nenner, gebracht und somit zu gleichnamigen Brüchen. Ermittlung des kgV beispielsweise mit Hilfe der Primfaktorzerlegung
Multiplizieren von Brüchen
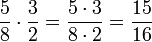
Zähler mal Zähler durch Nenner mal Nenner.
Dividieren von Brüchen
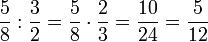 (gekürzt)
(gekürzt)Den Dividend mal dem Kehrwert des Divisors. (Man vertauscht einfach beim zweiten Bruch Nenner und Zähler.)
Umwandeln von Dezimalbrüchen
Abbrechende Dezimalbrüche werden als Bruch mit einer Zehnerpotenz im Nenner geschrieben und anschließend gekürzt:
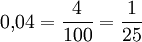
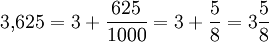
Bei periodischen Dezimalbrüchen vermindert man die Zehnerpotenz um 1 (Zahl mit so viel Neunen, wie die Periodenlänge angibt):
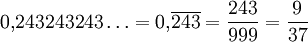
Nicht sofort periodischer Fall:
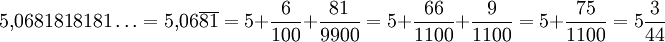
Dezimalzahlen, die weder abbrechen noch periodisch werden, lassen sich nicht exakt als Bruch
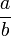 schreiben.
schreiben.
Wikimedia Foundation.