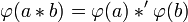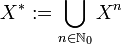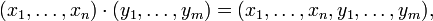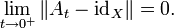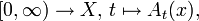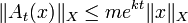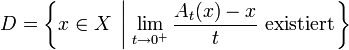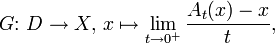- Unterhalbgruppe
-
Halbgruppe (Axiome EA) berührt die Spezialgebiete
ist Spezialfall von
- Magma (Axiom E)
umfasst als Spezialfälle
- Monoid (EAN)
- Gruppe (EANI)
- Abelsche Gruppe (EANIK)
- Gruppe (EANI)
- kommutative Halbgruppe (EAK)
- natürliche Zahlen (N+,+)
- kommutatives Monoid (EANK)
- natürliche Zahlen (N,+)
In der Mathematik ist eine Halbgruppe eine algebraische Struktur bestehend aus einer nichtleeren Menge mit einer inneren zweistelligen Verknüpfung, die dem Assoziativgesetz genügt (also ein assoziatives Magma). Auf die Anforderung der Nichtleerheit kann auch verzichtet werden, dann ist die leere Menge trivialerweise eine (dann die kleinste) Halbgruppe.
Inhaltsverzeichnis
Definitionen
Halbgruppe
Eine Halbgruppe
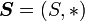 besteht aus einer nichtleeren Menge S und einer inneren zweistelligen Verknüpfung
besteht aus einer nichtleeren Menge S und einer inneren zweistelligen Verknüpfungdie assoziativ ist, d. h. für alle
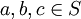 gilt
gilt- a * (b * c) = (a * b) * c.
Man muss nicht voraussetzen, dass S nichtleer ist. Die leere Menge
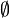 bildet dann auch eine Halbgruppe bezüglich der leeren Verknüpfung
bildet dann auch eine Halbgruppe bezüglich der leeren Verknüpfung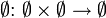 ,
,
die leere oder triviale Halbgruppe
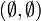 genannt wird.
genannt wird.Bemerkungen zur Notation
Häufig wird für die Verknüpfung * das Symbol
 benutzt, man spricht dann von einer multiplikativ geschriebenen Halbgruppe. Wie auch bei der gewöhnlichen Multiplikation üblich, kann in vielen Situationen der Malpunkt
benutzt, man spricht dann von einer multiplikativ geschriebenen Halbgruppe. Wie auch bei der gewöhnlichen Multiplikation üblich, kann in vielen Situationen der Malpunkt  weggelassen werden.
weggelassen werden.Eine Halbgruppe lässt sich auch additiv notieren, indem für die Verknüpfung * das Symbol + benutzt wird.
Mit der Gültigkeit des Assoziativgesetzes lässt sich eine vereinfachte klammerfreie Notation einführen, denn sei
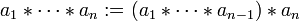 für jedes
für jedes 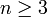 ,
,
dann haben alle Verknüpfungen von
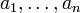 , die sich nur in der Klammerung von
, die sich nur in der Klammerung von 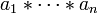 unterscheiden, das gleiche Ergebnis wie
unterscheiden, das gleiche Ergebnis wie 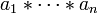 (allgemeines Assoziativgesetz, Beweis: vollständige Induktion über n), man kann also für jede dieser Verknüpfungen einfach nur
(allgemeines Assoziativgesetz, Beweis: vollständige Induktion über n), man kann also für jede dieser Verknüpfungen einfach nur 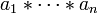 schreiben.[1]
schreiben.[1]Unterhalbgruppe
Seien
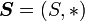 eine Halbgruppe und
eine Halbgruppe und 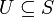 . Ist dann
. Ist dann 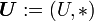 eine Halbgruppe ( * ist hier eine vereinfachte Schreibweise für die Einschränkung
eine Halbgruppe ( * ist hier eine vereinfachte Schreibweise für die Einschränkung 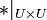 von * auf
von * auf 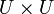 ), so heißt
), so heißt 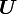 Unterhalbgruppe von
Unterhalbgruppe von 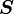 .
. 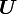 ist genau dann eine Unterhalbgruppe von
ist genau dann eine Unterhalbgruppe von 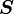 , wenn U abgeschlossen ist bezüglich * , d. h. es gilt
, wenn U abgeschlossen ist bezüglich * , d. h. es gilt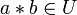 für alle
für alle 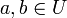 .
.
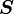 nennt man dann auch Oberhalbgruppe von
nennt man dann auch Oberhalbgruppe von 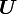 .
.Faktorhalbgruppe
Ist
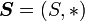 eine Halbgruppe und
eine Halbgruppe und 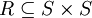 eine mit * verträgliche Äquivalenzrelation auf S, so bildet die Faktormenge S / R von S nach R zusammen mit der durch
eine mit * verträgliche Äquivalenzrelation auf S, so bildet die Faktormenge S / R von S nach R zusammen mit der durchdefinierten Verknüpfung
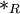 ebenfalls eine Halbgruppe. Diese Halbgruppe
ebenfalls eine Halbgruppe. Diese Halbgruppe 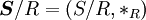 heißt die Faktorhalbgruppe oder Quotientenhalbgruppe von
heißt die Faktorhalbgruppe oder Quotientenhalbgruppe von 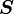 nach R. Die Verknüpfung
nach R. Die Verknüpfung 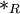 wird die durch die Äquivalenzrelation induzierte Verknüpfung oder die kanonische Verknüpfung der Faktorhalbgruppe genannt.
wird die durch die Äquivalenzrelation induzierte Verknüpfung oder die kanonische Verknüpfung der Faktorhalbgruppe genannt.Halbgruppenhomomorphismus
Eine Abbildung
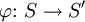 zwischen zwei Halbgruppen
zwischen zwei Halbgruppen 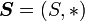 und
und 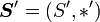 heißt Halbgruppenhomomorphismus, wenn gilt:
heißt Halbgruppenhomomorphismus, wenn gilt:für alle
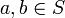 . Ist aus dem Zusammenhang klar, das es sich um einen Homomorphismus zwischen Halbgruppen handelt, so lässt man den Zusatz Halbgruppen- auch weg. Je nachdem, ob
. Ist aus dem Zusammenhang klar, das es sich um einen Homomorphismus zwischen Halbgruppen handelt, so lässt man den Zusatz Halbgruppen- auch weg. Je nachdem, ob  injektiv oder surjektiv oder beides ist, heißt der Homomorphismus
injektiv oder surjektiv oder beides ist, heißt der Homomorphismus  Mono-, Epi- bzw. Isomorphismus. Gilt S = T so heißt der Homomorphismus Endomorphismus von H und der Isomorphismus Automorphismus von H.
Mono-, Epi- bzw. Isomorphismus. Gilt S = T so heißt der Homomorphismus Endomorphismus von H und der Isomorphismus Automorphismus von H.Eigenschaften
Es folgt eine Übersicht über grundlegende algebraische Eigenschaften, interpretiert und angewandt auf Halbgruppen. Genauere Informationen finden sich in den entsprechenden Hauptartikeln.
Kommutativität
Die Halbgruppe
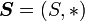 heißt kommutativ oder auch abelsch, wenn
heißt kommutativ oder auch abelsch, wenn- b * a = a * b
für alle
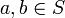 gilt. Die Verknüpfung * selbst wird hierbei auch als kommutativ bezeichnet.
gilt. Die Verknüpfung * selbst wird hierbei auch als kommutativ bezeichnet.Idempotenz
Ein Element
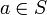 einer Halbgruppe
einer Halbgruppe 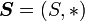 heißt idempotent, wenn
heißt idempotent, wenn- a * a = a
gilt. Man nennt
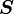 idempotent, wenn jedes
idempotent, wenn jedes 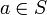 diese Eigenschaft hat.
diese Eigenschaft hat.Neutrales Element
Ein Element
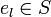 (bzw.
(bzw. 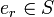 ) einer Halbgruppe
) einer Halbgruppe 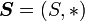 heißt linksneutral (bzw. rechtsneutral), wenn für alle
heißt linksneutral (bzw. rechtsneutral), wenn für alle 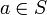 gilt:
gilt:- el * a = a (bzw. a * er = a).
Ist
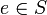 sowohl links- als auch rechtsneutral, so heißt es neutral. Gibt es in einer Halbgruppe sowohl ein links- als auch ein rechtsneutrales Element, so sind diese identisch und somit neutral. In einer Halbgruppe gibt es höchstens ein neutrales Element (ansonsten nur links- oder nur rechtsneutrale oder weder noch), man spricht dann von dem neutralen Element von
sowohl links- als auch rechtsneutral, so heißt es neutral. Gibt es in einer Halbgruppe sowohl ein links- als auch ein rechtsneutrales Element, so sind diese identisch und somit neutral. In einer Halbgruppe gibt es höchstens ein neutrales Element (ansonsten nur links- oder nur rechtsneutrale oder weder noch), man spricht dann von dem neutralen Element von 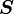 . Eine Halbgruppe mit neutralem Element nennt man auch Monoid.
. Eine Halbgruppe mit neutralem Element nennt man auch Monoid.Hinweis: In den folgenden Definitionen wird nur die linksseitige Variante stellvertretend für die entsprechende rechts- und beidseitige Variante aufgeführt; die rechts- und beidseitigen Varianten sind in der Mathematik analog definiert. Absorption
Ein Element
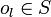 heißt linksabsorbierend in (S, * ), wenn für alle
heißt linksabsorbierend in (S, * ), wenn für alle 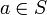 gilt:
gilt:- ol * a = ol.
Es gibt höchstens ein absorbierendes (d. h. links- und rechtsabsorbierendes) Element in einer Halbgruppe.
Kürzbarkeit
Ein Element
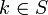 heißt linkskürzbar oder auch linksregulär in
heißt linkskürzbar oder auch linksregulär in 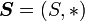 , wenn für alle
, wenn für alle 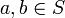 gilt:
gilt: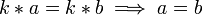 .
.
Ist jedes Element aus S linkskürzbar, so heißt
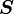 linkskürzbar oder linksregulär. Eine endliche, kürzbare (d. h. links- und rechtskürzbare) Halbgruppe ist eine Gruppe.
linkskürzbar oder linksregulär. Eine endliche, kürzbare (d. h. links- und rechtskürzbare) Halbgruppe ist eine Gruppe.Invertierbarkeit und Inverses
Mit neutralem Element
Besitzt
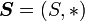 ein linksneutrales Element
ein linksneutrales Element 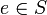 , so heißt ein Element
, so heißt ein Element 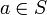 linksinvertierbar in
linksinvertierbar in 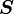 , wenn ein
, wenn ein 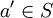 existiert mit
existiert mit- a' * a = e.
In diesem Falle nennt man a' ein Linksinverses von a.
Ist jedes Element aus S linksinvertierbar, so ist auch jedes Element rechtsinvertierbar und alle Inversen eines Elements stimmen überein,
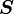 ist dann eine Gruppe.
ist dann eine Gruppe.Ohne Neutrales Element
Besitzt
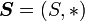 kein linksneutrales Element, so heißt ein Element
kein linksneutrales Element, so heißt ein Element 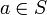 linksinvertierbar in
linksinvertierbar in 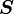 , wenn für alle
, wenn für alle 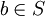 ein
ein 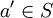 existiert mit
existiert mit- a' * (a * b) = b.
In diesem Falle nennt man a' ein Linksinverses von a.
Ist jedes Element aus S in diesem Sinne invertierbar (d. h. links- und rechtsinvertierbar), so folgt die eindeutige Existenz eines neutralen Elements und
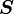 ist eine Gruppe.
ist eine Gruppe.Beispiele
Zur Entstehung des Namens
Die Menge
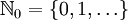 der natürlichen Zahlen bildet mit der gewöhnlichen Addition eine kommutative und kürzbare Halbgruppe
der natürlichen Zahlen bildet mit der gewöhnlichen Addition eine kommutative und kürzbare Halbgruppe 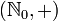 , die keine Gruppe ist. Da hier die negativen Zahlen fehlen, also die Hälfte der abelschen Gruppe
, die keine Gruppe ist. Da hier die negativen Zahlen fehlen, also die Hälfte der abelschen Gruppe 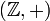 der ganzen Zahlen, lag der Name Halbgruppe für diese Struktur nahe. Tatsächlich wurde in der Vergangenheit der Begriff „Halbgruppe“ für ein nach den oben gegebenen Definitionen kommutatives, kürzbares Monoid verwendet,[2] später setzte sich dann die obige Definition allgemein durch.
der ganzen Zahlen, lag der Name Halbgruppe für diese Struktur nahe. Tatsächlich wurde in der Vergangenheit der Begriff „Halbgruppe“ für ein nach den oben gegebenen Definitionen kommutatives, kürzbares Monoid verwendet,[2] später setzte sich dann die obige Definition allgemein durch.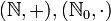 und
und 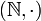 bilden Beispiele für kommutative Halbgruppen mit verschiedenen Eigenschaften bezüglich neutraler und absorbierender Elemente sowie der Kürzbarkeit.
bilden Beispiele für kommutative Halbgruppen mit verschiedenen Eigenschaften bezüglich neutraler und absorbierender Elemente sowie der Kürzbarkeit.Transformationshalbgruppen
Für eine beliebige Menge X sei
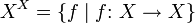 die Menge aller Abbildungen (Transformationen) von X in sich. Bezeichnet
die Menge aller Abbildungen (Transformationen) von X in sich. Bezeichnet  die Nacheinanderanwendung von Abbildungen
die Nacheinanderanwendung von Abbildungen 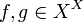 , also
, also 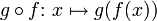 , dann ist
, dann ist 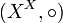 eine Halbgruppe, die volle Transformationshalbgruppe oder symmetrische Halbgruppe auf X. Idempotente Elemente in XX sind z.B. für jedes
eine Halbgruppe, die volle Transformationshalbgruppe oder symmetrische Halbgruppe auf X. Idempotente Elemente in XX sind z.B. für jedes 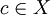 die konstanten Abbildungen
die konstanten Abbildungen 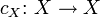 mit cX(x) = c für alle
mit cX(x) = c für alle  , aber auch die identische Abbildung
, aber auch die identische Abbildung 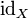 auf X als neutrales Element. Unterhalbgruppen von
auf X als neutrales Element. Unterhalbgruppen von 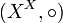 heißen Transformationshalbgruppen auf X.[3]
heißen Transformationshalbgruppen auf X.[3]Anwendung
Formale Sprachen
Für eine beliebige Menge
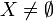 sei
seidie kleenesche Hülle von X. Definiert man für alle
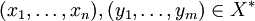 eine Multiplikation durch
eine Multiplikation durchdann ist
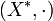 eine Halbgruppe, die freie Halbgruppe über X. Schreibt man die Elemente
eine Halbgruppe, die freie Halbgruppe über X. Schreibt man die Elemente 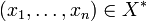 einfach in der Form
einfach in der Form 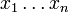 , dann heißen die Elemente in X * Worte über dem Alphabet X,
, dann heißen die Elemente in X * Worte über dem Alphabet X, 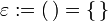 ist das leere Wort und die Multiplikation
ist das leere Wort und die Multiplikation  bezeichnet man als Konkatenation.[4] In der theoretischen Informatik setzt man in der Regel voraus, dass ein Alphabet endlich ist, Teilmengen der kleeneschen Hülle eines Alphabets mit dem leeren Wort nennt man formale Sprachen.[5]
bezeichnet man als Konkatenation.[4] In der theoretischen Informatik setzt man in der Regel voraus, dass ein Alphabet endlich ist, Teilmengen der kleeneschen Hülle eines Alphabets mit dem leeren Wort nennt man formale Sprachen.[5]Funktionalanalysis, Partielle Differentialgleichungen
Halbgruppen spielen auch eine Rolle in der Lösungstheorie partieller Differentialgleichungen. Sei
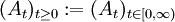 eine Familie beschränkter Transformationen
eine Familie beschränkter Transformationen 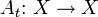 auf einem vollständigen metrischen Raum (X,d), d.h. zu jedem
auf einem vollständigen metrischen Raum (X,d), d.h. zu jedem 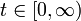 existiert ein
existiert ein 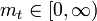 mit
mit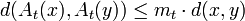 für alle
für alle 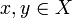 .
.
Insbesondere ist dann jedes At stetig und
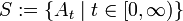 bildet eine kommutative Halbgruppe
bildet eine kommutative Halbgruppe 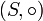 mit neutralem Element
mit neutralem Element 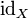 , wenn gilt:
, wenn gilt: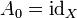 und
und
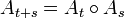 für alle
für alle 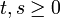 .
.
Die Funktion
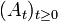 ist ein Halbgruppenhomomorphismus von
ist ein Halbgruppenhomomorphismus von 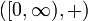 nach
nach 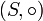 und wird eine einparametrige Halbgruppe von Operatoren genannt (siehe auch: kontinuierliches dynamisches System). Ein At ist außerdem kontraktiv, falls
und wird eine einparametrige Halbgruppe von Operatoren genannt (siehe auch: kontinuierliches dynamisches System). Ein At ist außerdem kontraktiv, falls- d(At(x),At(y)) < d(x,y) ist für alle
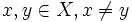 .[6]
.[6]
Sind alle At beschränkte lineare Operatoren auf einem Banachraum
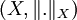 , dann heißt
, dann heißt 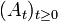 gleichmäßig stetig, wenn für die Operatornorm gilt:
gleichmäßig stetig, wenn für die Operatornorm gilt:Falls die Abbildungen
stetig sind für alle
 , wird die Halbgruppe stark stetig genannt. Ist
, wird die Halbgruppe stark stetig genannt. Ist 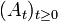 eine stark stetige Halbgruppe, so existieren feste
eine stark stetige Halbgruppe, so existieren feste 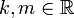 mit
mit 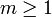 , so dass
, so dassgilt. Kann k = 0 gewählt werden, nennt man
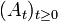 eine beschränkte einparametrige Halbgruppe.
eine beschränkte einparametrige Halbgruppe.Der auf der Teilmenge
von X definierte lineare Operator
heißt infinitesimaler Generator oder Erzeuger der Halbgruppe
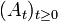 .
.Einzelnachweise
- ↑ Mario Petrich: Introduction to Semigroups. S. 4. P.A. Grillet: Semigroups: An Introduction to the Structure Theory. S. 4f.
- ↑ vgl. P. Lorenzen: Abstrakte Begründung der multiplikativen Idealtheorie. Math. Z. 45 (1939), 533–553.
- ↑ J.M. Howie: Fundamentals of Semigroup Theory. S. 6. P.A. Grillet: Semigroups: An Introduction to the Structure Theory. S. 2.
- ↑ U. Hebisch, H.J. Weinert: Halbringe: Algebraische Theorie und Anwendungen in der Informatik. S. 244.
- ↑ John E. Hopcroft, Jeffrey D. Ullman: Einführung in die Automatentheorie, formale Sprachen und Komplexitätstheorie. 2. Aufl., Addison-Wesley (Deutschland), Bonn, München u.a. 1990, ISBN 3-89319-181-x. S. 1.
- ↑ E. Hille: Methods in Classical and Functional Analysis. Addison-Wesley, Reading (Mass.) u.a. 1972. S. 165ff.
Literatur
- Pierre Antoine Grillet: Semigroups: An Introduction to the Structure Theory. Marcel Dekker, New York 1995, ISBN 0-8247-9662-4.
- Udo Hebisch, Hanns Joachim Weinert: Halbringe: Algebraische Theorie und Anwendungen in der Informatik. B.G. Teubner, Stuttgart 1993, ISBN 3-519-02091-2.
- John F. Berglund, Hugo D. Junghenn, Paul Milnes: Analysis on Semigroups: Function Spaces, Compactifications, Representations. John Wiley & Sons, New York et al. 1989, ISBN 0-471-61208-1.
- John M. Howie: Fundamentals of Semigroup Theory. Oxford University Press, Oxford 1995, ISBN 0-19-851194-9.
- Mario Petrich: Introduction to Semigroups. Bell & Howell, Columbus, Ohio, 1973, ISBN 0-675-09062-8.
Siehe auch
Wikimedia Foundation.

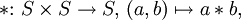
![[a] {\;*}_{R\;} [b] := [a*b]](/pictures/dewiki/53/5d38a43b8a7210a55650274026caea67.png)