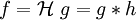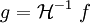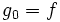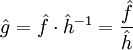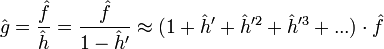- Van Cittert Dekonvolution
-
Die Van Cittert deconvolution ist ein Verfahren, um die Faltung eines Bildes g mit einer Filtermaske (PSF) h rückgängig zu machen (Dekonvolution/inverse Filterung). Sie kann damit zur Verbesserung der Bildqualität benutzt werden, wenn das Bild z.B. durch ein unscharfes Objektiv oä. "verwaschen" wurde. Das Bild g stellt das ideale Bild dar, das man gerne als Ergebnis des Verfahrens erhalten möchte. Das verwaschene Bild f, das den Ausgangspunkt des Verfahrens darstellt ist:
Dabei bedeutet
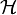 den Filteroperator, der durch Faltung mit h dargestellt wird. Man möchte gerne folgenden Ausdruck berechnen:
den Filteroperator, der durch Faltung mit h dargestellt wird. Man möchte gerne folgenden Ausdruck berechnen:Die Van Cittert Deconvolution besteht aus folgender iterativer Formel:
Dabei ist
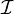 ein Operator, dessen Punktantwort I einem Delta-Puls entspricht (überall 0, nur in der Mitte 1). Die Operation
ein Operator, dessen Punktantwort I einem Delta-Puls entspricht (überall 0, nur in der Mitte 1). Die Operation 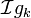 ergibt also gerade gk. Die Stärke der Rückfaltung hängt von der Anzahl der Iterationsschritte k ab. Je mehr Iterationsschritte durchgeführt werden, desto stärker ist die Rückfaltung (Schärfung). Dafür wird das Bildrauschen bei zu großer Anzahl an Iterationen verstärkt und das Bild wird wieder undeutlich.
ergibt also gerade gk. Die Stärke der Rückfaltung hängt von der Anzahl der Iterationsschritte k ab. Je mehr Iterationsschritte durchgeführt werden, desto stärker ist die Rückfaltung (Schärfung). Dafür wird das Bildrauschen bei zu großer Anzahl an Iterationen verstärkt und das Bild wird wieder undeutlich.Beispiel
Die folgenden Bilder zeigen die Anwendung der Van Cittert Iteration auf ein weichgezeichnetes Bild (3x3-Gauß-Filter):

Herleitung
Im Fourierraum wird die Faltung zu einer punktweise Multiplikation, sodass gilt:
Dies lässt sich leicht berechnen, wenn die Transferfunktion
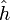 keine Nullstellen enthält, da sonst eine Division durch 0 nötig wäre. Um dieses Problem zu umgehen führt man
keine Nullstellen enthält, da sonst eine Division durch 0 nötig wäre. Um dieses Problem zu umgehen führt man 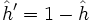 ein. Damit gilt dann:
ein. Damit gilt dann:Im letzten Schritt wurde eine Taylor-Entwicklung durchgeführt. Im Ortsraum ergibt dieser Ausdruck:
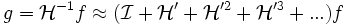 mit
mit 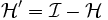 .
.
Unter Ausnutzung des Horner-Schemas für dieses Polynom erhält man obige Iterationsvorschrift:
- g0 = f
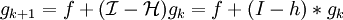
Literatur
- Bernd Jähne: Digitale Bildverarbeitung. Springer Verlag, Mai 2005 6.Auflage ISBN 3540249990
Wikimedia Foundation.