Van Deemter Gleichung

Die van-Deemter-Gleichung (JJ van Deemter, 1956) beschreibt mathematisch/physikalisch die Trennleistung in der Gas- und Flüssig-Chromatographie.
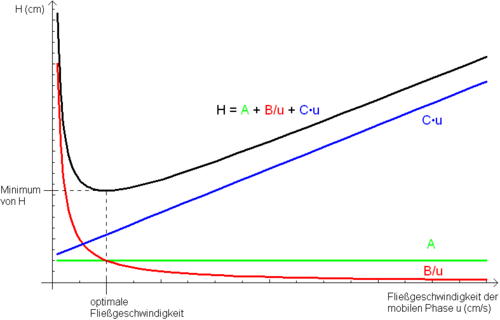
Die Bodenhöhe H (HETP - Höhenäquivalent eines theoretischen Bodens, engl. height equivalent to a theoretical plate) wird durch folgende vereinfachte Formel beschrieben: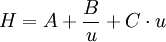

$H = A + \frac{B}{u} + C \cdot u$

Van-Deemter Plot

Je kleiner H ist, desto größer ist die Trennleistung des Systems. Dies folgt aus der Gleichung:

$H = \frac{L}{N}$

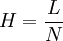
Die H/v-Hyperbelfunktion (X = u, Y = HETP) hat ein Minimum bei der optimalen Strömungsgeschwindigkeit (u), bei der die Bodenhöhe (H) am geringsten und damit die Trennleistung am größten ist.

• H - Bodenhöhe
• L - Länge der Säule
• N - Trennstufenzahl
• u - Geschwindigkeit der mobilen Phase
• A - Streudiffusion/Wirbeldiffusion (Eddy-Diffusion). Bei gepackten Säulen erhöht die Verwirbelung diesen Term. Er ist unabhängig von der Strömungsgeschwindigkeit. Bei Kapillarsäulen entfällt A.
• B - Longitudinal-Diffusion, Diffusion in Längsrichtung. Dieser Faktor ist abhängig von der Viskosität und Temperatur der mobilen Phase. Er ist abhängig vom Kehrwert der Strömungsgeschwindigkeit.
• C - beschreibt den Massenübergang zwischen stationärer und mobiler Phase. Dieser Term wird durch die Art der mobilen Phase und die Art und Dicke der stationären Phase beeinflusst. Er ist direkt proportional zur Strömungsgeschwindigkeit.

Term A ist außerdem vom Teilchendurchmesser der stationären Phase abhängig: A = 2 λ d (λ = Faktor, d = Teilchendurchmesser).

Term B ist von dem Diffusionskoeffizient der mobilen Phase (D(M)) abhängig: B = 2 λ D(M).

Term C ist auch vom Teilchendurchmesser, der Porösität der Teilchen, der Säulenlänge, dem Säulenradius sowie dem Diffusionskoeffizienten der stationären Phase abhängig.

Literatur

• Van Deemter, et. al.: Chem. Eng. Sci., 5 (1956) 271