Vektoruhr

Eine Vektoruhr ist eine Softwarekomponente (oder ein Protokoll) zum Zuweisen von eindeutigen Zeitstempeln an Nachrichten. Sie ist also eine logische Uhr, die es erlaubt, den Ereignissen in einem Verteilten System aufgrund eines Zeitstempels eine Kausalordnung zuzuweisen (Sequentialisierung) und insbesondere die Nebenläufigkeit von Ereignissen zu ermitteln. Sie stellt eine Erweiterung der Lamport-Uhr dar, die auch der starken Uhrenbedingung genügt. Vektoruhren wurden von mehreren Wissenschaftlern unabhängig voneinander entwickelt, insbesondere von Colin J. Fidge, Friedemann Mattern und Frank Bernhard Schmuck.

Beispiel eines Systems von Vektoruhren

Funktionsweise

Das Vorgehen beim Betrieb von Vektoruhren ist wie folgt: Ähnlich wie bei der Lamport-Uhr führt jeder Prozess einen Zähler, der bei jedem Ereignis (insbesondere beim Senden und Empfangen von Nachrichten) erhöht wird. Aber anders als bei der Lamport-Uhr besteht hier die Uhr jedes Prozesses nicht nur aus einem Zähler, sondern aus einem Vektor (bzw. einem Array oder einer assoziativen Liste) von Zählern: Jeder Prozess merkt sich den Zählerstand aller anderen Prozesse, soweit der bekannt ist. Der aktuelle Stand der Uhr wird jeder gesendeten Nachricht angehängt.

Bei jedem Ereignis wird immer nur der eigene Zähler erhöht. Wird eine Nachricht empfangen, wird aus dem aktuellen und dem empfangenen Vektor ein elementweises Maximum gebildet, um den neuen Stand der Uhr zu ermitteln.

Als Pseudocode sieht die Umsetzung einer Vektoruhr so aus: Routine zum Senden einer Nachricht:

Uhr[PID]= Uhr[PID]+1;
Zeitstempel= Uhr;
sende(Nachricht,Zeitstempel);

Dabei sei PID für jeden Prozess ein fest vorgegebener und eindeutiger Bezeichner, zum Beispiel eine Prozess-ID oder eine IP-Adresse (oder auch eine Kombination aus diesen beiden). Die Felder der Uhr für die Prozesse, von denen noch keine Nachricht empfangen wurde, werden als null angenommen.

Routine zum Empfangen einer Nachricht:

(Nachricht,Zeitstempel)= empfange();
Uhr[PID]= Uhr[PID]+1;
 
for (Prozesse P) do begin
    Uhr[P]= max(Uhr[P],Zeitstempel[P]);
end;

Partielle Ordnung

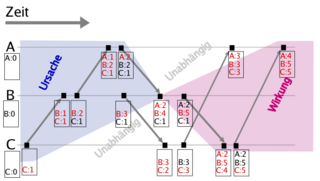
Um nun anhand der Zeitstempel entscheiden zu können, welche Nachricht (bzw. welches Ereignis) von welcher anderen kausal abhängig ist, wird über den Ständen der Vektoruhr eine partielle Ordnungsrelation definiert: ein Ereignis A ist eine Ursache von Ereignis B, wenn der Zähler für jeden Prozess im Zeitstempel C(A) kleiner oder gleich dem Zähler im Zeitstempel C(B) für den korrespondierenden Prozess und für mindestens einen dieser Zähler strikt kleiner ist. In Zeichen:

C(A) = (A₁,A₂,A₃...A_n)

$A \rightarrow B \Leftrightarrow \forall_{1\le i\le n}: A_i \le B_i \and \exists i': A_{i'} < B_{i'}$

Da für Vektoruhren die Implikation in beide Richtungen gültig ist, erfüllen sie die starke Uhrenbedingung.

Eine Umsetzung der obigen Ordnungsrelation in Pseudocode (A und B seien die zu vergleichenden Zeitstempel, die Frage ist, ob A eine Ursache von B war):

procedure ist_ursache(A,B):
    mindestens_ein_element_strikt_kleiner = NEIN;
    for (Prozesse P) do begin
        if ( A[P] > B[P] ) then return NEIN;
        if ( A[P] < B[P] ) then mindestens_ein_element_strikt_kleiner := JA;
    end;
     
    return mindestens_ein_element_strikt_kleiner;
end procedure;

Nebenläufigkeit

Es ist durchaus möglich, dass weder A → B noch B → A gilt, die genannte Prozedur somit bei den Aufrufen

ist_ursache(A,B)
ist_ursache(B,A)

jeweils NEIN als Antwort zurückliefert: Die Ereignisse sind dann nebenläufig, man schreibt auch A || B. Es ist gerade der entscheidende Vorteil von Vektoruhren über den einfacheren Lamport-Uhren, dass es aufgrund der Zeitstempel möglich ist, zu erkennen, welche Ereignisse nebenläufig sind. Das ergibt sich aus der Gültigkeit der starken Uhrenbedingung. Zu beachten ist hierbei, dass im Gegensatz zur Ursachenrelation die Nebenläufigkeit nicht transitiv ist.

Literatur

• C. J. Fidge, Timestamps in message-passing systems that preserve the partial ordering, In K. Raymond, editor, Proc. of the 11th Australian Computer Science Conference (ACSC'88), pp. 56–66, February 1988. [1]
• Reinhard Schwarz und Friedemann Mattern, Detecting Causal Relationships in Distributed Computations: In Search of the Holy Grail, in Distributed Computing, Nr. 3 Vol. 7, Springer 1994. [2]