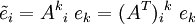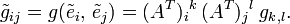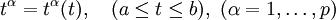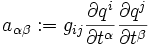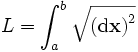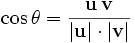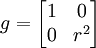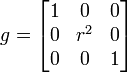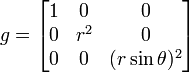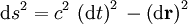- Vergleich von Tensordefinitionen
-
Der metrische Tensor (auch Metriktensor oder Maßtensor) dient dazu, mathematische Räume, insbesondere differenzierbare Mannigfaltigkeiten, mit einem Maß für Abstände und Winkel auszustatten.
Dieses Maß muss nicht notwendig alle Bedingungen erfüllen, die in der Definition eines metrischen Raums an eine Metrik gestellt werden: im Minkowski-Raum der Speziellen Relativitätstheorie gelten diese Bedingungen nur für Abstände, die entweder einheitlich raumartig oder einheitlich zeitartig sind.
Für die Differentialgeometrie und die Allgemeine Relativitätstheorie bedeutsam ist, dass der metrische Tensor, anders als eine über inneres Produkt und Norm definierte Metrik, vom Ort abhängen kann.
Inhaltsverzeichnis
Definition und Bedeutung
Der metrische Tensor g über einem affinen Punktraum A mit reellem Verschiebungsvektorraum V ist eine Abbildung von A in den Raum der Skalarprodukte auf V. D.h. für jeden Punkt
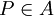 ist
isteine positiv definite, symmetrische Bilinearform .
In Anlehnung an die Unterscheidung zwischen Metrik und Pseudometrik wird manchmal auch der Fall betrachtet, dass g(P) für einige oder alle Punkte P nur positiv semidefinit ist, d.h. die Forderung der Definitheit
-
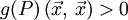 für alle
für alle 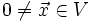
wird abgeschwächt zu
-
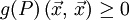 für alle
für alle 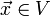 .
.
Eine solcher Tensor g heißt dann pseudometrischer Tensor.
Ein metrischer Tensor definiert eine (vom Punkt P abhängige) Länge
auf dem Vektorraum V. Analog zum euklidischen Skalarprodukt ist der Winkel
![\theta\in[0,\pi]=[0^o, 180^o]](/pictures/dewiki/49/145775be241442085081afdbbfa70cc1.png) im Punkt P zwischen zwei Vektoren
im Punkt P zwischen zwei Vektoren 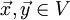 durch
durchdefiniert.
Länge von Kurven
Ist eine differenzierbare Kurve
![\gamma:[a,b]\to A](/pictures/dewiki/54/6b5de189e0ca5742d8a9b7ff486cd633.png) im affinen Punktraum gegeben, so hat diese in jedem Zeitpunkt t einen Tangentialvektor
im affinen Punktraum gegeben, so hat diese in jedem Zeitpunkt t einen Tangentialvektor-
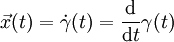 .
.
Der gesamten Kurve oder einem Segment davon kann man nun mit Hilfe des metrischen Tensors eine Länge
zuordnen.
Koordinatendarstellung
Wenn ein lokales Koordinatensystem (xi) auf V mit Basis (ei) aus V gewählt wird, schreibt man die Komponenten von g als gij(P) = g(P)(ei,ej). Unter Verwendung der Einsteinschen Summationskonvention ist dann für die Vektoren
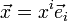 und
und 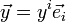
-
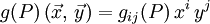 .
.
Im Sinne der Kategorientheorie ist der metrische Tensor kontravariant, da unter (affin) linearen injektiven Abbildungen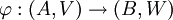 natürlicherweise aus einem metrischen Tensor auf (B,W) ein metrischer Tensor auf (A,V) konstruiert werden kann,
natürlicherweise aus einem metrischen Tensor auf (B,W) ein metrischer Tensor auf (A,V) konstruiert werden kann,-
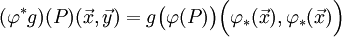 .
.
In der Physik wird der metrische Tensor, oder besser seine Koordinatendarstellung gij als kovariant bezeichnet, da sich seine Komponenten unter einem Koordinatenwechsel in jedem Index wie die Basis transformieren. Ist ein Koordinatenwechsel als
-
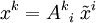 bzw.
bzw. 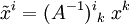
gegeben, so transformieren sich Basisvektoren als
und es gilt für den metrischen Tensor
Induzierter Metriktensor
Hat man eine p-dimensionale Untermannigfaltigkeit eines Riemannschen Raumes mit der Metrik (gij), die mittels der Parameterdarstellung qi = qi(t1,t2,...,tp) (
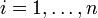 ) gegeben ist (ti,
) gegeben ist (ti, 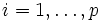 nennt man auch induzierte Koordinaten), und betrachtet man eine Kurve
nennt man auch induzierte Koordinaten), und betrachtet man eine Kurveauf dieser Teilmannigfaltigkeit, so erhält man für die Bogenlänge gemäß der Kettenregel
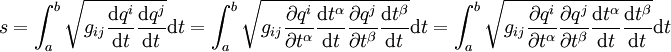 .
.
Die Größe
nennt man induzierten Metriktensor. Mit diesem ergibt sich die Kurvenlänge schließlich als
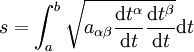 .
.
Beispiele
Euklidischer Raum
In einem Euklidischen Raum mit Kartesischen Koordinaten ist der metrische Tensor durch die Einheitsmatrix gegeben,
- gij = δij.
Für die Kurvenlänge
und den Winkel
erhält man die üblichen Formeln der Vektoranalysis.
Wenn eine Mannigfaltigkeit in einen Euklidischen Raum mit kartesischen Koordinaten eingebettet ist, dann ergibt sich ihr metrischer Tensor aus der Jacobi-Matrix J der Einbettung als
- g = JTJ.
In einigen anderen Koordinatensystemen lautet der metrische Tensor des Euklidischen Raums wie folgt:
- In Polarkoordinaten (x1,x2) = (r,θ):
- In Zylinderkoordinaten (x1,x2,x3) = (r,θ,z):
- In Kugelkoordinaten
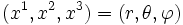 :
:
Minkowski-Raum (spezielle Relativitätstheorie)
Hauptartikel: Minkowski-Raum
Der flache Minkowski-Raum der speziellen Relativitätstheorie beschreibt eine vierdimensionale Raum-Zeit ohne Gravitation. Räumliche Abstände und Zeitspannen hängen in diesem Raum von der Wahl eines Inertialsystems ab; wenn man einen physikalischen Vorgang in zwei verschiedenen, gleichförmig gegeneinander bewegten Inertialsystemen beschreibt, können sie verschiedene Werte annehmen.
Invariant unter Lorentztransformationen ist hingegen der sogenannte Viererabstand, der räumliche und zeitliche Abstände zusammenfasst. Unter Verwendung der Lichtgeschwindigkeit c berechnet sich dieser Viererabstand aus räumlichem Abstand
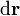 und Zeitspanne
und Zeitspanne 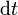 als
alsIm Minkowski-Raum wird der kontravariante Orts-Vierervektor definiert durch
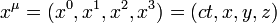 .
.Der metrische (genauer: pseudometrische) Tensor lautet in einer Konvention, die vor allem in der Quantenfeldtheorie verwendet wird (Signatur -2, also +---)
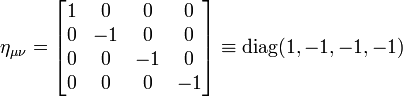 .
.
In einer Konvention, die hauptsächlich in der Allgemeinen Relativitätstheorie benutzt wird (Signatur +2, also -+++), schreibt man
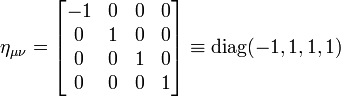 .
.
In der Allgemeinen Relativitätstheorie ist der metrische Tensor ortsabhängig und bildet daher ein Tensorfeld, da die Krümmung der Raumzeit an verschiedenen Punkten meist verschieden ist.
-
Wikimedia Foundation.

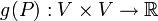
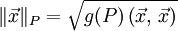
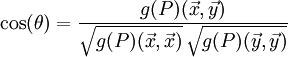
![L_{[a,b]}(\gamma)
= \int_a^b \sqrt{ g\bigl(\gamma(t)\bigr) \Bigl(\,\vec x(t),\,\vec x(t)\, \Bigr)}\,\mathrm{d}t
= \int_a^b \|\dot\gamma(t)\|_{\gamma(t)}\,\mathrm{d}t](/pictures/dewiki/57/996b2922c174fa838e074a6685fbea78.png)