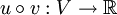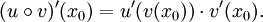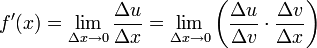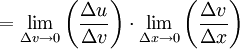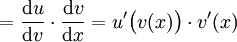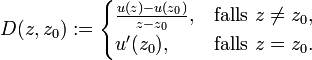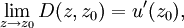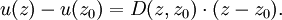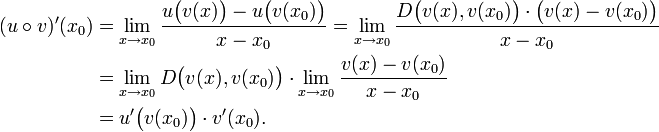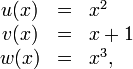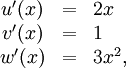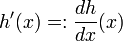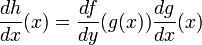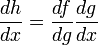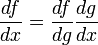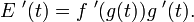Verkettung von Funktionen

Die Kettenregel ist eine der Grundregeln der Differentialrechnung. Sie trifft Aussagen über die Ableitung einer Funktion, die sich selbst als Verkettung von zwei differenzierbaren Funktionen darstellen lässt. Kernaussage der Kettenregel ist dabei, dass eine solche Funktion selbst wieder differenzierbar ist und man ihre Ableitung erhält, indem man die beiden miteinander verketteten Funktionen separat ableitet und – ausgewertet an den richtigen Stellen – miteinander multipliziert. Die Kettenregel lässt sich verallgemeinern auf Funktionen, die sich als Verkettung von mehr als zwei differenzierbaren Funktionen darstellen lassen. Auch eine solche Funktionen ist wiederum differenzierbar, ihre Ableitung erhält man durch Multiplikation der Ableitungen aller ineinander verschachtelten Funktionen.

Die Kettenregel bildet einen Spezialfall der verallgemeinerten Kettenregel für den eindimensionalen Fall. Sie ist außerdem das Gegenstück zur Integration durch Substitution in der Integralrechnung.

Mathematische Formulierung

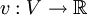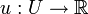Seien U, V offene Intervalle, $v: V \rightarrow \mathbb{R}$ und $u: U \rightarrow \mathbb{R}$ Funktionen mit 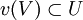$v(V) \subset U$. Die Funktion v sei im Punkt 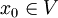$x_0 \in V$ differenzierbar und u sei im Punkt 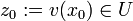$z_0 := v(x_0) \in U$ differenzierbar. Dann ist die zusammengesetzte Funktion

$u \circ v: V \rightarrow \mathbb{R}$

im Punkt x₀ differenzierbar und es gilt:

$(u \circ v)'(x_0) = u'\big(v(x_0)\big)\cdot v'(x_0).$

Im Zusammenhang mit der Kettenregel nennt man u auch die äußere, v die innere Funktion von f.

Praktische Merkregel: Die Ableitung einer verketteten Funktion ist die "äußere Ableitung" u' - ausgewertet an der Stelle v(x₀) - mal der Ableitung der inneren Funktion v', ausgewertet an der Stelle x₀, oder kurz: "Äußere Ableitung mal innere Ableitung".

Beispiel

Es wird die durch f(x) = (x³ + 1)² definierte Funktion f betrachtet. f lässt sich darstellen als Verkettung der Funktion

u(x) = x²

mit der Funktion

v(x) = x³ + 1,

denn es gilt f(x) = u(v(x)). In der Terminologie der Kettenregel bezeichnet u die äußere, v die innere Funktion. Für die Anwendung der Kettenregel benötigen wir die Ableitungen u' ("äußere Ableitung") und v' ("innere Ableitung"):

u'(x) = 2x

und

v'(x) = 3x².

Da sowohl u als auch v differenzierbar sind, ist nach der Kettenregel auch 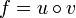$f = u \circ v$ differenzierbar, und es gilt für ihre Ableitung: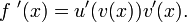

$f\ '(x) = u'(v(x)) v'(x).$

Nun ist u'(v(x)) = 2(x³ + 1), so dass wir insgesamt erhalten:

$f\ '(x) = 2(x^3 + 1) 3x^2$

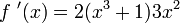
Es ist üblich, der Übersicht halber in der äußeren Funktion die unabhängige Variable mit dem Funktionssymbol der inneren Funktion zu identifizieren, obwohl die Benennung der Variable prinzipiell keine Rolle spielt. In diesem Sinne verwendet man die Variable v sozusagen als Abkürzung für den Term, der in der Klammer steht. In dieser Schreibweise ist dann die äußere Funktion durch

u(v) = v²,

die innere durch

v(x) = x³ + 1

gegeben. Man beachte, dass die Darstellung einer Funktion als Verkettung einer äußeren mit einer inneren Funktion keineswegs eindeutig sein muss. So lässt sich die Beispielfunktion auch als Verkettung der Funktionen u(x) = (x + 1)² und v(x) = x³ auffassen, denn auch für diese beiden Funktionen gilt:

u(v(x)) = (x³ + 1)² = f(x).

Die Anwendung der Kettenregel ist in diesem Fall rechnerisch aufwändiger, da zumindest der Term (x + 1)² ausmultipliziert werden muss.

Insgesamt lässt sich an diesem Beispiel die Kettenregel im Sinne der konstruktivistischen Didaktik selbst entdecken. Ausmultiplizieren ergibt:

f(x) = x⁶ + 2x³ + 1.

Nach Ableiten wird durch Ausklammern die innere Funktion v(x) = x³ + 1 herauspräpariert:

$f'(x) = 6x^5+6x^2 = 6x^2(x^3+1) = 2(x^3+1)\cdot 3x^2$.

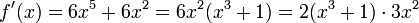Hieraus lässt sich dann die Kettenregel vermuten, die dann noch in ihrer Allgemeingültigkeit bewiesen werden muss.

Geometrische Veranschaulichung

Von x zum Funktionswert u(v(x)) kann man gelangen, indem man zuerst v(x) und dann u(v) berechnet. Die Funktion v(x) hat die Steigung v'(x) (innere Ableitung). Die Funktion u(v) hat die Steigung u'(v) (äußere Ableitung). Die Steigung von u(v(x)) ist u'(x) (Gesamtableitung).

Der Term 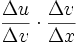${\Delta u \over \Delta v} \cdot {\Delta v \over \Delta x}$ entsteht dabei durch Erweiterung des Bruchs 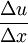${\Delta u \over \Delta x}$ mit Δv, also Multiplikation mit 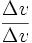${\Delta v \over \Delta v}$ und Umschreibung. Zu beachten ist hierbei: Die Verkettung von Funktionen ist etwas ganz anderes als die Multiplikation von Funktionen.

Für die Differenzenquotienten gilt (siehe Abbildung): ${\Delta u \over \Delta x} = {\Delta u \over \Delta v} \cdot {\Delta v \over \Delta x}$

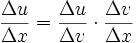
Durch den Grenzübergang Δx → 0 werden aus den Differenzenquotienten die Differentialquotienten. Aus der obigen Abbildung geht hervor: Geht Δx gegen Null, dann auch Δv.

Man erhält dann insgesamt für die Ableitung der verketteten Funktion:

$f'(x) = \lim_{\Delta x \rightarrow 0}{\Delta u \over \Delta x} = \lim_{\Delta x \rightarrow 0}\biggl({\Delta u \over \Delta v} \cdot {\Delta v \over \Delta x}\biggl)$

$= \lim_{\Delta v \rightarrow 0}\biggl({\Delta u \over \Delta v}\biggl) \cdot \lim_{\Delta x \rightarrow 0}\biggl({\Delta v \over \Delta x}\biggl)$

$= \frac{\mathrm du}{\mathrm dv} \cdot \frac{\mathrm dv}{\mathrm dx} = u'\big(v(x)\big)\cdot v'(x)$

Anmerkung: Die hier verwendete Schreibweise mit Differentialen (z. B. dx) nach Leibniz ist äquivalent zur obigen Schreibweise nach Lagrange, vgl. auch den letzten Absatz dieses Artikels.

Beweis

Sei

$D(z,z_0) := \begin{cases} \frac {u(z)-u(z_0)} {z-z_0}, & \text{falls } z \ne z_0, \\ u'(z_0), & \text{falls } z = z_0. \end{cases}$

Weil u in z₀ differenzierbar ist, gilt

$\lim_{z \to z_0} D(z,z_0) = u'(z_0),$

das heißt, D(z,z₀) ist bei z = z₀ stetig. Außerdem gilt für alle $z \in U$

$u(z)-u(z_0) = D(z,z_0)\cdot(z-z_0).$

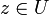
Daraus folgt

$\begin{align} (u \circ v)'(x_0) &= \lim_{x \to x_0}\frac{u\big(v(x)\big)-u\big(v(x_0)\big)}{x-x_0} = \lim_{x \to x_0}\frac{D\big(v(x),v(x_0)\big)\cdot\big(v(x)-v(x_0)\big)}{x-x_0} \\ &= \lim_{x \to x_0} D\big(v(x),v(x_0)\big)\cdot\lim_{x \to x_0}\frac{v(x)-v(x_0)}{x-x_0} \\ &= u'\big(v(x_0)\big)\cdot v'(x_0). \end{align}$

Verallgemeinerung auf mehrfache Verkettungen

Etwas komplizierter wird das Differenzieren, wenn mehr als zwei Funktionen verkettet sind. In diesem Fall wird die Kettenregel rekursiv angewendet. Beispielsweise ergibt sich bei Verkettung von drei Funktionen u, v und w

f(x) = u(v(w(x)))

die Ableitung

$f'(x) = u'(v(w(x)))\cdot (v(w(x)))' = u'(v(w(x))) \cdot v'(w(x)) \cdot w'(x)$.

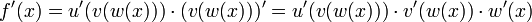Im Allgemeinen besitzt die Funktion

$f = u_1 \circ \cdots \circ u_n$

die Ableitung

$f'(x) = u_1' (u_2(\cdots(u_n(x)))) \cdot u_2'(u_3(\cdots(u_n(x)))) \cdots u_n'(x),$

wie sich durch vollständige Induktion beweisen lässt. Beim praktischen Berechnen der Ableitung multipliziert man also Faktoren, die sich folgendermaßen ergeben:

Den ersten Faktor erhält man dadurch, dass man die äußerste Funktion durch eine unabhängige Variable ausdrückt und ableitet. Anstelle dieser unabhängigen Variablen ist der Rechenausdruck für die restlichen (inneren) Funktionen einzusetzen. Der zweite Faktor wird entsprechend berechnet als Ableitung der zweitäußersten Funktion, wobei auch hier der Rechenausdruck für die zugehörigen inneren Funktionen einzusetzen ist. Dieses Verfahren setzt man fort bis zum letzten Faktor, der innersten Ableitung.

Als Beispiel kann wiederum die Funktion f(x) = (x³ + 1)² dienen. Diese lässt sich darstellen als Verkettung der drei Funktionen:

$\begin{array}{ccl} u(x) &=& x^2 \\ v(x) &=& x + 1 \\ w(x) &=& x^3, \end{array}$

denn es gilt:

u(v(w(x))) = u(w(x) + 1) = u(x³ + 1) = (x³ + 1)² = f(x).

Damit liefert die auf mehrfache Verkettungen verallgemeinerte Kettenregel mit

$\begin{array}{ccl} u'(x) &=& 2x \\ v'(x) &=& 1 \\ w'(x) &=& 3x^2, \end{array}$

die Ableitung

$f \ '(x) = u'(v(w(x)) v'(w(x)) w'(x) = 2 v(w(x)) \cdot 1 \cdot w'(x) = 2(x^3 + 1) 3x^2$.

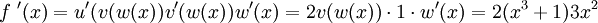Verallgemeinerung für höhere Ableitungen

Eine Verallgemeinerung für höhere Ableitungen ist wesentlich komplizierter und schwieriger zu beweisen. Sie ist als Formel von Faà di Bruno bekannt.

Abweichende Notationen in der Physik und anderen Wissenschaften

In vielen Naturwissenschaften wie der Physik, aber auch in der Ingenieurswissenschaft findet die Kettenregel breite Anwendung. Allerdings hat sich hier eine besondere Notation entwickelt, die von der mathematischen Notation der Kettenregel deutlich abweicht.

Vorstellung der Notation

In physikalischer Literatur wird für die Ableitung einer Funktion h nach der Variable x in der Regel die Schreibweise

$h'(x) =: \frac{dh}{dx}(x)$

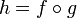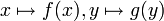bevorzugt. Ist h eine Verkettung zweier Funktionen: $h = f \circ g$ mit $x \mapsto f(x), y \mapsto g(y)$, so präsentiert sich die Kettenregel in dieser Notation:

$\frac{dh}{dx}(x) = \frac{df}{dy}(g(x)) \frac{dg}{dx}(x)$

Es ist zusätzlich gängige Konvention, die unabhängige Variable der Funktion f mit dem Funktionsymbol der inneren Funktion g zu identifizieren, dafür aber sämtliche Argumentklammern auszulassen:

$\frac{dh}{dx} = \frac{df}{dg} \frac{dg}{dx}$

Letztlich wird für die Verkettung 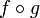$f \circ g$ kein neues Symbol eingeführt, sondern die gesamte Verkettung mit der äußeren Funktion f identifiziert: 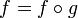$f = f \circ g$. Die Kettenregel nimmt dann das folgende Aussehen an:

$\frac{df}{dx} = \frac{df}{dg} \frac{dg}{dx}$

Formal stellt sich die Kettenregel hier als eine Erweiterung des "Bruches" df / dx mit dg dar, so dass es in physikalischer Fachliteratur (und auch in anderen Natur- und Ingenieurswissenschaften) gängig ist, die Kettenregel bei Anwendung nicht namentlich zu erwähnen. Stattdessen findet man oft Ersatzformulierungen, so ist etwa von der "Erweiterung von df / dx mit dg" die Rede, teilweise fehlt eine Begründung vollständig. Auch wenn dies für das ungeübte Auge nicht immer auf den ersten Blick erkennbar ist, steckt hinter all diesen Formulierungen ausnahmslos die Kettenregel der Differenzialrechnung.

Obwohl die vorgestellte Notation mit einigen mathematischen Konventionen bricht, erfreut sie sich großer Beliebtheit und weiter Verbreitung, da sie es ermöglicht, mit Ableitungen (zumindest rein formal) wie mit "normalen Brüchen" zu rechnen. Viele Rechnungen gestaltet sie außerdem übersichtlicher, da Klammern entfallen und nur sehr wenige Symbole verwendet werden müssen. Vielfach stellt auch die durch eine Verkettung beschriebene Größe eine bestimmte physikalische Variable dar (z.B. eine Energie oder eine elektrische Spannung), für die ein bestimmter Buchstabe "reserviert" ist (etwa E für Energie und U für Spannung). Die obige Notation ermöglicht es, diesen Buchstaben in der gesamten Rechnung durchgängig zu verwenden.

Beispiel

Die kinetische Energie eines Körpers hängt von seiner Geschwindigkeit v ab: E = f(v). Hängt die Geschwindigkeit wiederum von der Zeit t ab, v = g(t), so ist auch die kinetische Energie des Körpers eine Funktion der Zeit, die durch die Verkettung

E(t) = f(g(t))

beschrieben wird. Möchten wir die Änderung der kinetischen Energie nach der Zeit berechnen, so gilt nach der Kettenregel

$E\ '(t) = f\ '(g(t)) g\ '(t).$

In physikalischer Literatur würde man die letzte Gleichung in folgender (oder ähnlicher) Gestalt vorfinden:

$\frac{dE}{dt} = \frac{dE}{dv}\frac{dv}{dt}.$

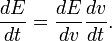
Klarer Vorteil ist die durchgängige Verwendung von Funktionssymbolen, deren Buchstaben mit denen der zugrunde liegenden physikalisch relevanten Größe (E für Energie, v für Geschwindigkeit) übereinstimmen.