- Liste von 23 mathematischen Problemen
-
Die hilbertschen Probleme sind eine Liste von 23, zum Zeitpunkt der Veröffentlichung, ungelösten Problemem der Mathematik. Sie wurden vom deutschen Mathematiker David Hilbert im Jahr 1900 beim Internationalen Mathematiker-Kongress in Paris vorgestellt.[1][2]
Geschichte
Hilbert war eingeladen worden, für den zweiten internationalen Mathematikerkongress (August 1900 in Paris) einen Vortrag zu halten. Er entschloss sich, keinen „Festvortrag“ zu halten, in dem er das bisher in der Mathematik Erreichte referieren und würdigen würde, sondern sein Vortrag sollte gewissermaßen einen programmatischen Ausblick auf die zukünftige Mathematik im kommenden Jahrhundert bieten. Diese Zielsetzung kommt in seinen einführenden Worten zum Ausdruck:
- Wer von uns würde nicht gerne den Schleier lüften, unter dem die Zukunft verborgen liegt, um einen Blick zu werfen auf die bevorstehenden Fortschritte unserer Wissenschaft und in die Geheimnisse ihrer Entwicklung während der künftigen Jahrhunderte! Welche besonderen Ziele werden es sein, denen die führenden mathematischen Geister der kommenden Geschlechter nachstreben? Welche neuen Methoden und neuen Tatsachen werden die neuen Jahrhunderte entdecken - auf dem weiten und reichen Felde mathematischen Denkens?[3]
Er nahm den Kongress daher zum Anlass, eine thematisch breit gefächerte Liste von ungelösten mathematischen Problemen zusammenzustellen. Bereits im Dezember 1899 begann er, sich über das Thema Gedanken zu machen. Am Anfang des neuen Jahres fragte er dann seinen engen Freund Hermann Minkowski sowie Adolf Hurwitz danach, welche Gebiete ein entsprechender Vortrag abdecken müsse. Endgültig niedergeschrieben hat Hilbert seine Liste allerdings erst kurzfristig vor dem Kongress. Im offiziellen Kongressprogramm ist sie deshalb nicht wiederzufinden.
Hilberts Vortrag fand im Rahmen der Kongressveranstaltungen zu „Bibliographie und Geschichte“ statt. Aus Zeitgründen stellte er zunächst nur zehn Probleme vor. Die Anwesenden erhielten eine französische Zusammenfassung der Liste, die wenig später in der schweizerischen Zeitschrift L'Enseignement Mathématique erschien. Der vollständige deutsche Originalartikel erschien kurze Zeit später in den Nachrichten der Königlichen Gesellschaft der Wissenschaften zu Göttingen[3] und im Jahr 1901 mit einigen Ergänzungen im Archiv der Mathematik und Physik.
2000 hat der deutsche Historiker Rüdiger Thiele in den Original-Notizen Hilberts ein 24. Problem entdeckt[4], das jedoch in der endgültigen Version der Liste fehlte und dem Gebiet der Beweistheorie zugeschrieben werden kann.
Probleme der Arbeit
Die Mathematik zur Jahrhundertwende war noch wenig gefestigt. Die Tendenz, Worte durch Symbole und vage Konzepte durch strenge Axiomatik zu ersetzen, war noch nicht sehr ausgeprägt und sollte erst der folgenden Mathematikergeneration erlauben, ihr Fach stärker zu formalisieren. Hilbert konnte noch nicht auf die Zermelo-Fraenkel-Mengenlehre, Begriffe wie den topologischen Raum und das Lebesgue-Integral oder die Church-Turing-These zurückgreifen. Die Funktionalanalysis, die unter anderem von Hilbert selbst mit der Einführung des nach ihm benannten Hilbert-Raumes begründet wurde, hatte sich als mathematisches Gebiet noch nicht von der Variationsrechnung abgetrennt.
Aus heutiger Sicht erfüllen die Formulierungen vieler Probleme deshalb nicht mehr die Anforderungen, die ein moderner Mathematiker an derartige Texte stellen würde. Fragen müssten so genau gestellt sein, dass sie eindeutig durch die Veröffentlichung eines Beweises gelöst werden könnten. In Hilberts Liste ist dies jedoch in vielen Fällen nicht möglich. Manche Probleme sind eher Aufforderungen, auf bestimmten Gebieten zu forschen, als konkrete Fragestellungen und bei anderen sind die Fragen zu vage gestellt, um genau sagen zu können, was Hilbert als Lösung angesehen hätte.
Ein Fehler, der zwar die Formulierung der Probleme nicht beeinträchtigt, aber dennoch zu Hilberts größten Irrtümern zählt, ist in der Einleitung des Artikels zu finden. Dort bringt er seine Überzeugung zum Ausdruck, dass jedes Problem grundsätzlich lösbar sein muss:
- „Diese Überzeugung von der Löslichkeit eines jeden mathematischen Problems ist uns ein kräftiger Ansporn während der Arbeit; wir hören in uns den steten Zuruf: Da ist das Problem, suche die Lösung. Du kannst sie durch reines Denken finden; denn in der Mathematik gibt es kein Ignorabimus!“
Diese Hoffnung sollte sich nicht erfüllen. Spätestens mit der Entdeckung des Gödelschen Unvollständigkeitssatzes und Turings Beweis, dass das Entscheidungsproblem nicht lösbar ist, kann dieser Denkansatz Hilberts als Irrtum betrachtet werden. Das entwertet die Liste jedoch nicht, denn auch negative Lösungen, wie zum Beispiel die vom zehnten Problem, führen mitunter zu großem Erkenntnisgewinn.
Einfluss der Liste
Hilberts Liste war dazu gedacht, die weitere Entwicklung der Mathematik zu beeinflussen. Begünstigt durch den Umstand, dass Hilbert zu den renommiertesten Mathematikern seiner Generation gehörte, ging dieser Plan auf: Es versprach erheblichen Ruhm, eines der Probleme auch in Teilen zu lösen, sodass sich immer mehr Mathematiker mit den Themen aus Hilberts Vortrag beschäftigten und somit – selbst wenn sie scheiterten – die entsprechenden Teilgebiete weiterentwickelten. Die Arbeit übte somit einen wesentlichen Einfluss auf die Entwicklung der Mathematik im 20. Jahrhundert aus.
Obwohl es mehrfach Versuche gab, diesen Erfolg zu wiederholen, hatte keine andere Sammlung von Problemen und Vermutungen einen vergleichbaren Einfluss auf die Entwicklung der Mathematik. Auch die Weil-Vermutungen, benannt nach dem Mathematiker André Weil, und eine ähnliche Liste von John von Neumann gelangten zu größerer Bekanntheit und im Jahr 2000 lobte das Clay Mathematics Institute Preisgelder von jeweils einer Million US-Dollar für die Lösung von sieben wichtigen Problemen aus (siehe Millennium-Probleme). Die Berühmtheit von Hilberts Artikel bleibt bisher jedoch einzigartig.
Die Probleme
An den Beginn seiner Liste stellte Hilbert Fragen der axiomatischen Mengenlehre und andere axiomatische Überlegungen. In seinen Augen war es besonders wichtig, dass sich die mathematische Gemeinschaft Klarheit über die Fundamente der Mathematik verschafft, um tiefer gehende Aussagen besser verstehen zu können. Es folgen einige Fragen der Zahlentheorie, die durch algebraische Themen und schließlich durch Probleme aus der Funktionentheorie ergänzt werden. Im Folgenden sind Probleme, die weitgehend gelöst sind, grün hinterlegt und solche, die noch ungelöst sind, rot.
Hilberts erstes Problem
Fragestellung: Gibt es eine überabzählbare Teilmenge der reellen Zahlen, die in ihrer Mächtigkeit echt kleiner ist als die reellen Zahlen?
Lösung: Unentscheidbar im klassischen Axiomensystem.
In der Mengenlehre gehen Mathematiker heute zumeist von ZFC, dem Zermelo-Fraenkelschen Axiomensystem mit Auswahlaxiom aus (letzteres wird oft auch weggelassen), das alle mathematischen Überlegungen formal fundiert. Man kann zeigen, dass auf dieser Grundlage viele Mengen dieselbe Mächtigkeit besitzen, so zum Beispiel die Menge der reellen Zahlen, die Menge der komplexen Zahlen, das Intervall [0, 1] oder die Potenzmenge der natürlichen Zahlen. Die Kontinuumshypothese besagt nun, dass alle Mengen, die nicht mehr abzählbar sind, das heißt nicht in eine 1:1-Beziehung mit den natürlichen Zahlen gebracht werden können, mindestens die Mächtigkeit der reellen Zahlen besitzen.
Kurt Gödel konnte 1939 zeigen, dass die Kontinuumshypothese zu ZFC relativ widerspruchsfrei ist: falls ZFC zu keinem Widerspruch führt, so bleibt diese Eigenschaft erhalten, wenn man das Axiomensystem um die Kontinuumshypothese ergänzt. Paul Cohen konnte schließlich 1963 zeigen, dass auch die Negation der Kontinuumshypothese relativ widerspruchsfrei zu ZFC ist, sie also nicht aus ZFC gefolgert werden kann. Daraus folgt, dass die Kontinuumshypothese unabhängig vom klassischen Axiomensystem ist und bei Bedarf als neues Axiom eingesetzt werden kann.
Eine verwandte Frage, die Hilbert in der Formulierung seines Problems hinzugefügt hat, ist, ob eine Wohlordnung der reellen Zahlen existiert. Ernst Zermelo konnte beweisen, dass dies auf Grundlage von ZFC tatsächlich der Fall ist, auch wenn eine solche Wohlordnung nicht explizit angegeben werden kann. Ohne das Auswahlaxiom, also im System ZF, kann die Aussage nicht gezeigt werden.
→ Hauptartikel: Kontinuumshypothese
Hilberts zweites Problem
Fragestellung: Sind die arithmetischen Axiome widerspruchsfrei?
Lösung: Nach dem Unvollständigkeitssatz von Kurt Gödel kann diese Frage nicht mit Hilfe der arithmetischen Axiome beantwortet werden.
Giuseppe Peano hatte 1889 ein arithmetisches Axiomensystem beschrieben, das die Fundierung der Mathematik festlegen sollte. Hilbert war der Überzeugung, dass es damit möglich sein müsste zu zeigen, dass nur von dieser Grundlage ausgehend kein Widerspruch erzeugt werden kann. Diese Hoffnung zerstörte jedoch Kurt Gödel, als er 1930 mit seinem Unvollständigkeitssatz zeigte, dass dies nicht unter ausschließlicher Verwendung der Peano-Axiome möglich ist.
→ Hauptartikel: Hilbertprogramm
Hilberts drittes Problem
Fragestellung: Sind zwei beliebige Tetraeder mit gleichen Grundflächen und gleichen Höhen stets zerlegungsgleich oder lassen sie sich mit kongruenten Polyedern zu zerlegungsgleichen Körpern ergänzen?
Lösung: Weder ersteres noch letzteres ist der Fall.
Zwei Körper heißen zerlegungsgleich, wenn der eine sich so in endlich viele Teile zerlegen lässt, dass sich die einzelnen Teile wieder zum zweiten Körper zusammenfügen lassen. In der 2-dimensionalen Ebene gilt, dass Vielecke genau dann den gleichen Flächeninhalt besitzen, wenn sie zerlegungsgleich sind. Die Frage liegt also nahe, ob dieses Ergebnis auch im 3-dimensionalen Raum gilt.
Max Dehn, ein Schüler von Hilbert, konnte diese Frage bereits 1900, kurz nach der Veröffentlichung der 23 Probleme, mit „Nein“ beantworten. Er ordnete dazu jedem Polyeder eine Dehn-Invariante genannte Zahl zu. Diese hat die Eigenschaft, dass sie für zwei Polyeder genau dann gleich ist, wenn diese zerlegungsgleich sind. Mit der Beobachtung, dass jeder Würfel die Dehn-Invariante 0 und jedes regelmäßige Tetraeder eine von 0 verschiedene Dehn-Invariante besitzt, folgt dann die Aussage. Das Problem ist das erste von Hilberts Liste, das gelöst wurde.
- W. F. Kagan: Über die Transformation der Polyeder. In: Mathematische Annalen. Springer, Berlin 57.1903, S.421-424. ISSN 0025-5831
→ Hauptartikel: Hilberts drittes Problem
Hilberts viertes Problem
Fragestellung: Wie lassen sich die Metriken charakterisieren, in denen alle Geraden Geodäten sind?
Lösung: Heute gibt es zahlreiche Publikationen, die sich mit der Charakterisierung derartiger Metriken beschäftigen. Hilberts Problem ist jedoch zu vage gestellt, um eine klare Lösung angeben zu können.
Über 2000 Jahre lang wurde Geometrie anhand der fünf Axiome von Euklid gelehrt. Gegen Ende des 19. Jahrhunderts begann man, zu untersuchen, was das Hinzufügen und Entfernen verschiedener Axiome für Konsequenzen hat. So untersuchte Lobatschewski eine Geometrie, in der das Parallelenaxiom nicht gilt, und Hilbert betrachtete ein System, in dem das Archimedische Axiom fehlte. In seinen 23 Problemen forderte er schließlich zu einer „Aufstellung und systematischen Behandlung der [...] Geometrien“ auf, die einem bestimmten Axiomensystem genügen, in dem insbesondere die kürzeste Verbindung zweier Punkte stets die Gerade zwischen den Punkten ist.
Bereits 1901 konnte Georg Hamel, ein Schüler von Hilbert, in seiner Dissertation wichtige Aussagen über entsprechende Systeme zeigen, die er 1903 veröffentlichte. In den kommenden Jahrzehnten wurden immer wieder Arbeiten publiziert, die weitere Ergebnisse zu Hilberts viertem Problem beisteuerten.
→ Hauptartikel: Hilberts viertes Problem
Hilberts fünftes Problem
Fragestellung: Können zu einer beliebigen, lokal euklidischen, topologischen Gruppe Koordinaten so gewählt werden, dass sie die Struktur einer Lie-Gruppe besitzen?
Lösung: Ja.
Sophus Lie und Felix Klein bemühten sich am Ende des 19. Jahrhunderts, die Geometrie mit gruppentheoretischen Mitteln zu axiomatisieren, gingen dabei jedoch von Voraussetzungen über die Differenzierbarkeit gewisser Funktionen aus. Hilbert fragte sich nun, in welcher Weise die Theorie auch ohne diese Voraussetzungen noch Bestand hat. Da sich das Gebiet der algebraischen Topologie erst im 20. Jahrhundert entwickelt hat, hat sich die Formulierung des Problems mit der Zeit gewandelt. Hilberts ursprüngliche Fassung bezog sich nur auf kontinuierliche Transformationsgruppen.
Eine weitere Formulierung des Problems ist die Folgende: Betrachtet wird eine Gruppe G mit neutralem Element e, eine offene Menge U im euklidischen Raum, die e enthält und eine stetige Abbildung F: V × V → U, die auf der offenen Teilmenge V von U die Gruppenaxiome erfüllt. Die Frage ist dann, ob F auf einer Umgebung von e glatt, also unendlich oft differenzierbar ist. Nachdem John von Neumann und Lew Pontrjagin Spezialfälle lösen konnten, gelang Andrew Gleason, Deane Montgomery und Leo Zippin in den 1950er Jahren die endgültige Klärung des Problems.
- A. Gleason: Groups without small subgroups. In: Annals of Mathematics. University Press, Princeton 56.1952, S.193-212. ISSN 0003-486X
- D. Montgomery, L. Zippin: Small groups of finite-dimensional groups. In: Annals of Mathematics. University Press, Princeton 56.1952, S.213-241. ISSN 0003-486X
→ Hauptartikel: Hilberts fünftes Problem
Hilberts sechstes Problem
Fragestellung: Wie kann die Physik axiomatisiert werden?
Lösung: Unbekannt.
Ursprünglich ging es Hilbert in diesem Punkt um eine axiomatische Behandlung der Wahrscheinlichkeitstheorie und der Mechanik. Inzwischen gibt es mit der Relativitätstheorie und der Quantenphysik weitaus tiefere Einblicke in die Struktur des Universums, eine allgemeine axiomatische Formulierung der Physik ist aber nicht in Sicht.
→ Hauptartikel: Physik
Hilberts siebtes Problem
Fragestellung: Ist die Potenz αβ immer transzendent, wenn α algebraisch (α ≠ 0, α ≠ 1) und β irrational und algebraisch ist?
Lösung: Ja.
Eine Zahl heißt algebraisch, wenn sie Nullstelle eines Polynoms mit ganzzahligen Koeffizienten ist, andernfalls heißt sie transzendent. Die Wurzel aus 2 ist beispielsweise eine Zahl, die nicht mehr rational ist, als Nullstelle von x² - 2 aber immer noch algebraisch. Reelle Zahlen, die nicht mehr algebraisch sind (und damit transzendent), sind zum Beispiel die Kreiszahl π oder die Eulersche Zahl e.
Zu Hilberts Zeiten gab es bereits einige Ergebnisse über die Transzendenz verschiedener Zahlen. Obiges Problem erschien ihm besonders schwierig und er erhoffte sich aus seiner Lösung tiefere Erkenntnisse über die Natur der Zahlen. Nachdem das Problem zunächst für einige Spezialfälle gelöst wurde, konnte Alexander Gelfond 1934 die Aussage beweisen. Kurze Zeit später hat Theodor Schneider den Satz weiter verbessert, sodass die Antwort auf Hilberts siebtes Problem heute als Satz von Gelfond-Schneider bekannt ist.
Hilberts siebtes Problem ist ein Spezialfall der weiter gefassten geometrischen Behauptung: Wenn in einem gleichschenkligen Dreieck das Verhältnis der Winkel an der Basis zum Winkel an der Spitze irrational und algebraisch ist, dann ist das Verhältnis zwischen Basis und Schenkel transzendent.
- Alexander Gelfond: On Hilbert's seventh problem. In: Doklady Akademii Nauk SSSR. Izvestija Akedemii Nauk, Moskau 2.1934, S.177-182. ISSN 0002-3264
- Th. Schneider: Transzendenzuntersuchungen periodischer Funktionen. Bd I. Transzendenz von Potenzen. In: Journal für die reine und angewandte Mathematik. de Gruyter, Berlin 172.1934, S.177-182. ISSN 0075-4102
→ Hauptartikel: Satz von Gelfond-Schneider
Hilberts achtes Problem
Fragestellung: Besitzen alle nichttrivialen Nullstellen der riemannschen Zetafunktion den Realteil ½? Ist jede gerade Zahl größer als 2 als Summe zweier Primzahlen darstellbar?
Lösung: Unbekannt.
Die beiden genannten Probleme sind als Riemannsche Vermutung und Goldbachsche Vermutung bekannt und zwei der populärsten ungelösten Probleme der Mathematik. Da für die erste Frage bereits Milliarden von Nullstellen mit Realteil ½ berechnet wurden und dabei keine gefunden wurde, die die Vermutung falsifizieren würde, und die zweite Frage schon bis zu Zahlen der Größenordnung 1017 geprüft wurde, liegt die Vermutung nahe, dass beide Fragen mit ja beantwortet werden können. Formale Beweise dazu konnte man aber bis heute (2009) nicht finden.
Unter der Überschrift „Primzahlenprobleme“ hat Hilbert noch mehr Fragen zusammengetragen, die mit Primzahlen in Verbindung stehen. So nennt er zum Beispiel die (ebenfalls bis heute noch ungelöste) Frage, ob es unendlich viele Primzahlzwillinge gibt und ob die Gleichung ax + by + c = 0 mit ganzzahligen, teilerfremden Koeffizienten a, b und c von Primzahlen erfüllt werden kann.
→ Hauptartikel: Riemannsche Vermutung, Goldbachsche Vermutung
Hilberts neuntes Problem
Fragestellung: Wie kann das Reziprozitätsgesetz auf beliebige Zahlkörper verallgemeinert werden?
Lösung: Nur im abelschen Fall bekannt.
Bereits seit Fermat war bekannt, dass die Primfaktorzerlegung jeder Zahl, die um 1 größer ist als eine Quadratzahl, nur aus der Zahl 2 sowie Zahlen der Form 4k + 1 besteht. Eine allgemeinere Form, die das Legendre-Symbol benutzt, konnte Gauß beweisen:
Dieses Reziprozitätsgesetz sollte nun auf allgemeine Zahlkörper verallgemeinert werden. Mit der Entwicklung der Klassenkörpertheorie standen die dazu nötigen Mittel zur Verfügung, sodass Emil Artin das Problem im abelschen Fall lösen konnte – auch wenn es ihm noch nicht gelang, eine explizite Formel anzugeben. Dies holte Igor Safarevic 1948 nach. Eine weitere Verallgemeinerung auf den nicht-abelschen Fall konnte bisher nicht erreicht werden.
→ Hauptartikel: Quadratisches Reziprozitätsgesetz
Hilberts zehntes Problem
Fragestellung: Gibt es ein Verfahren, das für eine beliebige diophantische Gleichung entscheidet, ob sie lösbar ist?
Lösung: Nein.
Diophantische Gleichungen sind Gleichungen der Form f(x1, x2, ..., xn) = 0, wobei f ein Polynom in mehreren Variablen und mit ganzzahligen Koeffizienten ist und nur ganze Zahlen als Lösungen betrachtet werden. Ein bekanntes Beispiel ist die Gleichung x² + y² - z² = 0, die mit dem Satz des Pythagoras zusammenhängt. Diophantische Gleichungen spielen in der Geschichte der Mathematik eine wichtige Rolle, und viele große Mathematiker haben sich intensiv mit solchen Formeln beschäftigt.
Zwar konnten immer wieder Spezialfälle gelöst werden, doch eine allgemeine Lösung schien den Mathematikern im 19. Jahrhundert unerreichbar fern. Deswegen fragte Hilbert lediglich, wie man überprüfen kann, ob eine gegebene diophantische Gleichung überhaupt ganzzahlige Lösungen besitzt, ohne diese genau angeben zu können. Auch dieses Problem ist jedoch noch so schwer, dass Juri Matijassewitsch erst 1970 beweisen konnte, dass ein solches Verfahren für den allgemeinen Fall nicht existiert.
- Juri W. Matijassewitsch: Enumerable sets are Diophantine. In: Soviet mathematics Doklady. American Mathematical Society, Providence RI 11.1970, S.354-357. ISSN 0197-6788
→ Hauptartikel: Diophantische Gleichung
Hilberts elftes Problem
Fragestellung: Wie kann die Theorie der quadratischen Formen auf beliebige algebraische Zahlkörper verallgemeinert werden?
Lösung: Die Theorie wurde im 20. Jahrhundert umfangreich ausgebaut.
Eine quadratische Form ist eine Funktion der Form q(x) = xtAx, wobei x ein Vektor ist und A eine symmetrische Matrix. In den Jahrzehnten nach Hilberts Vortrag sind zahlreiche Ergebnisse veröffentlicht worden, die sich eingehend mit dem Thema beschäftigen. Als zentrales Ergebnis zählt dabei das Lokal-Global-Prinzip, das Helmut Hasse 1923 formulierte.
→ Hauptartikel: Quadratische Form
Hilberts zwölftes Problem
Fragestellung: Wie lässt sich der Satz von Kronecker-Weber auf beliebige Zahlkörper verallgemeinern?
Lösung: Unbekannt.
Der Satz von Kronecker-Weber besagt, dass die maximale abelsche Erweiterung des Körpers der rationalen Zahlen durch Adjunktion aller Einheitswurzeln entsteht. Der Verallgemeinerung dieses Satzes maß Hilbert eine große Bedeutung zu. Zwar gab es auf dem Gebiet im 20. Jahrhundert viele Fortschritte, zu einer Lösung von Hilberts zwölftem Problem kam es jedoch noch nicht.
→ Hauptartikel: Hilberts zwölftes Problem
Hilberts dreizehntes Problem
Fragestellung: Kann die Lösung der Gleichung x7 + ax3 + bx2 + x + 1 = 0 mit Hilfe einer endlichen Zahl von stetigen Funktionen konstruiert werden, die von zwei Variablen abhängen?
Lösung: Ja.
Eine allgemeinere Version dieser Frage ist: Gibt es stetige Funktionen in drei Variablen, die nicht als Verkettung von endlich vielen stetigen Funktionen in zwei Variablen dargestellt werden können? Andrei Kolmogorow und Wladimir Arnold konnten 1957 zeigen, dass dies in der Tat der Fall ist und widersprachen somit Hilbert, der in seinem Vortrag ein anderes Ergebnis vorhergesagt hatte.
→ Hauptartikel: Hilberts dreizehntes Problem
Hilberts vierzehntes Problem
Fragestellung: Sind bestimmte Ringe endlich erzeugt?
Lösung: Nein.
Im vierzehnten Problem beschreibt Hilbert spezielle Ringe: Dabei sei K[x1, ..., xn] ein Polynomring über einem Körper K, L ein Unterkörper des Körpers der rationalen Funktionen in n Variablen und R sei der Schnitt
Die Frage ist dann, ob die so konstruierten Ringe stets endlich erzeugt sind, also ob es eine endliche Teilmenge des Ringes gibt, die R erzeugen.
Bis in die 1950er Jahre konnte man von einigen Spezialfällen, insbesondere den Fällen n = 1 und n = 2 nachweisen, dass die so konstruierten Ringe tatsächlich endlich erzeugt sind. Die Ergebnisse legten also nahe, dass diese Aussage auch für alle Ringe der beschriebenen Art gelten könnte. Überraschend kam deshalb das Ergebnis von Masayoshi Nagata, der 1957 ein Gegenbeispiel angab, bei dem dies nicht der Fall ist, und somit das Problem negativ löste.
- Masayoshi Nagata: On the 14-th problem of Hilbert. In: American Journal of Mathematics. The Johns Hopkins University Press, Baltimore 81.1959, S.766-772. ISSN 0002-9327
→ Hauptartikel: Hilberts vierzehntes Problem
Hilberts fünfzehntes Problem
Fragestellung: Wie kann Schuberts Abzählungskalkül konkretisiert und formal begründet werden?
Lösung: Die Ergebnisse von Schubert sind in der Mitte des 20. Jahrhunderts gut verstanden worden.
Mit der Weiterentwicklung der algebraischen Geometrie standen nach und nach mathematische Hilfsmittel zur Verfügung, mit denen Schuberts Arbeit formalisiert werden konnte.
→ Hauptartikel: Schuberts Abzählungskalkül
Hilberts sechzehntes Problem
Fragestellung: Was kann über die gegenseitige Lage von algebraischen Kurven ausgesagt werden?
Lösung: Es konnten verschiedene Ergebnisse erzielt werden, viele Fragen bleiben aber offen.
Algebraische Kurven sind Teilmengen der Ebene, die durch Polynomgleichungen bestimmt werden. Dazu gehören zum Beispiel der Einheitskreis (x² + y² = 1) oder einfache Geraden (ax + b = y). Carl Harnack konnte 1876 zeigen, dass solche Mengen bei Polynomen vom Grad n (auch Kurven n-ter Ordnung genannt) aus höchstens ½(n - 1)(n - 2) + 1 Teilen bestehen können. Er konnte außerdem Beispiele konstruieren, die diese Maximalzahl auch erreichen („M-Kurven“).
Hilbert stellte fest, dass diese Teile nicht beliebig in der Ebene angeordnet sein können. So vermutete er beispielsweise, dass die elf Komponenten von M-Kurven sechster Ordnung immer so liegen, dass neun Komponenten sich im Inneren einer Schleife befinden und die letzte Komponente außerhalb dieser Schleife verläuft (oder umgekehrt) und forderte im ersten Teil des sechzehnten Problems dazu auf, Zusammenhänge dieser Art näher zu untersuchen.
Dies geschah mit der Entwicklung der Topologie der reellen algebraischen Mannigfaltigkeiten. Die von Hilbert ausgesprochene Vermutung konnte zum ersten Mal in den 1930er Jahren von Ivan Petrovsky bewiesen werden. Andere Resultate beziehen sich auf das dreidimensionale Äquivalent der Fragestellung: Karl Rohn hat bereits im 19. Jahrhundert gezeigt, dass algebraische Flächen vierter Ordnung aus höchstens zwölf Flächen bestehen können. Ob diese Grenze auch erreicht werden kann, ist bisher aber nicht bekannt.
→ Hauptartikel: Hilberts sechzehntes Problem
Hilberts siebzehntes Problem
Fragestellung: Kann jede rationale Funktion, die überall, wo sie definiert ist, nichtnegative Werte annimmt, als Summe von Quadraten von rationalen Funktionen dargestellt werden?
Lösung: Ja.
Mit algebraischen Mitteln konnte Emil Artin im Jahr 1927 das Problem lösen. Dazu betrachtete er eine bestimmte Klasse von Körpern und wies Eigenschaften nach, die ihn schließlich zu seinem Resultat führten.
- Emil Artin: Über die Zerlegung definiter Funktionen in Quadrate. In: Abhandlungen aus dem mathematischen Seminar der Universität Hamburg. Vandenhoeck & Ruprecht 5.1927, S.100-115. ISSN 0025-5858
→ Hauptartikel: Hilberts siebzehntes Problem
Hilberts achtzehntes Problem
Fragestellung: Gibt es nur endlich viele wesentlich verschiedene Raumgruppen im n-dimensionalen euklidischen Raum?
Lösung: Ja.
Der erste Teil von Hilberts achtzehntem Problem ist die mathematische Formulierung einer Frage aus der Kristallografie. Viele feste Stoffe besitzen auf atomarer Ebene eine kristalline Struktur, die sich mathematisch mit Bewegungsgruppen beschreiben lässt. Man konnte schon früh zeigen, dass es in der Ebene 17 und im Raum 230 wesentlich verschiedene Raumgruppen gibt. Ludwig Bieberbach konnte schließlich zeigen, dass diese Zahl auch in höheren Dimensionen stets endlich ist.
Im zweiten Teil des Problems fragt Hilbert, ob es im 3-dimensionalen Raum Polyeder gibt, die nicht als Fundamentalbereich einer Bewegungsgruppe auftreten, mit denen aber trotzdem der gesamte Raum lückenlos gekachelt werden kann. Dass dies der Fall ist, konnte erstmals Karl Reinhardt 1928 durch Angabe eines Beispiels zeigen.
Zuletzt fragt Hilbert nach der platzsparendsten Art, Kugeln im Raum anzuordnen. Bereits Johannes Kepler stellte 1611 die Vermutung auf, dass die kubisch-flächenzentrierte Packung und die hexagonale Packung optimal sind. Diese auch als keplersche Vermutung bekannte Aussage stellte sich jedoch als – wenn auch wenig überraschend – äußerst schwierig zu beweisen heraus. Erst 1998 veröffentlichte Thomas Hales einen computergestützten Beweis, der zur Zeit (2006) aber noch geprüft wird.
→ Hauptartikel: Hilberts achtzehntes Problem, Keplersche Vermutung
Hilberts neunzehntes Problem
Fragestellung: Sind alle Lösungen von Lagrangefunktionen analytisch?
Lösung: Unter gewissen Voraussetzungen ja.
Lagrangefunktionen sind spezielle partielle Differentialgleichungen, die besonders in der Physik Anwendung finden. Hilbert hatte mit einer gewissen Verwunderung beobachtet, dass es Differentialgleichungen gibt, die nur analytische Lösungen zulassen, also solche, die lokal durch Potenzreihen dargestellt werden können. Da verschiedene Resultate auch bei den wichtigen Lagrangefunktionen auf diese Eigenschaft hinwiesen nahm Hilbert die Frage danach in seinen Aufsatz auf.
Bereits im Jahr 1903 konnte Sergei Bernstein das Problem lösen, indem er die Analytizität einer gewissen Klasse von Differentialgleichungen bewies, die auch die fraglichen Gleichungen umfassen, unter der Voraussetzung, dass die dritten Ableitungen der Lösungen existieren und beschränkt sind. Später konnte Ivan Petrovsky das Ergebnis verschärfen und somit eine noch umfassendere Lösung zum neunzehnten Problem liefern.
→ Hauptartikel: Hilberts neunzehntes Problem
Hilberts zwanzigstes Problem
Fragestellung: Unter welchen Bedingungen besitzen Randwertprobleme Lösungen?
Lösung: Die Existenz einer Lösung kann nicht in jedem Fall durch eine Beschränkung der Randwerte gesichert werden.
Das zwanzigste Problem hängt eng mit dem neunzehnten zusammen und hat ebenfalls direkten Bezug zur Physik. Inzwischen gibt es umfangreiche Resultate zum Thema, sodass das Problem als gelöst angesehen werden kann.
→ Hauptartikel: Hilberts zwanzigstes Problem
Hilberts einundzwanzigstes Problem
Fragestellung: Gibt es stets ein System von fuchsschen Differentialgleichungen bei gegebenen Singularitäten und gegebener Monodromiegruppe?
Lösung: Nein.
Nachdem die Frage zunächst für einige Spezialfälle positiv beantwortet werden konnte, gelang es Andrei Bolibruch 1994 schließlich, im allgemeinen Fall das Gegenteil zu beweisen.
- D. V. Anosov, A. A. Bolibruch: Aspects of Mathematics - The Riemann-Hilbert problem. Vieweg, Braunschweig 1994. ISBN 3-5280-6496-X
→ Hauptartikel: Riemann-Hilbert-Problem
Hilberts zweiundzwanzigstes Problem
Fragestellung: Wie können analytische Beziehungen mittels automorpher Funktionen uniformisiert werden?
Lösung: Für Gleichungen mit zwei Variablen gelöst, bei mehr Variablen gibt es noch offene Fragen.
Bei der Uniformisierung setzt man sich zum Ziel, algebraische Kurven in zwei Variablen zu parametrisieren, also die Variablen durch Funktionen zu ersetzen, die nur noch von einer Veränderlichen abhängen. So lässt sich beispielsweise der Einheitskreis, der durch x² + y² = 1 gegeben ist, parametrisieren, indem man für x und y jeweils cos α und sin α einsetzt.
Als Hilbert seine Probleme formulierte, gab es schon eine Teillösung von Henri Poincaré, die Hilbert jedoch noch nicht zufriedenstellte. 1907 konnte Poincaré das Problem schließlich zusammen mit Paul Koebe lösen - allerdings nur für den Fall mit 2 Variablen. Verallgemeinert man das Problem auf mehr als zwei Variablen, so gibt es immer noch ungeklärte Fragen auf diesem Gebiet.
→ Hauptartikel: Uniformisierung
Hilberts dreiundzwanzigstes Problem
Fragestellung: Wie können die Methoden der Variationsrechnung weiterentwickelt werden?
Lösung: Das Problem ist zu vage gestellt, um eine konkrete Lösung angeben zu können.
Die Variationsrechnung ist in Hilberts Worten „die Lehre vom Variieren der Funktionen“ und hatte in seiner Auffassung eine besondere Wichtigkeit. Deswegen formuliert er im letzten Teil seines Vortrags kein spezielles Problem mehr, sondern forderte allgemein zur Weiterentwicklung dieses Gebietes auf. Mit der Entwicklung und dem umfangreichen Ausbau der Funktionalanalysis wurde diesem Anliegen Hilberts im 20. Jahrhundert Rechnung getragen.
→ Hauptartikel: Variationsrechnung
"Hilberts vierundzwanzigstes Problem"
Hilberts 24. Problem ist ein mathematisches (wissenschaftstheoretisches) Problem, dessen Formulierung in Hilberts Nachlass gefunden wurde und als Ergänzung seiner Liste von 23 mathematischen Problemen gilt. Hilbert stellt dabei die Frage nach Kriterien beziehungsweise Beweisen dafür, ob ein Beweis der einfachste für ein mathematisches Problem ist.
→ Hauptartikel: Hilberts 24. Problem
Literatur
- David Hilbert: Mathematische Probleme. In: Nachrichten der Königlichen Gesellschaft der Wissenschaften zu Göttingen, mathematisch-physikalische Klasse. Vandenhoeck & Ruprecht 1900,3, S. 253-297. ISSN 0369-6650
- David Hilbert, Pavel S. Aleksandrov u. a.: Ostwalds Klassiker der exakten Wissenschaften. Bd 252. Die Hilbertschen Probleme. Akademische Verlagsgesellschaft Geest & Portig, Leipzig 1983 (4. Aufl.). ISBN 3-8171-3401-0
- Benjamin H. Yandell: The honors class - Hilbert's problems and their solvers. AK Peters, Natick 2001. ISBN 1-56881-141-1
Zitate im Text
- ↑ Die Mathematischen Probleme von David Hilbert 2000, Ina Kersten, Universität Bielefeld
- ↑ Mathematische Probleme 1900, David Hilbert (Vortrag)
- ↑ a b D. Hilbert: Mathematische Probleme - Vortrag, gehalten auf dem internationalen Mathematiker-Kongreß zu Paris 1900. In: Nachrichten von der Königl. Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse. S. 253-297 (1900) digitalisierter Originaltext
- ↑ Rüdiger Thiele: Hilbert´s Twenty-Fourth Problem, American Mathematical Monthly, Januar 2003 weblink
Weblinks
Wikimedia Foundation.


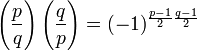
![R := L \cap K[x_1, ..., x_n].](/pictures/dewiki/101/e9e065f2836d9f04ae2439c0faf8ebcd.png)