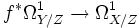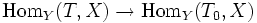- Verzweigungspunkt
-
Verzweigung ist ein mathematischer Begriff, der die Gebiete Algebra, algebraische Geometrie und komplexe Analysis miteinander verbindet.
Inhaltsverzeichnis
Namengebendes Beispiel
Es sei n > 1 eine natürliche Zahl und
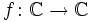 die Funktion
die Funktion 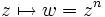 . Ist nun
. Ist nun 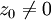 und U eine (hinreichend kleine) Umgebung von z0, so besteht das Urbild von U aus n Zusammenhangskomponenten, die durch eine Rotation um 2π / n, also Multiplikation mit einer n-ten Einheitswurzel auseinander hervorgehen. Bewegt sich
und U eine (hinreichend kleine) Umgebung von z0, so besteht das Urbild von U aus n Zusammenhangskomponenten, die durch eine Rotation um 2π / n, also Multiplikation mit einer n-ten Einheitswurzel auseinander hervorgehen. Bewegt sich 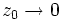 , so bewegen sich auch die Urbilder gegen 0, um dann für z0 = 0 zu einem einzigen Urbild zu verschmelzen. 0 ist also gewissermaßen der Verzweigungspunkt für die n Zweige. (Man beachte, dass die Zweige lokal bei 0 nicht getrennt sind, auch wenn man die 0 entfernt.)
, so bewegen sich auch die Urbilder gegen 0, um dann für z0 = 0 zu einem einzigen Urbild zu verschmelzen. 0 ist also gewissermaßen der Verzweigungspunkt für die n Zweige. (Man beachte, dass die Zweige lokal bei 0 nicht getrennt sind, auch wenn man die 0 entfernt.)Für den Übergang zu einer algebraischen Sichtweise sei nun g(w) eine holomorphe Funktion, die in einer Umgebung der 0 definiert ist. Hat g bei 0 eine k-fache Nullstelle, so hat die zurückgezogene Funktion
eine nk-fache Nullstelle. Dieses Zurückziehen lokal definierter holomorpher Funktionen entspricht einem Ringhomomorphismus
(Dabei bezeichnet
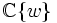 den Ring der Potenzreihen, deren Konvergenzradius positiv ist.) Die Nullstellenordnung ist eine diskrete Bewertung auf den beteiligten Ringen, und es gilt wie gesagt
den Ring der Potenzreihen, deren Konvergenzradius positiv ist.) Die Nullstellenordnung ist eine diskrete Bewertung auf den beteiligten Ringen, und es gilt wie gesagtDiese Eigenschaft ist charakteristisch für Verzweigungspunkte.
Verzweigung im Kontext von Erweiterungen bewerteter Körper
Es sei K ein Körper mit einer diskreten (Exponential-)Bewertung
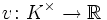 . Weiter seien
. Weiter seien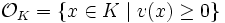 bzw.
bzw. 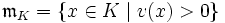
der Bewertungsring bzw. das Bewertungsideal von K, πK eine Uniformisierende, d. h. ein Erzeuger von
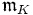 , und
, und 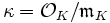 der Restklassenkörper. Weiter sei L eine endliche Erweiterung von K mit diskreter Bewertung
der Restklassenkörper. Weiter sei L eine endliche Erweiterung von K mit diskreter Bewertung 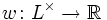 , die v fortsetzt, d. h. w | K = v. Schließlich seien
, die v fortsetzt, d. h. w | K = v. Schließlich seien 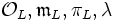 analog zu oben.
analog zu oben.Der Verzweigungsindex von L / K ist definiert als
Ist er gleich 1, so heißt die Erweiterung unverzweigt. Sein Gegenstück ist der Trägheitsgrad fw / v = [λ:κ].
Eigenschaften
- Ist die Erweiterung L / K separabel, und durchläuft w alle möglichen Fortsetzungen von v, so gilt die fundamentale Gleichung[1]
-
-
∑ ew / vfw / v = [L:K]. w / v
-
- Ist K darüber hinaus vollständig, so ist w eindeutig bestimmt[2] als
-
- und es gilt[3]
- ew / vfw / v = [L:K].
- Es seien nun K vollständig und L / K galoissch, und außerdem sei λ / κ separabel. (Diese Voraussetzungen sind beispielsweise für lokale Körper erfüllt.) Dann ist λ / κ sogar galoissch, und es gibt eine kurze exakte Sequenz[4]
-
- dabei bezeichnet man den Kern I als Trägheitsgruppe. Ihr Fixkörper T ist die maximale unverzweigte Teilerweiterung[5] von L / K, und im Fall endlicher Erweiterungen gilt
- Insbesondere gilt: Ist L / K unverzweigt, so ist
- Ist Knr die maximale unverzweigte Erweiterung (in einem separablen Abschluss Ksep von K), so gilt entsprechend
- Im Fall lokaler Körper ist letztere Gruppe kanonisch isomorph zu
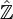 , hat also eine besonders einfache Struktur. Da die Galoisgruppe Gal(κsep / κ) im Frobenius-Automorphismus
, hat also eine besonders einfache Struktur. Da die Galoisgruppe Gal(κsep / κ) im Frobenius-Automorphismus
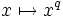 mit
mit 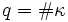
- einen kanonischen Erzeuger besitzt, gibt es auch in Gal(Knr / K) ein kanonisches Element, das ebenfalls als Frobenius-Automorphismus bezeichnet wird.
Verzweigung im Kontext von Erweiterungen von Dedekindringen
Es sei A ein Dedekindring mit Quotientenkörper K, L eine endliche separable Erweiterung von K und B der ganze Abschluss von A in L; B ist wieder ein Dedekindring.[6]
Einer der wichtigsten Spezialfälle ist
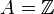 ,
, 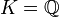 , L ein Zahlkörper und B sein Ganzheitsring.
, L ein Zahlkörper und B sein Ganzheitsring.Weiter sei
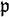 ein maximales Ideal von A. Dann lässt sich
ein maximales Ideal von A. Dann lässt sich 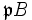 auf eindeutige Weise als Produkt von Potenzen verschiedener Primidealen von B schreiben:
auf eindeutige Weise als Produkt von Potenzen verschiedener Primidealen von B schreiben:Die Zahlen ei heißen Verzweigungsindizes, die Grade der Restklassenkörpererweiterungen
![f_i=[B/\mathfrak P_i:A/\mathfrak p]](/pictures/dewiki/99/c92c387765c290333f3f2d6474527a72.png) Trägheitsgrade.
Trägheitsgrade.- Ist ei = 1 und die Erweiterung der Restklassenkörper separabel, so heißt
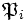 unverzweigt. (Im Fall von Zahlkörpern und Funktionenkörpern über endlichen Körpern ist die Restklassenkörperweiterung stets separabel.)
unverzweigt. (Im Fall von Zahlkörpern und Funktionenkörpern über endlichen Körpern ist die Restklassenkörperweiterung stets separabel.) - Ist fi = 1, so heißt
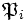 rein verzweigt.
rein verzweigt. - Sind alle
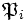 unverzweigt, so heißt
unverzweigt, so heißt 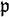 unverzweigt.
unverzweigt. 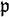 zerfällt dann in ein Produkt verschiedener Primideale.
zerfällt dann in ein Produkt verschiedener Primideale. - Sind alle Primideale (ungleich null) von K unverzweigt, so heißt die Erweiterung L / K unverzweigt.
Eigenschaften
- Ein Primideal
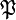 von L über einem Primideal
von L über einem Primideal 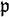 von K ist genau dann unverzweigt in dem hier definierten Sinne, wenn die Erweiterung L / K mit den durch
von K ist genau dann unverzweigt in dem hier definierten Sinne, wenn die Erweiterung L / K mit den durch 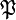 bzw.
bzw. 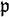 definierten Bewertungen unverzweigt im bewertungstheoretischen Sinne ist.
definierten Bewertungen unverzweigt im bewertungstheoretischen Sinne ist. - Es gilt die fundamentale Gleichung[7]
- Es gibt stets nur endlich viele verzweigte Primideale in K.[8] Ein Primideal in K ist genau dann verzweigt, wenn es die Diskriminante teilt;[9] ein Primideal in L ist genau dann verzweigt, wenn es die Differente teilt.[10]
- Es gibt keine unverzweigten Erweiterungen von
 .[11]
.[11] - Ist L / K eine Galoiserweiterung globaler Körper und
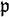 unverzweigt, so gibt es analog zum lokalen Fall für jedes Primideal
unverzweigt, so gibt es analog zum lokalen Fall für jedes Primideal 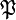 über
über 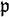 einen Frobenius-Automorphismus
einen Frobenius-Automorphismus 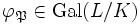 , der die Zerlegungsgruppe von
, der die Zerlegungsgruppe von 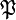 erzeugt. Er ist die Grundlage für das Artinsymbol der Klassenkörpertheorie.[12]
erzeugt. Er ist die Grundlage für das Artinsymbol der Klassenkörpertheorie.[12]
Unverzweigte Schemamorphismen
Es seien X und Y Schemata und
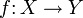 ein Morphismus lokal endlicher Präsentation. Dann heißt f unverzweigt, falls eine der folgenden äquivalenten Bedingungen erfüllt ist: [13]
ein Morphismus lokal endlicher Präsentation. Dann heißt f unverzweigt, falls eine der folgenden äquivalenten Bedingungen erfüllt ist: [13]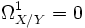
- Für einen (und damit für jeden) Morphismus
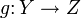 ist
ist
-
- surjektiv.
- Die Fasern von f über Punkten
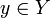 sind disjunkte Vereinigungen von Spektren endlicher separabler Körpererweiterungen von κ(y).
sind disjunkte Vereinigungen von Spektren endlicher separabler Körpererweiterungen von κ(y). - Die Diagonale
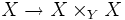 ist eine offene Einbettung.
ist eine offene Einbettung. - Ist T ein affines Schema und T0 ein abgeschlossenes Unterschema, das durch eine nilpotente Idealgarbe definiert wird, so ist die induzierte Abbildung
-
- injektiv.
Der Morphismus f heißt unverzweigt im Punkt
 , wenn es eine offene Umgebung U von x in X gibt, so dass f | U unverzweigt ist. Unverzweigtheit in einem Punkt x kann auch anders charakterisiert werden (es sei y = f(x)):[14]
, wenn es eine offene Umgebung U von x in X gibt, so dass f | U unverzweigt ist. Unverzweigtheit in einem Punkt x kann auch anders charakterisiert werden (es sei y = f(x)):[14]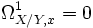
- Die Diagonale
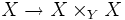 ist ein lokaler Isomorphismus bei x.
ist ein lokaler Isomorphismus bei x. 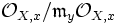 ist ein Körper, der eine endliche separable Erweiterung von κ(y) ist.
ist ein Körper, der eine endliche separable Erweiterung von κ(y) ist.
Die Unverzweigtheit von f im Punkt x hängt nur von der Faser f − 1(y) ab.
Eigenschaften
- Unverzweigte Morphismen sind lokal quasiendlich.[15]
- Ist Y zusammenhängend und
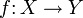 unverzweigt und separiert, so entsprechen die Schnitte von f eineindeutig den Zusammenhangskomponenten von X, die durch f isomorph auf Y abgebildet werden.[16]
unverzweigt und separiert, so entsprechen die Schnitte von f eineindeutig den Zusammenhangskomponenten von X, die durch f isomorph auf Y abgebildet werden.[16]
Bedeutung
Algebraische Geometrie
Ist X ein Schema über einem diskret bewerteten Körper K mit Bewertungsring V, so werden häufig Modelle von X über V betrachtet, d. h. Schemata
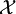 über V mit
über V mit 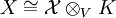 . Ist nun L / K eine unverzweigte Erweiterung und W der Bewertungsring von L, so ist der Morphismus
. Ist nun L / K eine unverzweigte Erweiterung und W der Bewertungsring von L, so ist der Morphismus 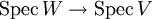 und damit auch der Morphismus
und damit auch der Morphismus 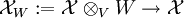 étale und surjektiv, folglich übertragen sich viele Eigenschaften von
étale und surjektiv, folglich übertragen sich viele Eigenschaften von 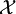 auf das Modell
auf das Modell 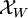 von XL.
von XL.Literatur
- Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin 1992. ISBN 3-540-54273-6.
- A. Grothendieck, J. Dieudonné: Éléments de géométrie algébrique. Publications mathématiques de l’IHÉS 4, 8, 11, 17, 20, 24, 28, 32 (1960–1967)
Quellen
- ↑ Neukirch, a.a.O., Satz (II.8.5), S. 173
- ↑ Neukirch, a.a.O., Theorem (II.6.2), S. 150
- ↑ Neukirch, a.a.O., Satz (II.6.8), S. 157
- ↑ Neukirch, a.a.O., Satz (II.9.9), S. 181
- ↑ Neukirch, a.a.O., Satz (II.9.11), S. 182
- ↑ Neukirch, a.a.O., Satz (I.8.1), S. 47
- ↑ Neukirch, a.a.O., Satz (I.8.2), S. 48
- ↑ Neukirch, a.a.O., Satz (I.8.4), S. 52
- ↑ Neukirch, a.a.O., Korollar (III.2.12), S. 213
- ↑ Neukirch, a.a.O., Theorem (III.2.6), S. 210
- ↑ Neukirch, a.a.O., Satz (III.2.18), S. 218
- ↑ Neukirch, a.a.O., Aufgabe I.9.2, S. 61, sowie Abschnitt VI.7, S. 424ff.
- ↑ EGA IV, 17.4.2, 17.2.2, 17.1.1, 17.3.1
- ↑ EGA IV, 17.4.1
- ↑ EGA IV, 17.4.3
- ↑ EGA IV, 17.4.9
Wikimedia Foundation.

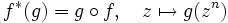
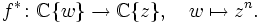
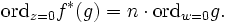
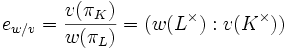
![w(x)=\frac1{[L:K]}v(N_{L/K}(x)),](/pictures/dewiki/55/70e27274af5f24ec9380cd5e616f19db.png)
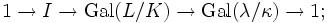
![[L:T]=\#I=e,\quad[T:K]=f.](/pictures/dewiki/50/2c760aebd06f46a4456f42b3ddba4f45.png)
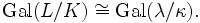
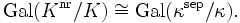
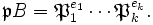
![[L:K]=\sum_{i=1}^k e_if_i.](/pictures/dewiki/102/f38d8ab074feea331c422225c7a11b4d.png)