Veränderungsrate

Änderungsraten einer zeitabhängigen Messgröße G beschreiben in Anwendungen der Mathematik wie der Experimentalphysik das Ausmaß der Veränderung von G in einem bestimmten Zeitraum im Verhältnis zur Dauer des Zeitraums. Man unterscheidet

• die „mittlere Änderungsrate“, hier ist der Bezugszeitraum die Zeit zwischen zwei Messungen, und
• die „momentane Änderungsrate“ oder „lokale Änderungsrate“, hier ist der Bezugszeitraum vernachlässigbar kurz („unendlich klein“).

Änderungsraten unterscheiden sich von Veränderungen und Differenzen dadurch, dass sie immer ein Verhältnis der Form „Größe pro Zeit“ sind. Damit hat die Änderungsrate einer Größe mit der Einheit 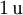$1\,\operatorname{u}$ die Einheit 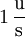$1\,\frac{\operatorname{u}}{\operatorname{s}}$ oder entsprechende Einheiten.

Berechnung und Verwendung

Mittlere Änderungsrate

Die mittlere Änderungsrate ist die durchschnittliche Änderung einer zeitabhängigen Messgröße G zwischen zwei Zeitpunkten t₁ und t₂. Berechnet wird sie als Quotient aus der Differenz der beiden Werte zu diesen Zeitpunkten ΔG = G(t₂) − G(t₁) und der Dauer Δt = t₂ − t₁ des Zeitraums:

Im Zeit-Größen-Diagramm (Schaubild) von G(t) ist die mittlere Änderungsrate zwischen t₁ und t₂ die Steigung der Sekante durch die Punkte (t₁ | G(t₁)) und (t₂ | G(t₂)) auf dem Schaubild.

Momentane Änderungsrate

Die momentane Änderungsrate ist die auf einen „Moment“ (sehr kurzen Zeitraum) bezogene Veränderung einer Messgröße G. Sie kann mathematisch als Ableitung 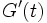$G^\prime(t)$ ihrer Zeit-G-Funktion G(t) dargestellt werden. Die experimentelle momentane Änderungsrate sollte (als selbständige Messgröße) jedoch von dieser mathematischen Ableitung unterschieden werden.

Änderungsraten in weiterem Sinn

Werden die Begriffe im übertragenen Sinn für andere Größen G(q) verwendet, die von einem anderen Parameter q als der Zeit abhängen, dann ist die mittlere Änderungsrate gleichbedeutend zu einem Differenzenquotienten, die momentane Änderungsrate gleichbedeutend zu einem Differentialquotienten der reellen Funktion G(q). Für eine mathematische Definition dieser Begriffe siehe den Grundlagenartikel Differentialrechnung.

Beispiele

• Bei einer geradlinigen Bewegung ist die Geschwindigkeit v(t) die momentane Änderungsrate der Zeit-Weg-Funktion s(t).

Der Quotient 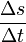$\frac{\Delta s}{\Delta t}$ aus der Veränderung Δs des Messwerts Weg in einer Zeitspanne Δt und dieser Zeitspanne ist die „mittlere Änderungsrate des Weges“ oder „Durchschnittsgeschwindigkeit“ in diesem Zeitraum. Durch experimentellen Grenzübergang - indem man immer kleinere Zeiträume betrachtet und die sich entwickelnde Tendenz feststellt - kommt man zu einer Annäherung an die momentane Änderungsrate der Zeit-Weg-Funktion, d.h. zur Momentangeschwindigkeit. Auch ein Radar-Geschwindigkeitsmessgerät misst die Momentangeschwindigkeit eines Fahrzeugs lediglich als mittlere Geschwindigkeit in einem allerdings sehr kleinen Zeitraum.

Der Artikel Geschwindigkeit führt dieses Beispiel aus und macht dabei die Unterschiede zwischen der experimentellen Änderungsrate und der mathematischen Ableitung deutlich. Siehe dazu auch Gerthsen (1992), S. 9f.

• In einem stromdurchflossenen Leiter kann die Stromstärke I(t) als Änderungsrate einer zeitabhängigen Ladungsfunktion Q(t) beschrieben werden.

Literatur

• Harro Heuser: Lehrbuch der Analysis Teil 1. 5. Auflage. Teubner-Verlag, 1988, ISBN 3-519-42221-2
• Christian Gerthsen, Hans O. Kneser, Helmut Vogel: Physik: ein Lehrbuch zum Gebrauch neben Vorlesungen. 16. Auflage. Springer-Verlag, 1992, ISBN 3-540-51196-2