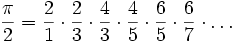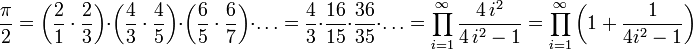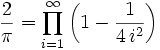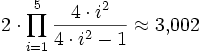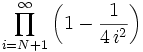Wallis-Produkt

Das wallissche Produkt, auch Wallis-Produkt, ist eine Produktdarstellung der Kreiszahl π, das heißt es handelt sich um ein Produkt mit unendlich vielen Faktoren, dessen Grenzwert Pi ist. Es wurde 1655 von dem englischen Mathematiker John Wallis entdeckt.

Formel

Üblich ist die Darstellung des Produktes in der Form:

$\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \dots$

Über eine Umformung ergibt sich die Kurzschreibweise des Wallisproduktes wie folgt:

$\frac{\pi}{2}= \left( \frac{2}{1} \cdot \frac{2}{3} \right) \cdot \left( \frac{4}{3} \cdot \frac{4}{5} \right) \cdot \left( \frac{6}{5} \cdot \frac{6}{7} \right) \cdot \dots = \frac{4}{3} \cdot \frac{16}{15} \cdot \frac{36}{35} \cdot \dots = \prod_{i=1}^\infty \frac{4 \, i^2}{4 \, i^2 - 1} = \prod_{i=1}^\infty\left(1+\frac{1}{4i^2-1}\right)$

Für den Kehrwert folgt:

$\frac 2{\pi} =\prod_{i=1}^\infty \bigg(1- \frac1{4 \, i^2}\bigg)$

Die Konvergenz dieses Produktes folgt aus der Konvergenz der unendlichen Reihe

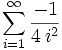$\sum_{i=1}^\infty \frac{-1}{4 \, i^2}$ bzw. $\sum_{i=1}^\infty \frac1{i^2}$

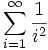
Konvergenzgeschwindigkeit

N	2*Produkt	2*Produkt / Pi	relativer Fehler
1	2,7	0,85	15%
2	2,8	0,91	9%
3	2,9	0,93	7%
10	3,07	0,976	2,4%
100	3,134	0,9975	0,25%
1000	3,1408	0,99975	0,025%
10000	3,14151	0,999975	0,0025%
100000	3,141585	0,9999975	0,00025%
$\lim_{n\to\infty}$	3,14159265...	1	0%

Zur effizienten Berechnung einer Näherung von Pi ist die Formel nicht geeignet. Berechnet man etwa die ersten 5 Terme des Wallischen Produkts und verdoppelt das Ergebnis, so erhält man als Näherung für Pi:

$2\cdot \prod_{i=1}^{5} \frac{4 \cdot i^2}{4 \cdot i^2 - 1} \approx 3{,}002$

Mit dieser Näherung konnte nicht einmal die erste Nachkommastelle korrekt bestimmt werden.

Nach Ausmultiplizieren der ersten 50 Terme ergibt sich ein Quotient aus zwei 160-stelligen Zahlen, der aber für Pi nur die Näherung 3,126 liefert, also nicht einmal 2 Nachkommastellen korrekt angibt. Da 3,126/3,14159 = 0,9950 ist, ist der relative Fehler etwa 0,5%. Die Konvergenzgeschwindigkeit ist langsamer als linear.

Die nebenstehende Tabelle gibt für einige ausgewählte Werte von N an, wie gut die Approximation von Pi ist, die man nach Ausmultiplizieren von N Termen im wallisschen Produkt erhält. Die Tabelle legt die Vermutung nahe, dass der Fehler nach Ausmultiplizieren von N Termen in etwa 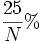$\frac{25}{N}\%$ beträgt (z.B. nach 100 Termen: 0,25% = $\tfrac{1}{400}$).

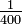Dies kann man auch durch folgende mathematische Überlegung beweisen: Der Quotient zwischen der Approximation und dem gewünschten Wert ist gleich dem unendlichen Produkt

$\prod_{i=N+1}^\infty \bigg(1- \frac1{4 \, i^2}\bigg)$

Mit Hilfe der Rechenregeln für Logarithmen, der Abschätzung 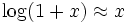$\log(1+x) \approx x$ (für kleine x) sowie durch Approximation einer unendlichen Summe durch ein Integral sieht man, dass dieses Produkt ungefähr den folgenden Wert hat:

$e^{\int_N^\infty \log\bigg(1- \frac1{4 \, x^2}\bigg) \,dx} \approx e^{\int_N^\infty -\frac1{4 \, x^2}\,dx} \approx e^{-\frac1{4 \, N}} \approx 1-\frac1{4 \, N}$.

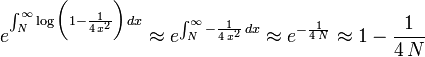Damit die ersten beiden Nachkommastellen richtig sind, braucht man demzufolge eine Genauigkeit von ca 0,3% (3,13/3,14 = 0,997), also etwa N = 60. Für 3 Nachkommastellen braucht man N = 600, für 4 Nachkommastellen N = 6000 etc.

Literatur

• Wallis, John: The arithmetic of infinitesimals (Übersetzung vom Latein ins Englische mit einem Vorwort von Jacqueline A. Stedall). 1. Auflage, Springer Verlag, Heidelberg, Berlin, New York 2004, ISBN 0-387-20709-0

Weblinks