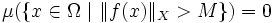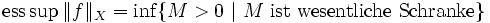Wesentlich beschränkt

Der Begriff des wesentlichen Supremums oder essentiellen Supremums wird in der Mathematik bei der Einführung der L^p-Räume für den Fall 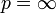$p = \infty$ als Erweiterung des Supremum-Begriffs benötigt. Da bei der Konstruktion dieser Funktionenräume Funktionen, die sich nur auf Nullmengen voneinander unterscheiden, als identisch betrachtet werden, kann man nur eingeschränkt von Funktionswerten in einzelnen Punkten sprechen. Der Begriff der beschränkten Funktion muss dementsprechend angepasst werden.

Definition

Seien 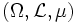$( \Omega,\mathcal{L},\mu)$ ein Maßraum und X ein Banachraum. Eine messbare Funktion 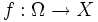$f: \Omega \rightarrow X$ heißt wesentlich beschränkt, wenn es eine Zahl 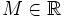$M \in \mathbb{R}$ gibt, so dass

$\mu ( \{ x \in \Omega \ | \ \| f(x) \|_X > M \} ) = 0$

ist, das heißt, es gibt eine Modifikation von f auf einer Nullmenge, so dass die entstehende Funktion im klassischen Sinne beschränkt ist. Jedes solche M wird eine wesentliche Schranke genannt. Als wesentliches Supremum, in Zeichen 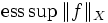$\mathrm{ess} \sup \|f\|_X$, bezeichnet man

$\mathrm{ess} \sup \|f\|_X = \inf \{ M > 0 \ | \ M \ \textrm{ist\ wesentliche\ Schranke} \}$

oder auch (für $A \subset \Omega$)

$\mathrm{ess} \sup_{x\in A} \|f(x)\|_X = \inf_{N\subset A, \mu(N)=0} \sup_{x\in A\setminus N} \|f(x)\|_X$.

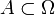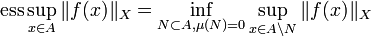Für eine stetige oder abschnittsweise stetige Funktion ergibt sich die Identität zum klassischen Supremum, falls μ das Lebesgue-Maß ist.

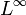$L^\infty$-Raum

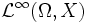Mit $\mathcal{L}^\infty (\Omega,X)$ wird die Menge aller wesentlich beschränkten Funktionen bezeichnet. Es sei mit 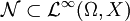$\mathcal{N}\subset\mathcal{L}^\infty (\Omega,X)$ die Menge der wesentlich beschränkten Funktionen mit Schranke 0 bezeichnet. Dann ist 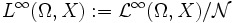$L^\infty (\Omega,X) := \mathcal{L}^\infty (\Omega,X) / \mathcal{N}$ die Menge der Äquivalenzklassen.

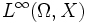$L^\infty (\Omega,X)$ ist ein linearer Raum mit Norm

$\| [f] \|_{L^\infty} = \mathrm{ess} \sup \|f\|_X , \ f \in [f]$.

Diese Norm ist unabhängig von der Wahl des Repräsentanten f in der Äquivalenzklasse [f]. Mit dieser Norm wird 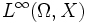$L^\infty (\Omega,X)$ zu einem Banachraum. In der mathematischen Literatur verzichtet man auf die eckigen Klammern, die für die Äquivalenzklasse von f stehen. In der Regel schreibt man einfach f und weist den Leser daraufhin, dass die auftretenden Gleichungen nur bis auf Nullmengen zu verstehen sind.

Beispiel

Betrachtet man die Dirichletsche Sprungfunktion auf $\R$ versehen mit dem Lebesgue-Maß, so ist das Supremum 1. Da die Menge der rationalen Zahlen aber eine Lebesgue-Nullmenge ist, ist das wesentliche Supremum 0.