Würfelnetz

Animation des Entfaltens eines Würfels

Würfelnetze sind meist auf Papier gezeichnete Bastelvorlagen zum Erstellen eines Würfels. Sie bestehen aus 6 identisch-quadratischen und zusammenhängenden Flächen, welche an einigen Stellen mit Kleberändern ergänzt wurden, um das spätere Kleben zu erleichtern.

Mathematisch gesehen gehören Würfelnetze zu den Hexominos, also eine Fläche aus 6 zusammenhängenden Quadraten. Jedoch stellen Würfelnetze nur eine Untergruppe der Hexominos dar: Die Würfelnetze müssen nämlich noch die Eigenschaft haben, sich zu einem Würfel zusammenzufalten.

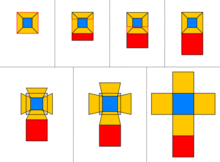
Insgesamt gibt es nur die elf folgenden Würfelnetze:

Alle 11 möglichen Würfelnetze

Weblinks

• Würfelnetze auf Matroids Matheplanet
• Gängiges Würfelnetz (PDF-Datei; 27 kB)