Würfel (Geometrie)

Regelmäßiges Hexaeder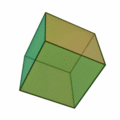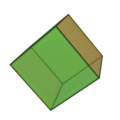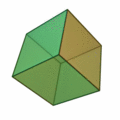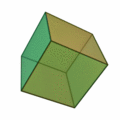
Art der Seitenflächen	Quadrate
Anzahl der Flächen	6
Anzahl der Ecken	8
Anzahl der Kanten	12
Schläfli-Symbol	{4,3}
dual zu	Oktaeder
Netz
Anzahl verschiedener Netze	11
Anzahl Kanten in einer Ecke	3
Anzahl Ecken einer Fläche	4

Der Würfel (von deutsch Wurf, weil er in Würfelspielen geworfen wird; auch regelmäßiges Hexaeder [hɛksaˈeːdər], von griech. hexáedron ‚Sechsflächner‘, oder Kubus, von lat. cubus ‚Würfel‘) ist einer der fünf platonischen Körper, genauer ein (dreidimensionales) Polyeder (Vielflächner) mit

• sechs (kongruenten) Quadraten als Begrenzungsflächen
• zwölf (gleichlangen) Kanten und
• acht Ecken, in denen jeweils drei Begrenzungsflächen zusammentreffen

Der Würfel ist ein spezielles (dreidimensionales) Parallelepiped (Parallelflach), ein spezieller (nämlich gleichseitiger) Quader sowie ein spezielles gerades quadratisches Prisma. Die Größe eines Würfels wird bereits durch die Angabe der Kantenlänge festgelegt.

Symmetrie

Zeichnung eines Würfels

Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Seiten sind untereinander gleichartig – ist der Würfel ein reguläres Polytop. Er hat

• drei vierzählige Drehachsen (durch die Mittelpunkte zweier gegenüberliegender Flächen),
• vier dreizählige Drehachsen (durch zwei diagonal gegenüberliegende Ecken),
• sechs zweizählige Drehachsen (durch die Mittelpunkte zweier diagonal gegenüberliegender Kanten) und
• neun Spiegelebenen (sechs Ebenen durch jeweils vier Ecken, drei Ebenen durch je vier Kantenmittelpunkte)
• 14 Drehspiegelungen (sechs um 90° mit den Ebenen durch je vier Kantenmittelpunkte und 8 um 60° mit Ebenen durch je sechs Kantenmitten)

und ist

• punktsymmetrisch (zum Mittelpunkt).

Für eine vierzählige Drehachse gibt es 3 Symmetrieoperationen (Drehung um 90°, 180° und 270°), für eine dreizählige Drehachse dementsprechend 2 Symmetrieoperationen. Insgesamt hat die Symmetriegruppe des Würfels 48 Elemente. Man bezeichnet sie in der Notation von Schoenflies als O_h, in der Notation von Hermann / Mauguin als $4/m\ \bar{3}\ 2/m$ oder allgemein aber etwas ungenau als Oktaeder- bzw. Würfelgruppe.

Beziehungen zu anderen Polyedern

Der Würfel ist das zum Oktaeder duale Polyeder (und umgekehrt). Außerdem beschreiben die Eckpunkte des Würfels zwei punktsymmetrische reguläre Tetraeder, welche zusammen das Sterntetraeder als weiteren regulären Körper bilden.

Mithilfe von Würfel und Oktaeder können zahlreiche Körper konstruiert werden, die ebenfalls die Würfelgruppe als Symmetriegruppe haben. So erhält man zum Beispiel

• den Hexaederstumpf bzw. den abgestumpften Würfel mit 6 Achtecken und 8 Dreiecken
• das Kuboktaeder mit 6 Quadraten und 8 Dreiecken, also 14 Seiten, und 12 Ecken
• den Oktaederstumpf bzw. das abgestumpfte Oktaeder mit 6 Quadraten und 8 Sechsecken

als Durchschnitte eines Würfels mit einem Oktaeder (siehe archimedische Körper) und

• das Rhombendodekaeder mit 6 + 8 = 14 Ecken und 12 Rhomben als Seiten

als konvexe Hülle einer Vereinigung eines Würfels mit einem Oktaeder.

Der Würfel ist Baustein der regulären Würfelparkettierung.

Formeln

Größen eines Würfels mit Kantenlänge a
Volumen	V = a3
Oberflächeninhalt	$O = 6 \, a^2 = V\,'(\rho)$
Umkugelradius	$R = \frac{a}{2} \sqrt{3}$
Kantenkugelradius	$r = \frac{a}{2} \sqrt{2}$
Inkugelradius	$\rho = \frac{a}{2}$
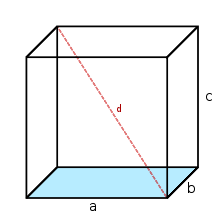
Raumdiagonale	$d = a \sqrt{3} = 2R$
Verhältnis von Volumen  zu Umkugelvolumen	$\frac{V}{V_{UK}} = \frac{2}{3\pi} \sqrt{3}$
Flächenwinkel  = 90°	$\cos \, \alpha = 0$
Flächen-Kanten-Winkel  = 90°	$\cos \, \beta = 0$

Verallgemeinerung

Auch die Analoga des Würfels in beliebiger Dimension n werden als (n-dimensionale) Würfel (oder Hyperwürfel) bezeichnet und sind ebenfalls reguläre Polytope. Der n-dimensionale Würfel hat $2^{n-k} \tbinom{n}{k}$ begrenzende Seiten der Dimension k. Spezialfälle:

• Der nulldimensionale Würfel (Punkt) hat 1 Ecke.
• Der eindimensionale Würfel (Strecke) hat 2 Ecken und 1 Kante.
• Der zweidimensionale Würfel (Quadrat) hat 4 Ecken, 4 Kanten und 1 Fläche
• Der vierdimensionale Hyperwürfel (Tesserakt) hat 16 Ecken, 32 Kanten, 24 Seitenquadrate und 8 Seitenwürfel.
• Der n-dimensionale Würfel hat 2ⁿ Ecken (k=0), n 2^{n − 1} Kanten (k=1), (n² − n) 2^{n − 3} Flächen (k=2), $n(\tfrac {n^2+2}{3}-n) \cdot 2^{n-4}$ Volumen (k=3) und 2n (n–1)-dimensionale Würfel als (k=n–1)-dimensionale Seiten (Facetten).

Ein Modell für den n-dimensionalen Würfel ist der Einheitswürfel Iⁿ im Vektorraum Rⁿ. Und zwar ist der abgeschlossene Einheitswürfel

• $I^n = \left\{ (x_1,\dots,x_n) \mid 0 \le x_i \le 1 \right\}$
• $I^n = [0,1] \times \cdots \times [0,1]$, das n-fache kartesische Produkt des Einheitsintervalls
• die konvexe Hülle der 2ⁿ Eckpunkte mit den Koordinaten 0 und 1
• der Durchschnitt der 2n Halbräume $x_i \ge 0$ und $x_i \le 1$

Der Einheitswürfel ist ein achsenparalleler Würfel mit der Kantenlänge 1 und einer Ecke im Koordinatenursprung. Eine Verallgemeinerung dieses Konzepts sind Quader im Rⁿ, die in der mehrdimensionalen Analysis eine Rolle spielen.

Siehe auch

• Würfelnetz
• Würfelverdoppelung

Weblinks

 Commons: Würfel – Sammlung von Bildern, Videos und Audiodateien

• Darstellung von Schrägbildern, Zentralprojektionen, Netzen und Schnitten von Würfeln
• Rätsel zur räumlichen Vorstellung von Würfeln
• interaktive Darstellung von mehrdimensionalen Würfeln

Platonische Körper

Tetraeder · Würfel · Oktaeder · Dodekaeder · Ikosaeder