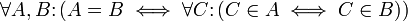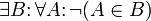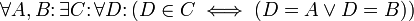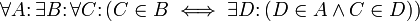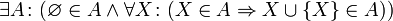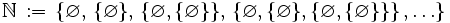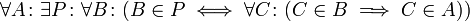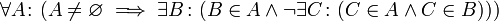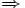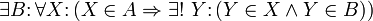- Zermelo Fraenkel
-
Die Zermelo-Fraenkel-Mengenlehre ist eine verbreitete axiomatische Mengenlehre, die nach Ernst Zermelo und Abraham Adolf Fraenkel benannt ist. Sie ist heute Grundlage fast aller Zweige der Mathematik. Die Zermelo-Fraenkel-Mengenlehre ohne Auswahlaxiom wird durch ZF abgekürzt, mit Auswahlaxiom durch ZFC (C = Choice (engl.)).
Inhaltsverzeichnis
Geschichte
Die Zermelo-Fraenkel-Mengenlehre ist eine Erweiterung der Zermelo-Mengenlehre von 1907. 1921 ergänzte Fraenkel das Ersetzungsaxiom. 1930 fügte Zermelo selbst noch das Fundierungsaxiom hinzu und komplettierte damit das Axiomensystem der Zermelo-Fraenkel-Mengenlehre, die er selbst als ZF-System bezeichnete. Das originale ZF-System ist verbal und kalkuliert auch Urelemente ein, die keine Mengen sind. Auf solche Urelemente verzichten spätere formalisierte ZF-Systeme (mit stärkerem Extensionalitätsaxiom); sie stellen daher eine „reine“ Mengenlehre dar, deren Objekte ausschließlich Mengen sind. Die erste präzise prädikatenlogische Formalisierung der reinen ZF-Mengenlehre schuf Thoralf Skolem 1929 noch ohne Fundierungsaxiom.
Die Axiome von ZF und ZFC
ZF hat unendlich viele Axiome, da zwei Axiomenschemata (8. und 9.) verwendet werden, die zu jedem Prädikat mit bestimmten Eigenschaften je ein Axiom angeben. Als logische Grundlage dient die Prädikatenlogik der ersten Stufe mit Identität und dem undefinierten Elementprädikat
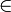 .
.1. Extensionalitätsaxiom oder Axiom der Bestimmtheit: Zwei Mengen sind genau dann gleich, wenn sie dieselben Elemente enthalten.
2. Leermengenaxiom oder Nullmengenaxiom: Es gibt eine Menge ohne Elemente.
-
- Aus dem Extensionalitätsaxiom folgt unmittelbar die Eindeutigkeit dieser Menge B, das heißt, dass es auch nicht mehr als eine solche Menge gibt. Diese wird meist als
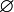 geschrieben und leere Menge genannt. Das bedeutet: Die leere Menge ist in ZF das einzige Urelement. Andere Urelemente sind nur beim allgemeineren originalen Axiom der Bestimmtheit von Zermelo möglich.
geschrieben und leere Menge genannt. Das bedeutet: Die leere Menge ist in ZF das einzige Urelement. Andere Urelemente sind nur beim allgemeineren originalen Axiom der Bestimmtheit von Zermelo möglich.
3. Paarmengenaxiom: Für alle A und B gibt es eine Menge C, die genau A und B als Elemente hat.
-
- Offenbar ist auch diese Menge C eindeutig bestimmt. Sie wird geschrieben als {A,B}. Die Menge {A,A} wird üblicherweise als {A} geschrieben.
4. Vereinigungsaxiom: Für jede Menge A gibt es eine Menge B, deren Elemente genau die Elemente der Elemente von A sind.
-
- Auch die Menge B ist eindeutig bestimmt und heißt die Vereinigung der Elemente von A, geschrieben als
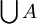 . Zusammen mit dem Paarmengenaxiom lässt sich die Vereinigung
. Zusammen mit dem Paarmengenaxiom lässt sich die Vereinigung 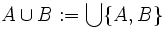 definieren.
definieren.
5. Unendlichkeitsaxiom: Es gibt eine Menge A, die die leere Menge und mit jedem Element x auch die Menge
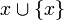 enthält (vgl. Induktive Menge).
enthält (vgl. Induktive Menge).-
- Es gibt viele derartige Mengen. Der Schnitt aller dieser Mengen ist die kleinste Menge mit diesen Eigenschaften und bildet die Menge der natürlichen Zahlen; die Bildung der Schnittmenge erfolgt durch Anwendung des Aussonderungsaxioms (s.u.). Die natürlichen Zahlen werden also dargestellt durch
6. Potenzmengenaxiom: Für jede Menge A gibt es eine Menge P, deren Elemente genau die Teilmengen von A sind.
-
- Die Menge P ist eindeutig bestimmt. Sie heißt die Potenzmenge von A und wird mit
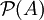 bezeichnet.
bezeichnet.
7. Fundierungsaxiom oder Regularitätsaxiom: Jede nichtleere Menge A enthält ein Element B, so dass A und B disjunkt sind.
-
- Das Element B, welches zu A disjunkt ist, ist im allgemeinen nicht eindeutig bestimmt.
- Das Fundierungsaxiom verhindert, dass es unendliche oder zyklische Folgen von Mengen gibt, bei denen jeweils eine in der nächsten enthalten ist,
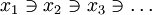 , denn dann könnte man eine Menge
, denn dann könnte man eine Menge 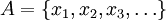 bilden, die dem Axiom widerspricht: Für jedes
bilden, die dem Axiom widerspricht: Für jedes 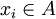 ist
ist 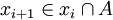 , die beiden Mengen sind also nicht disjunkt.
, die beiden Mengen sind also nicht disjunkt.
- Das Fundierungsaxiom verhindert, dass es unendliche oder zyklische Folgen von Mengen gibt, bei denen jeweils eine in der nächsten enthalten ist,
8. Aussonderungsaxiom: Hier handelt es sich um ein Axiomenschema mit je einem Axiom zu jedem einstelligen Prädikat P: Zu jeder Menge A existiert eine Teilmenge von A, die genau die Elemente C von A enthält, für die P(C) wahr ist.
-
- Für jedes einstellige Prädikat P gilt:
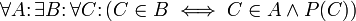
- Für jedes einstellige Prädikat P gilt:
- Aus dem Extensionalitätsaxiom ergibt sich sofort, dass es genau eine solche Menge gibt. Diese wird mit
 notiert.
notiert.
9. Ersetzungsaxiom (Fraenkel): Hier handelt es sich um ein Axiomenschema mit je einem Axiom für jedes zweistellige Prädikat F, das eine Abbildung repräsentiert, so dass aus F(X,Y) und F(X,Z) stets Y=Z folgt. Das einzige Y, für das F(X,Y) gilt, wird dann gewöhnlich als Y=F(X) geschrieben. Das Ersetzungsaxiom besagt dann: Für jede Menge A gibt es eine Menge B, deren Elemente genau die Bilder der Menge A unter der Abbildung F sind.
-
- Für jede Abbildung F gilt:

- Für jede Abbildung F gilt:
- Die Menge B ist durch F und die „Definitionsmenge“ A eindeutig bestimmt und wird mit
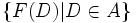 bezeichnet.
bezeichnet.
In der Mathematik wird häufig auch das Auswahlaxiom benutzt, das ZF zu ZFC erweitert:
10. Auswahlaxiom: Ist A eine Menge von paarweise disjunkten nichtleeren Mengen, dann gibt es eine Menge, die genau ein Element aus jedem Element von A enthält.
-
- Eine andere übliche verbale Formulierung des Auswahlaxioms lautet: Ist A eine Menge nichtleerer Mengen, dann gibt es eine Funktion f (von A in seine Vereinigung), die jedem Element B von A ein Element von B zuordnet („ein Element von B auswählt“).
- Mit den ZF-Axiomen kann man die Äquivalenz des Auswahlaxioms mit dem Wohlordnungssatz und dem Lemma von Zorn ableiten.
Vereinfachtes ZF-System (Redundanz)
Das ZF-Axiomensystem ist redundant, das heißt, es hat überflüssige Axiome, die aus anderen ableitbar sind. Die Zermelo-Fraenkel-Mengenlehre ZF wird schon durch die Axiome 1, 4–7 und 9 vollständig beschrieben, aufgrund folgender Punkte:
- Das Leermengenaxiom folgt aus dem Unendlichkeitsaxiom per Aussonderung (Fraenkel).
- Das Paarmengenaxiom folgt aus dem Ersetzungsaxiom, dem Leermengenaxiom und dem Potenzmengenaxiom (Zermelo).
- Das Aussonderungsaxiom ist mit dem Ersetzungsaxiom beweisbar (Zermelo). Das Ersetzungsaxiom ist ein verallgemeinertes Aussonderungsaxiom.
ZF-System ohne Gleichheit
Man kann ZF auch auf einer Prädikatenlogik ohne Identität aufbauen, indem man eine Definition der Gleichheit vornimmt:[1]
-
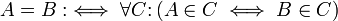 .
.
Diese Definition darf nicht mit dem Extensionalitätsaxiom verwechselt werden, denn sie besagt, dass Elemente gleich sind, wenn sie in denselben Mengen liegen. Man kann mit ihr und der Extensionalität alle üblichen Gleichheitsaxiome beweisen, so dass Gleichungen aus dem ZF-Axiomensystem eliminierbar sind.
Literatur
Primärquellen (chronologisch)
- Zermelo, Ernst: Untersuchungen über die Grundlagen der Mengenlehre, 1907, in: Mathematische Annalen 65 (1908) S. 261-281
- Fraenkel, Adolf Abraham: Zu den Grundlagen der Cantor-Zermeloschen Mengenlehre, 1921, in: Mathematische Annalen 86 (1922) S. 230-237
- Skolem, Thoralf: Über einige Grundlagenfragen der Mathematik, 1929, in: selected works in logic, Oslo, 1970, S. 227-273
- Zermelo, Ernst: Über Grenzzahlen und Mengenbereiche, in: Fundamenta Mathematicae 16 (1930), S. 29-47
Sekundärliteratur
- Deiser, Oliver: Einführung in die Mengenlehre : Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo. Springer, Berlin/Heidelberg 2004, ISBN 3-540-20401-6
- Ebbinghaus, Heinz-Dieter: Einführung in die Mengenlehre. Spektrum Akademischer Verlag, Heidelberg-Berlin 2003, ISBN 3-8274-1411-3.
- Fraenkel, Adolf: Einleitung in die Mengenlehre. Springer Verlag, Berlin-Heidelberg-New York 1928. Neudruck: Dr. Martin Sändig oHG, Walluf 1972, ISBN 3-500-24960-4.
- Halmos, Paul R.: Naive Mengenlehre. Vandenhoeck & Ruprecht, Göttingen 1968, ISBN 3-525-40527-8.
- Hausdorff, Felix: Grundzüge der Mengenlehre. Chelsea Publ. Co., New York 1914,1949,1965.
- Oberschelp, Arnold: Allgemeine Mengenlehre, Mannheim, Leipzig, Wien, Zürich, 1994
Einzelbelege
- ↑ eine gleichwertige Definition enthält: Walter Felscher: Naive Mengen und abstrakte Zahlen I, Mannheim, Wien, Zürich, 1978, S.78f
Weblinks
- Laura Crosilla: „Set Theory: Constructive and Intuitionistic ZF“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- mathematik.de: Mengenlehre
-
Wikimedia Foundation.