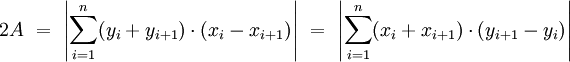- Zwölfeck
-
Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei voneinander verschiedene Punkte in einer Zeichenebene durch Strecken miteinander verbindet, sodass durch den entstandenen Linienzug eine zusammenhängende Fläche (Figur) umschlossen wird. Auch diese so entstandene Fläche wird oft Polygon genannt. Dreiecke, Vierecke und Sechsecke sind aus dem Alltag bekannte Beispiele für Polygone.
Inhaltsverzeichnis
Mathematische Definition
Ein Polygon ist eine Figur, die durch ein Tupel
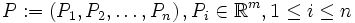 von n Punkten (die Eckpunkte oder kurz Ecken genannt werden) eindeutig definiert wird.
von n Punkten (die Eckpunkte oder kurz Ecken genannt werden) eindeutig definiert wird.Die Strecken
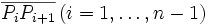 und
und 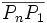 bezeichnet man als Seiten oder Kanten des Polygons, alle anderen Verbindungsstrecken
bezeichnet man als Seiten oder Kanten des Polygons, alle anderen Verbindungsstrecken 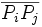 zweier Polygon-Eckpunkte als Diagonalen.
zweier Polygon-Eckpunkte als Diagonalen.Meist werden noch weitere Bedingungen vorausgesetzt:
- Das Polygon hat mindestens drei paarweise voneinander verschiedene Eckpunkte.
- Drei angrenzende Eckpunkte liegen nicht auf einer Geraden. Auch Pn,P1,P2 und Pn − 1,Pn,P1 gelten als angrenzende Eckpunkte.
Mathematische Beziehungen
Innenwinkel
In einem nicht überschlagenen, ebenen n-Eck ist die Summe der Innenwinkel
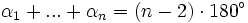 .
.
Sind darüber hinaus alle Innenwinkel gleich groß, so haben diese den Wert
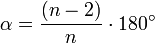 .
.
Anzahl der Diagonalen
Für konvexe Polygone gilt zur Berechnung der Anzahl der Diagonalen folgende Überlegung:
- Jede der n Ecken kann durch eine Strecke mit einer der anderen Ecken verbunden werden.
- Die Verbindung von Ecke Pa zur Ecke Pb ist mit der Verbindung von Pb nach Pa identisch.
- Genau n Verbindungen sind Seiten des Polygons.
Also hat ein konvexes n-Eck genau
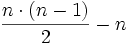 Diagonalen.
Diagonalen.Fläche
Wenn die Eckpunkte eines ebenen einfachen (s.o.) Polygons durch kartesische Koordinaten (xi,yi) gegeben sind, kann man die Fläche des Polygons nach der Gaußschen Trapezformel berechnen:
Wobei die Indizes, die größer als n sind, immer modulo n betrachtet werden müssen, d.h. mit xn + 1 ist x1 gemeint.
Besondere Polygone
Unter den beliebig vielen möglichen Polygonen stellen die nachstehend aufgelisteten Klassen von Polygonen etwas Besonderes dar. Einige von ihnen können entweder unerwarteterweise exakt (Beispiel 65537-Eck) oder in sehr guter Näherung (Beispiel Siebeneck) mit Zirkel und Lineal konstruiert werden. Andere haben neben der geometrischen eine Bedeutung als Form in der Architektur (Beispiel Pentagon) oder in der Symbolik (Beispiel Pentagramm).
- Dreieck (Triangel)
- Viereck (Tetragon)
- Fünfeck (Pentagon)
- Sechseck (Hexagon)
- Siebeneck (Heptagon)
- Achteck (Oktogon)
- Neuneck (Nonagon, Enneagon)
- Siebzehneck (Heptadekagon)
- 257-Eck
- 65537-Eck
Spezielle Typen
Regelmäßige Polygone
einfaches, nicht überschlagenes, planares, konvexes, regelmäßiges Siebeneck
Vielecke können gleichseitig oder gleichwinklig sein. Hat ein Vieleck gleiche Seiten und gleiche Innenwinkel, dann wird es als reguläres oder regelmäßiges Vieleck bezeichnet. Reguläre Vielecke sind isogonal.
Ein reguläres n-Eck hat stets einen Umkreis mit Radius ru und einen Inkreis mit Radius ri. Die Länge jeder Seite wird mit a bezeichnet, die Seitenanzahl mit n. Daraus ergeben sich folgende Formeln für reguläre, nicht-überschlagene Polygone:
- Flächeninhalt
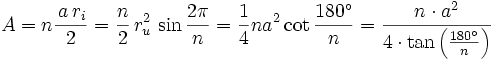
- Inkreisradius
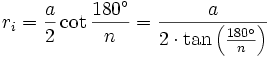
- Umkreisradius
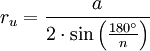
Ein regelmäßiges oder reguläres Polygon ist ein Vieleck, dessen Ecken gleichabständig, also unter gleichem Zentriwinkel, auf einem Kreis liegen.
- Wichtige Kenndaten: (r = Radius des Umkreises)
Regelmäßige Polygone Polygon Seitenlänge
aZentriwinkel
αUmfang
uFläche
ADreieck 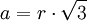
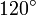
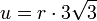
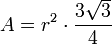
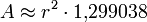
Quadrat 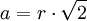
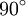
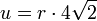
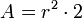
Fünfeck 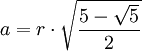
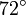
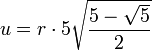
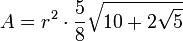
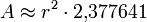
Sechseck 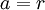
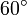
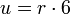
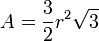
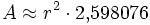
Siebeneck 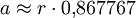
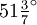
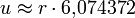
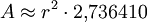
Achteck 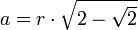
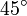
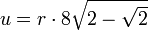
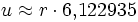
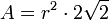
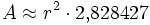
Neuneck 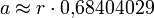
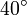
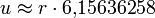
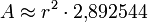
Zehneck 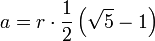
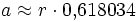
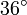
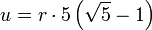
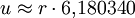
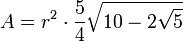
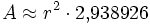
Zwölfeck 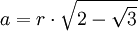
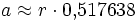
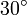
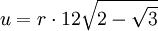
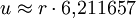
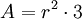
n-Eck 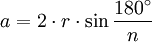
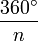
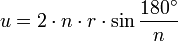
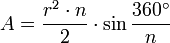
Grenzwert 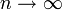 (Kreis)
(Kreis)
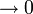
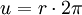
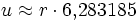
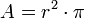
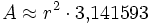
andere Typen
- Schneiden (berühren) sich die Kanten nicht nur in den Eckpunkten, bezeichnet man das Polygon als überschlagen.
- Falls der Schnitt zweier Kanten entweder leer oder eine Ecke ist, und jede Ecke zu höchstens zwei Kanten gehört (das heißt, es liegt keine Selbstüberschneidung vor), bezeichnet man das Polygon als einfach.
- Nicht überschlagene Vielecke können konvex (alle Innenwinkel sind kleiner als 180°) oder nichtkonvex (mindestens ein Innenwinkel ist größer als 180°) sein.
- Man unterscheidet in der Ebene liegende (planare) und im Raum liegende (nicht-planare) Polygone.
- Planare überschlagene reguläre Polygone werden wegen ihres Aussehens auch als Sternpolygone bezeichnet.
Berühmte Vielecke
- das „Pentagon“ (Sitz des US-Verteidigungsministeriums);
- das Pentagon in Kronach: die Festung Rosenberg zeigt ein Fünfeck als Grundriss;
- Frankreich wird aufgrund seiner geographischen Form auch als Hexagon bezeichnet;
- das karolingische Oktogon im Grundriss des Aachener Doms;
- Castel del Monte in Apulien als Oktogon im Grundriss.
Polygone in der Computergraphik
In der 3D-Computergrafik werden beliebige (auch gekrümmte) Oberflächen als Polygonnetz modelliert. Insbesondere Dreiecksnetze eignen sich besonders gut zur schnellen Darstellung von Oberflächen.
Zur Speicherung von polygonalen Netzen gibt es eine Reihe bekannter Datenstrukturen.
Siehe auch
- Polyeder, Polytop, Winkelsumme, Außenwinkel
- Satz von Pick (für Polygone auf dem Gitter)
- Häufigkeitspolygon
- konstruierbare Polygone
- Graham Scan
Weblinks
Wikimedia Foundation.