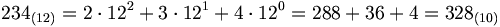Zwölfersystem

Das Duodezimalsystem (auch Zwölfersystem) ist ein Stellenwertsystem zur Darstellung von Zahlen. Es verwendet die Basis Zwölf, ist also das „12-adische Stellenwertsystem“. Das bedeutet: Anders als beim üblichen Dezimalsystem (mit der Basis 10) gibt es 12 Ziffern, so dass erst für natürliche Zahlen ab 12 eine zweite Ziffer benötigt wird.

Verwendung und Geschichte

Die Zahl 12 hatte in vielen Kulturen eine wichtige Bedeutung. Sie gilt als die Zahl der Vollkommenheit. Ein Grund sind vermutlich die 12 Mond-Monate im Jahr. Beispiele der Verwendung der 12 sind die 12 Monate im Jahr, zweimal 12 Stunden pro Tag, 12 Tierkreiszeichen, 12 Zeichen in der chinesischen Astrologie, 12 Sterne auf der Flagge der Europäischen Union (nicht von den Gründungsstaaten abgeleitet). In vielen europäischen Sprachen gibt es eigene Zahlennamen für 11 („elf“) und 12 („zwölf“) anstelle der regelmäßigen Zehnersystem-Namen (wie „zweiundzehn“ oder „zweizehn“). Dies weist, wie auch die Verwendung des Dutzends, auf eine breite Verwendung der Basis 12 hin.

Zusätzlich hat die 12 die Eigenschaft, durch relativ viele Zahlen ganzzahlig teilbar zu sein (1, 2, 3, 4, 6, 12), was die Verwendung als Größeneinteilung (z. B. bei Zoll und Fuß) zur Folge hatte.

Ein kleiner Nachteil gegenüber dem Hexadezimalsystem, den das Duodezimal- mit dem Dezimal- und dem Oktalsystem teilt, ist, dass die Quadratwurzel der Basis keine ganze Zahl ist.

Das Duodezimalsystem wird heute noch in einigen Zusammenhängen verwendet:

• 1 Dutzend = 12 Stück, 1 Schock = 5 Dutzend, 1 Gros = 12 Dutzend, 1 Maß = 12 Gros
• bei verschiedenen Maßeinheiten, z. B. 1 Fuß = 12 Zoll,
• Einteilung des Tages in 2 mal 12 Stunden.

Ansätze, das Dezimalsystem mit zwei zusätzlichen Ziffern zu ergänzen, um allgemein im Duodezimalsystem zu rechnen, konnten sich dagegen nicht durchsetzen.

Ein- und zweihändiges Zählen mit Fingergliedern und Fingern^[1]

Im gewohnten Dezimalsystem (10er-System) zählt man mit den 10 Fingern (2 mal 5) beider Hände. In einigen Gegenden der Welt existierte aber ein Zählen mit Hilfe der Fingerglieder, das einhändig zur Zahl zwölf, zweihändig aber zur Zahl 60 führt.

Einhändiges Zählen bis 12

Gezählt wird mit dem Daumen als Zeiger und den Fingergliedern der gleichen Hand als Zählobjekt.

• Das einhändige Zählen z. B. einer Herde Tiere beginnt, indem man für das erste Tier mit dem Daumen der rechten Hand die Spitze, also das oberste Fingerglied, des kleinen Fingers der gleichen Hand, also der rechten Hand, berührt.
• Das zweite Objekt der zu zählenden Menge zählt man, indem man für die Zahl zwei mit dem Daumen der rechten Hand das mittlere Fingerglied des kleinen Fingers der rechten Hand berührt.
• Das dritte Objekt zählt man, indem man mit dem Daumen nunmehr das untere Fingerglied des kleinen Fingers berührt.
• Nun steht kein weiteres Fingerglieder am kleinen Finger mehr zur Verfügung. Deshalb zählt man das vierte Objekt nunmehr, indem man mit dem Daumen das oberste Fingerglied des Ringfingers berührt.
• Für das fünfte Objekt berührt man mit dem Daumen nun das mittlere Glied des Ringfingers.
• Das sechste Objekt zählt man, indem nunmehr das unterste Fingerglied des Ringfingers berührt.
• Da nun auch der Ringfinger erschöpft ist, zählt man die sieben, in dem man mit dem Daumen das oberste Fingerglied des Mittelfingers berührt.
• Die Acht zählt man nunmehr in dem man das mittlere Fingerglied des Mittelfingers berührt.
• Die Neun zählt man, indem man das unterste Fingerglied des Mittelfingers berührt.
• Die Zehn zählt man, indem man das oberste Fingerglied des Zeigefingers berührt.
• Die Elf zählt man, indem man das mittlere Fingerglied des Zeigefingers mit dem Daumen berührt.
• Die Zwölf zählt man, indem man das unterste Fingerglied des Zeigefingers mit dem Daumen berührt.

In diesem Fingerzählsystem ist also in der ersten Runde der Daumen der Zeiger und nicht der Zeigefinger, wie wir es gewohnt sind. Die Tatsache, dass im Deutschen alle Zahlen bis zwölf eigene Namen haben,

• danach aber die Wörter Zahlen mit zusammengesetzten Zahlennamen (dreizehn, vierzehn …) und
• abgeleiteten Zahlennamen (zwanzig aus zwei, dreißig aus drei, achtzig aus acht, einhundert, eintausend, …) gebildet werden, könnte die Vermutung begründen, dass dieses Zählsystem auch von früheren Sprechern des Deutschen angewandt wurde.

Zählt man so mit der Basis Zwölf kann man leicht auf den Gedanken kommen den ganzen Tag, wie es die Babylonier taten, oder den hellen Tag, wie es die Ägypter taten, in 12 Stunden einzuteilen.

Das Duodezimalzählsystem an einer Hand ist bezeugt in Indien, Indochina, Pakistan, Afghanistan, im Iran, in der Türkei, im Irak und in Ägypten.

Zweihändiges Zählen bis 60

Nachdem mit Hilfe des Daumens als Zeiger mit den jeweils drei Fingergliedern der restlichen vier Finger der gleichen Hand, drei mal vier Fingerglieder das erste Dutzend, z. B. Tiere, abgezählt ist, ist die Zählkapazität der rechten Hand zunächst erschöpft.

• Die linke Hand ist zur Faust geballt. Um sich zu merken, dass ein Dutzend gezählt wurde, streckt man nun einen Finger, z. B. den Daumen aus.
• Nun zählt man die Zahl dreizehn, in dem man wieder mit der rechten Hand weiterzählt, also mit dem Daumen der rechten Hand das oberste Fingerglied des kleinen Fingers berührt.
• Und so zählt man, wen nötig, das zweite Dutzend voll.
• Umfasst die zu zählende Herde mehr als das zweite Dutzend so streckt man, nachdem man mit der rechten Hand das zweite Dutzend gezählt hat, den zweiten Finger der linken Hand aus, z. B. nach dem Daumen den Zeigefinger.
• Dann beginnt man erneut, das dritte Dutzend mit den Fingergliedern der rechten Hand zu zählen.
• Mit den fünf Fingern der linken Hand kann man so fünf mal ein Dutzend abzählen, also 5 mal 12 gleich sechzig (60).
• Nun kann man noch einmal mit der rechten Hand das nächste Dutzend zählen, also mit zwei Händen bis zu z. B. 72 Tiere zählen (5 × 12 an der linken Hand und 12 an der rechten Hand). Damit sind zwei Hände aber erschöpft.
• Bei größeren Zahlen wäre es aber besser, sich nunmehr mit einem Stock oder einem Stein oder einen anderen Hilfsmittel die erste volle linke Hand, die ersten fünf mal zwölf, also sechzig zu merken.

Dieses Fingerzählsystem existiert noch in Teilen der Türkei, des Irak, in Indien und Indochina.

Vierhändiges Zählen bis 600

• Statt Stöcken oder Steinen konnte man beim Zählen einer großen Herde auf die zwei mal fünf, also zehn Finger eines zweiten Menschen, z. B. eines zweiten Hirten zurückgreifen.
• Hat der erste Hirte an seiner linke Hand die fünf Dutzend, also sechzig, voll gezählt, so streckt der zweite Hirte, der bisher seine zwei Hände zur Faust geballt hat, an der ersten Hand einen Finger aus.
• Sind die zweiten 60 beim zählenden ersten Hirten gezählt, streckt der zweite Hirte den zweiten Finger aus.
• Das machen die beiden so weiter, bis die zehn Finger des zweiten Hirten für 10 mal 60, also 600 gezählte Tiere, voll sind.
• Genau so gut, kann natürlich der zweite Hirte alle Finger zunächst strecken und dann für jedes volle 60 einen Finger krümmen.

Sumerer

• Bei den Sumerern trug die 60 den Namen Gesch.
• 120: gesch-min (60 × 2)
• 180: gesch-esch (60 × 3)
• 240: gesch-limmu (60 × 4)
• 300: gesch-iá (60 × 5)
• 360: gesch-asch (60 × 6)
• 420: gesch-imin (60 × 7)
• 480: gesch-ussu (60 × 8)
• 540: gesch-ilummu (60 × 9)
• 600: gesch-u (60 × 10)
• Nun zählten die Sumerer nicht in 60er-Schritten (gesch-Schritten) weiter, sondern im 600 (gesch-u-Schritten) und zwar sechs mal 600, also bis 3.600, das schàr genannt wurde.
• Die 3.600 wurden dann wieder zehn mal gesteigert bis schàr-u (3.600 × 10) 36.000.
• Die 36.000 wurden sechs mal gezählt bis 216.000 schàr-gal, wörtlich das große 3.600 (also 60 × 60 × 60).
• Die 216.000 wurde zehn mal gezählt bis 2.160.000 schàr-gal-u (=(60 × 60 × 60) x 10)
• Da schàr-gal-u wurde zunächst fünf mal vervielfacht. Die sechste Vielfache 12.960.000, also 60 × *60 × 60 × 60) erhielt wieder einen eigenen Namen schàr-gal-shu-nu-tag (dem großen schàr übergeordnete Einheit)

Darstellung von Zahlen

Ziffern

Die Dozenal Society of America (gegr. 1944) schlug zusätzlich zu den Ziffern 0 bis 9 noch X für 10 und E für 11 vor, später dann # für 10. Die Zahl 278 würde dann z. B. als 1E2 (1 · 144 + 11 · 12 + 2 · 1) geschrieben. Die Nachteile davon liegen auf der Hand – weitere gängige Bedeutungen der Zeichenfolge 1E2 sind nämlich

• die Abkürzung der Exponentialschreibweise 1 * 10^2 und
• die Hexadezimalzahl 0x1E2 = 1 * 256 + 14 * 16 + 2.

Die Dozenal Society of Great Britain (gegr. 1959) bevorzugt stattdessen die um 180 Grad gedrehten Ziffern 2 und 3.

In diesem Artikel verwenden wir die Ziffern # und E für Zehn und Elf.

Ganze und rationale Zahlen

Die Darstellung der Zahlen erfolgt ähnlich wie die Darstellung im gewöhnlich verwendeten Dezimalsystem, mit dem Unterschied, dass die Wertigkeit der Ziffern nicht durch die entsprechende Zehnerpotenz, sondern durch die passende Zwölferpotenz bestimmt wird. Beispielsweise stellt die Ziffernfolge 234 nicht (wie im Dezimalsystem) die Zweihundertvierunddreißig dar, sondern die Dreihundertachtundzwanzig, denn im Duodezimalsystem berechnet sich der Wert durch:

$234_{(12)} = 2\cdot 12^2 + 3\cdot 12^1 + 4\cdot 12^0 = 288+36+4=328_{(10)}$

Die Indices weisen dabei auf die verwendete Basis hin.

Duodezimale Brüche sind wie im Dezimalsystem entweder endlich, wie

1/2 = 0,6₍₁₂₎

1/3 = 0,4₍₁₂₎

1/6 = 0,2₍₁₂₎

1/8 = 0,16₍₁₂₎

1/9 = 0,14₍₁₂₎

oder periodisch, wie

1/5 = 0,2497 2497 2497 …₍₁₂₎

1/7 = 0,186#35 186#35 …₍₁₂₎

1/10 = 1/#₍₁₂₎ = 0,1 2497 2497 …₍₁₂₎

Negative Zahlen schreibt man wie im Dezimalsystem mit einem vorangestellte Minuszeichen.

Grundrechenarten

Ganz analog zu den Zahlen im Dezimalsystem lassen sich mit Duodezimalzahlen die gängigen arithmetischen Grundoperation Addition, Subtraktion, Multiplikation und Division durchführen. Die benötigten Algorithmen sind prinzipiell dieselben, nur werden durch die größere Anzahl von Ziffern das kleine Einmaleins und die Additionstabelle größer.

Umrechnen in andere Stellenwertsysteme

Die ersten natürlichen Zahlen werden im Duodezimalsystem so dargestellt:

Duodezimalsystem	0	1	2	3	4	5	6	7	8	9	#	E	10	11	12	13	14	15	16	17	18	19	1#	1E	20
Dezimalsystem	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24

Vom Duodezimalsystem ins Dezimalsystem

Um aus einer Duodezimalzahl eine Dezimalzahl zu erhalten, zählt man die angegebenen Vielfachen der 12er-Potenzen zusammen, berechnet also den Wert der Zahl wie es die Definition des 12-adischen Stellenwertsystems vorgibt:

234₍₁₂₎ = 2 · 12² + 3 · 12¹ + 4 · 12⁰ = 288 + 36 + 4 = 328.

Vom Dezimalsystem ins Duodezimalsystem

Eine Möglichkeit, eine Dezimalzahl ins Duodezimalsystem umzuwandeln, ist die Betrachtung der Divisionsreste die entstehen, wenn die Zahl durch die Basis 12 geteilt wird.

Im Beispiel der 328₍₁₀₎ sähe das so aus:

328: 12 = 27 Rest 4,
 27: 12 = 2 Rest 3,
  2: 12 = 0 Rest 2.

Der zu erreichende Wert ist nun von unten nach oben an den Resten ablesbar: 234₍₁₂₎.

Einzelnachweis

1. ↑ Georges Ifrah: Universalgeschichte der Zahlen, 1993, Campus Verlag GmbH, Frankfurt, Lizenzausgabe Zweitausendund eins, Frankfurt, ISBN 978-3-86150-704-8, Seiten 69–75 u. 90–92

Weblinks

• Dozenal Society of America
• Dozenal Society of Great Britain