- Χ-Quadrat-Verteilung
-
Die Chi-Quadrat-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen.
Im Allgemeinen ist mit „Chi-Quadrat-Verteilung“ die zentrale Chi-Quadrat-Verteilung gemeint. Ihr einziger Parameter n kann, muss aber nicht, eine natürliche Zahl sein und heißt ihre Zahl der Freiheitsgrade.
Die Chi-Quadrat-Verteilung berechnet die Wahrscheinlichkeit des Auftretens bestimmter Werte der Summe unabhängiger quadrierter standardnormalverteilter Zufallsvariablen, wie sie beispielsweise in der Ermittlung der Varianz einer Stichprobe auftreten können. Sie findet außerdem Anwendung beim Chi-Quadrat-Test.
Inhaltsverzeichnis
Definition
Die Chi-Quadrat-Verteilung mit n Freiheitsgraden ist die Verteilung der Summe
n unabhängiger quadrierter standardnormalverteilter Zufallsvariablen, d. h.
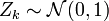 für
für 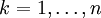 .
.
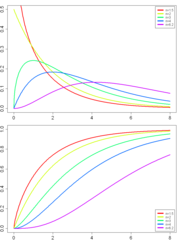
Dichte
Die Dichte fn der
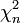 -Verteilung mit n Freiheitsgraden hat die Form:
-Verteilung mit n Freiheitsgraden hat die Form:Dabei steht Γ(r) für die Gammafunktion. Die Werte von
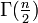 kann man auch berechnen mit
kann man auch berechnen mit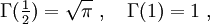
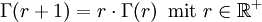 .
.
Verteilungsfunktion
Die Verteilungsfunktion kann man nicht in elementarer Form schreiben, jedoch mit Hilfe der regularisierten unvollständigen Gammafunktion:
Sie beschreibt die Wahrscheinlichkeit, dass
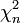 im Intervall [0, x] liegt.
im Intervall [0, x] liegt.Beispiel
Man macht n Messungen einer Grösse x, die aus einer normalverteilten Grundgesamtheit stammt. Sei
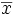 der Mittelwert der n gemessenen Werte und
der Mittelwert der n gemessenen Werte unddie Summe der quadrierten Abweichungen vom Mittelwert. Dann lässt sich z.B. das 95%-Konfidenzintervall für die Varianz σ2 angeben:
wobei
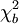 durch
durch 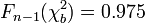 und
und 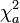 durch
durch 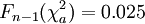 bestimmt wird. Die Grenzen ergeben sich daraus, dass
bestimmt wird. Die Grenzen ergeben sich daraus, dass 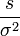 wie
wie 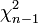 verteilt ist.
verteilt ist.Eigenschaften
Erwartungswert
Der Erwartungswert der Chi-Quadrat-Verteilung ist
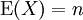 .
.
Unter der Voraussetzung einer standardnormalverteilten Grundgesamtheit sollte also bei richtiger Abschätzung der Varianz der Grundgesamtheit der Wert
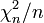 in der Nähe von 1 liegen.
in der Nähe von 1 liegen.Varianz
Die Varianz der Chi-Quadrat-Verteilung ist
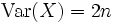 .
.
Modus
Der Modus der Chi-Quadrat-Verteilung ist n − 2 für
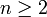 .
.Schiefe
Die Schiefe der Chi-Quadrat-Verteilung ist
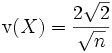 .
.
Charakteristische Funktion
Die charakteristische Funktion für
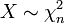 hat die Form
hat die FormSumme χ2-verteilter Zufallsvariablen
Sind X1,X2,...,Xn unabhängige Zufallsvariable, mit
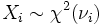 , so gilt:
, so gilt:Die Chi-Quadrat-Verteilung ist also reproduktiv.
Nichtzentrale Chi-Quadrat-Verteilung
Wenn die normalverteilten Zufallsvariablen nicht bezüglich ihres Erwartungswertes μi(i = 1,...,n) zentriert sind (d.h. wenn nicht alle μi = 0 sind), erhält man die nichtzentrale Chi-Quadrat-Verteilung. Sie hat als zweiten Parameter neben n den Nichtzentralitätsparameter λ > 0.
Seien
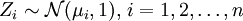 , so ist
, so ist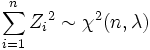 mit
mit 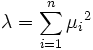 .
.
Insbesondere folgt aus
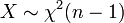 und
und 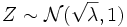 , dass
, dass 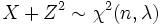 ist.
ist.Eine zweite Möglichkeit, eine nichtzentrale Chi-Quadrat-Verteilung zu erzeugen, ist als Mischverteilung der zentralen Chi-Quadrat-Verteilung. Dabei ist
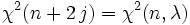 ,
,
wenn
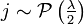 aus einer Poisson-Verteilung gezogen wird.
aus einer Poisson-Verteilung gezogen wird.Die Dichtefunktion der nichtzentralen Chi-Quadrat-Verteilung ist
![f(x)=\frac{\exp{\left[-\frac{1}{2}(x+\lambda)\right]}}{2^{\frac{n}{2}}}\,
\sum_{j=0}^\infty \frac{x^{\frac{n}{2}+j-1}\lambda^j}{2^{2j}\,\Gamma\left(\frac{n}{2}+j\right)\,j!}](/pictures/dewiki/48/088cdc2b1b1d0b9be49aa2202fabe2e9.png) für
für 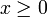 , f(x) = 0 für x < 0.
, f(x) = 0 für x < 0.
Darstellung durch modifizierte Bessel-Funktion
Die Dichtefunktion kann alternativ auch mit Hilfe der modifizierten Bessel-Funktion erster Gattung Iq(x) dargestellt werden:
![f(x)=\frac{\exp{\left[-\frac{1}{2}(x+\lambda)\right]} x^{\frac{1}{2}(n-1)} \sqrt{\lambda}}{2(\lambda x)^{\frac{n}{4}}}\,
I_{\frac{n}{2}-1}\left(\sqrt{\lambda x}\right)](/pictures/dewiki/102/f35e6cd1f68af5086bb30219c69a29e5.png) für
für 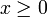 .
.
Beziehung zu anderen Verteilungen
Beziehung zur Gammaverteilung
Die Chi-Quadrat-Verteilung ist ein Spezialfall der Gammaverteilung. Ist
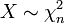 , so gilt
, so giltBeziehung zur Normalverteilung
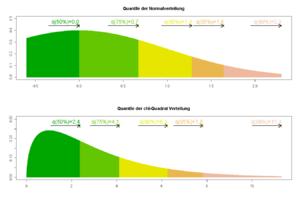 Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung
Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung- Die Summe
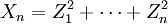 von n unabhängigen quadrierten standardnormalverteilten Zufallsvariablen
von n unabhängigen quadrierten standardnormalverteilten Zufallsvariablen 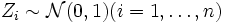 genügt einer Chi-Quadrat-Verteilung
genügt einer Chi-Quadrat-Verteilung 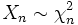 mit n Freiheitsgraden.
mit n Freiheitsgraden.
- Für
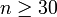 ist
ist 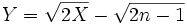 näherungsweise standardnormalverteilt.
näherungsweise standardnormalverteilt.
- Für n > 100 ist die Zufallsvariable X näherungsweise normalverteilt, mit Erwartungswert n und Standardabweichung
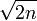 .
.
Beziehung zur Exponentialverteilung
Eine Chi-Quadrat-Verteilung mit 2 Freiheitsgraden ist eine Exponentialverteilung
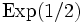 mit dem Parameter λ = 1 / 2.
mit dem Parameter λ = 1 / 2.Beziehung zur Erlang-Verteilung
Eine Chi-Quadrat-Verteilung mit 2n Freiheitsgraden ist identisch mit einer Erlang-Verteilung mit n Freiheitsgraden und λ = 1 / 2.
Beziehung zur F-Verteilung
Wenn
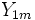 und
und 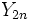 unabhängige
unabhängige 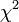 -verteilte Zufallsvariablen mit den Freiheitsgraden m und n sind, dann ist der Quotient
-verteilte Zufallsvariablen mit den Freiheitsgraden m und n sind, dann ist der Quotienteine Zufallsvariable, die der F-Verteilung mit den Freiheitsgraden (m,n) genügt.
Beziehung zur stetigen Gleichverteilung
Für gerade n = 2m kann man die
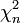 -Verteilung als m-fache Faltung bilden mit Hilfe der gleichmäßig stetige Dichte U(0,1):
-Verteilung als m-fache Faltung bilden mit Hilfe der gleichmäßig stetige Dichte U(0,1):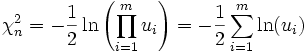 ,
,
worin die ui m unabhängige gleichmäßig stetig verteilten Zufallsvariablen sind.
Für ungerade n gilt dagegen
Literatur
Hartung, Joachim / Elpelt, Bärbel / Klösener, Karl-Heinz: Statistik, 12. Auflage, Oldenbourg 1999, S. 152 ff., ISBN 3486249843.
Weblinks
- uni-konstanz – Interaktive Animation
- Webrechner für Werte der Chi-Quadrat-Verteilung
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.


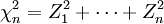
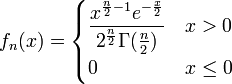
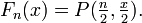
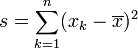
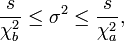
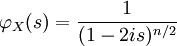
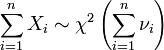
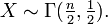
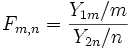
![\chi_n^2 = \chi_{n-1}^2 + \left[\mathcal{N}(0,1)\right]^{2}](/pictures/dewiki/102/fbd68e0816b5ee52faf8654f5d6e97f4.png)