- Chi-Quadrat-Verteilung
-
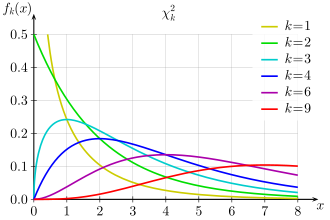
Die Chi-Quadrat-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Im Allgemeinen ist mit „Chi-Quadrat-Verteilung“ die zentrale Chi-Quadrat-Verteilung gemeint. Ihr einziger Parameter n muss eine natürliche Zahl sein und heißt ihre Zahl der Freiheitsgrade.
Sie ist eine der Verteilungen, die aus der Normalverteilung abgeleitet wird. Hat man n Zufallsvariablen Zi, die unabhängig und standard normalverteilt sind, so ist die Chi-Quadrat-Verteilung mit n Freiheitsgraden definiert als die Verteilung der Summe der quadrierten Zufallsvariablen
 . Solche Summen quadrierter Zufallsvariablen treten bei der Schätzung der Varianz einer Stichprobe auf. Die Chi-Quadrat-Verteilung findet außerdem Anwendung bei den Chi-Quadrat-Tests.
. Solche Summen quadrierter Zufallsvariablen treten bei der Schätzung der Varianz einer Stichprobe auf. Die Chi-Quadrat-Verteilung findet außerdem Anwendung bei den Chi-Quadrat-Tests.Sie wurde 1875 eingeführt von Friedrich Robert Helmert, die Bezeichnung stammt von Karl Pearson (1900).[1]
Inhaltsverzeichnis
Definition
Die Chi-Quadrat-Verteilung mit n Freiheitsgraden beschreibt die Verteilung der Summe n stochastisch unabhängiger quadrierter standardnormalverteilter Zufallsvariablen
 , mit
, mit  für
für  .
.
Das Zeichen
 ist Kurzschreibweise für ' ist verteilt wie '. Die Summe quadrierter Größen kann keine negativen Werte annehmen.
ist Kurzschreibweise für ' ist verteilt wie '. Die Summe quadrierter Größen kann keine negativen Werte annehmen.Dichte
Die Dichte fn der
 -Verteilung mit n Freiheitsgraden hat die Form:
-Verteilung mit n Freiheitsgraden hat die Form:Dabei steht Γ(r) für die Gammafunktion. Die Werte von
 kann man auch berechnen mit
kann man auch berechnen mit
 .
.
Verteilungsfunktion
Die Verteilungsfunktion kann man mit Hilfe der regularisierten unvollständigen Gammafunktion schreiben:
Wenn n eine natürliche Zahl ist, dann kann die Verteilungsfunktion (mehr oder weniger) elementar dargestellt werden:
wobei Erf die Fehlerfunktion bezeichnet. Die Verteilungsfunktion beschreibt die Wahrscheinlichkeit, dass
 im Intervall [0, x] liegt.
im Intervall [0, x] liegt.Eigenschaften
Erwartungswert
Der Erwartungswert der Chi-Quadrat-Verteilung mit n Freiheitsgraden ist
 .
.
Unter der Voraussetzung einer standardnormalverteilten Grundgesamtheit sollte also bei richtiger Abschätzung der Varianz der Grundgesamtheit der Wert
 in der Nähe von 1 liegen.
in der Nähe von 1 liegen.Varianz
Die Varianz der Chi-Quadrat-Verteilung mit n Freiheitsgraden ist
 .
.
Modus
Der Modus der Chi-Quadrat-Verteilung mit n Freiheitsgraden ist n − 2 für
 .
.Schiefe
Die Schiefe v der Chi-Quadrat-Verteilung mit n Freiheitsgraden ist
 .
.
Die Chi-Quadrat-Verteilung besitzt eine positive Schiefe, d.h. sie ist linkssteil bzw. rechtsschief. Je höher die Anzahl der Freiheitsgrade n, desto weniger schief ist die Verteilung.
Kurtosis
Die Kurtosis (Wölbung) β2 der Chi-Quadrat-Verteilung mit n Freiheitsgraden ist gegeben durch
 .
.Der Exzess γ2 gegenüber der Normalverteilung ergibt sich damit zu
 .[2] Daher gilt: Je höher die Anzahl der Freiheitsgrade n, desto geringer der Exzess.
.[2] Daher gilt: Je höher die Anzahl der Freiheitsgrade n, desto geringer der Exzess.Charakteristische Funktion
Die charakteristische Funktion für
 hat die Form
hat die Form .
.
Summe χ2-verteilter Zufallsvariablen
Sind
 unabhängige Zufallsvariable, mit
unabhängige Zufallsvariable, mit  , so gilt:
, so gilt: .
.
Die Chi-Quadrat-Verteilung ist also reproduktiv.
Nichtzentrale Chi-Quadrat-Verteilung
Wenn die normalverteilten Zufallsvariablen nicht bezüglich ihres Erwartungswertes
 zentriert sind (d.h. wenn nicht alle μi = 0 sind), erhält man die nichtzentrale Chi-Quadrat-Verteilung. Sie hat als zweiten Parameter neben n den Nichtzentralitätsparameter λ > 0.
zentriert sind (d.h. wenn nicht alle μi = 0 sind), erhält man die nichtzentrale Chi-Quadrat-Verteilung. Sie hat als zweiten Parameter neben n den Nichtzentralitätsparameter λ > 0.Seien
 , so ist
, so ist mit
mit  .
.
Insbesondere folgt aus
 und
und  , dass
, dass  ist.
ist.Eine zweite Möglichkeit, eine nichtzentrale Chi-Quadrat-Verteilung zu erzeugen, ist als Mischverteilung der zentralen Chi-Quadrat-Verteilung. Dabei ist
 ,
,
wenn
 aus einer Poisson-Verteilung gezogen wird.
aus einer Poisson-Verteilung gezogen wird.Dichtefunktion
Die Dichtefunktion der nichtzentralen Chi-Quadrat-Verteilung ist
![f(x)=\frac{\exp{\left[-\frac{1}{2}(x+\lambda)\right]}}{2^{\frac{n}{2}}}\,
\sum_{j=0}^\infty \frac{x^{\frac{n}{2}+j-1}\lambda^j}{2^{2j}\,\Gamma\left(\frac{n}{2}+j\right)\,j!}](8/088cdc2b1b1d0b9be49aa2202fabe2e9.png) für
für  ,
,  für
für  .
.
Darstellung durch modifizierte Bessel-Funktion
Die Dichtefunktion kann alternativ auch mit Hilfe der modifizierten Bessel-Funktion erster Gattung Iq(x) dargestellt werden:
![f(x)=\frac{\exp{\left[-\frac{1}{2}(x+\lambda)\right]} x^{\frac{1}{2}(n-1)} \sqrt{\lambda}}{2(\lambda x)^{\frac{n}{4}}}\,
I_{\frac{n}{2}-1}\left(\sqrt{\lambda x}\right)](7/a7739fe5ee402d204c6abe54babc3285.png) für
für  .
.
Verteilungsfunktion
Die Verteilungsfunktion der nichtzentralen Chi-Quadrat-Verteilung kann mit Hilfe der Marcum-Q-Funktion QM(a,b) dargestellt werden. [3]
Beispiel
Man macht n Messungen einer Größe x, die aus einer normalverteilten Grundgesamtheit stammen. Sei
 der Mittelwert der n gemessenen Werte und
der Mittelwert der n gemessenen Werte unddie Stichprobenvarianz. Dann lässt sich z. B. das 95%-Konfidenzintervall für die Varianz σ2 angeben:
wobei
 durch
durch  und
und  durch
durch  bestimmt wird, und deshalb auch
bestimmt wird, und deshalb auch  . Die Grenzen ergeben sich daraus, dass
. Die Grenzen ergeben sich daraus, dass  wie
wie  verteilt ist.
verteilt ist.Herleitung der Verteilung der Stichprobenvarianz
Sei
 eine Stichprobe von n Messwerten, gezogen aus einer normalverteilten Zufallsvariablen X mit arithmetischem Mittelwert
eine Stichprobe von n Messwerten, gezogen aus einer normalverteilten Zufallsvariablen X mit arithmetischem Mittelwert  und Stichprobenvarianz
und Stichprobenvarianz  als Schätzfunktionen für Mittelwert μ und Varianz σ2 der Grundgesamtheit.
als Schätzfunktionen für Mittelwert μ und Varianz σ2 der Grundgesamtheit.Dann lässt sich zeigen, dass
 verteilt ist wie
verteilt ist wie  .
.Dazu werden nach Helmert[4] die (xi) mittels einer orthonormalen Linearkombination in neue Variablen (yj) transformiert. Die Transformation lautet:
Die neuen unabhängigen Variablen yi sind wie X normalverteilt mit gleicher Varianz
 , aber mit Erwartungswert
, aber mit Erwartungswert  beides aufgrund der Faltungsinvarianz der Normalverteilung.
beides aufgrund der Faltungsinvarianz der Normalverteilung.Außerdem gilt für die Koeffizienten aij in
 wegen der Orthonormalität
wegen der Orthonormalität  (Kronecker-Delta) und damit
(Kronecker-Delta) und damit 
Deshalb ergibt sich nun
und schlussendlich nach Division durch σ2
Der Ausdruck auf der linken Seite ist offenbar verteilt wie eine Summe von quadrierten standardnormalverteilten unabhängigen Variablen mit n − 1 Summanden, wie für
 gefordert.
gefordert.Demnach ist also
 , während laut Definition der Chi-Quadrat-Summe
, während laut Definition der Chi-Quadrat-Summe  . Ein Freiheitsgrad wird hier 'verbraucht', denn der berechnete Mittelwert
. Ein Freiheitsgrad wird hier 'verbraucht', denn der berechnete Mittelwert  ist im Gegensatz zum Mittelwert der Grundgesamtheit μ von den
ist im Gegensatz zum Mittelwert der Grundgesamtheit μ von den  abhängig.
abhängig.Beziehung zu anderen Verteilungen
Beziehung zur Gammaverteilung
Die Chi-Quadrat-Verteilung ist ein Spezialfall der Gammaverteilung. Ist
 , so gilt
, so giltBeziehung zur Normalverteilung
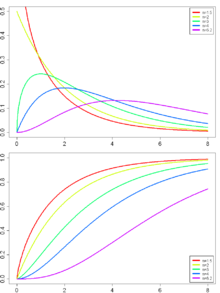
 Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung
Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung
- Die Summe
 von n unabhängigen quadrierten standardnormalverteilten Zufallsvariablen
von n unabhängigen quadrierten standardnormalverteilten Zufallsvariablen  genügt einer Chi-Quadrat-Verteilung
genügt einer Chi-Quadrat-Verteilung  mit n Freiheitsgraden.
mit n Freiheitsgraden.
- Für
 ist
ist  näherungsweise standardnormalverteilt.
näherungsweise standardnormalverteilt.
- Für n > 100 ist die Zufallsvariable X näherungsweise normalverteilt, mit Erwartungswert n und Standardabweichung
 bzw. bei einer nicht-zentralen Chi-Quadrat-Verteilung mit Erwartungswert n + λ und Standardabweichung
bzw. bei einer nicht-zentralen Chi-Quadrat-Verteilung mit Erwartungswert n + λ und Standardabweichung  .
.
Beziehung zur Exponentialverteilung
Eine Chi-Quadrat-Verteilung mit 2 Freiheitsgraden ist eine Exponentialverteilung
 mit dem Parameter
mit dem Parameter  .
.Beziehung zur Erlang-Verteilung
Eine Chi-Quadrat-Verteilung mit 2n Freiheitsgraden ist identisch mit einer Erlang-Verteilung
 mit n Freiheitsgraden und
mit n Freiheitsgraden und  .
.Beziehung zur F -Verteilung
Wenn
 und
und  unabhängige
unabhängige  -verteilte Zufallsvariablen mit den Freiheitsgraden m und n sind, dann ist der Quotient
-verteilte Zufallsvariablen mit den Freiheitsgraden m und n sind, dann ist der Quotienteine Zufallsvariable, die der F-Verteilung mit den Freiheitsgraden
 genügt.
genügt.Beziehung zur stetigen Gleichverteilung
Für gerade n = 2m kann man die
 -Verteilung als m-fache Faltung bilden mit Hilfe der gleichmäßig stetigen Dichte U(0,1):
-Verteilung als m-fache Faltung bilden mit Hilfe der gleichmäßig stetigen Dichte U(0,1): ,
,
worin die ui m unabhängige gleichmäßig stetig verteilte Zufallsvariablen sind.
Für ungerade n gilt dagegen
Herleitung der Dichtefunktion
Die Dichte der Zufallsvariable
 , mit
, mit  unabhängig und standardnormalverteilt, ergibt sich aus der gemeinsamen Dichte der Zufallsvariablen
unabhängig und standardnormalverteilt, ergibt sich aus der gemeinsamen Dichte der Zufallsvariablen  . Diese gemeinsame Dichte ist das n-fache Produkt der Standardnormalverteilungsdichte:
. Diese gemeinsame Dichte ist das n-fache Produkt der Standardnormalverteilungsdichte:Für die gesuchte Dichte gilt:
mit

Im Grenzwert ist die Summe im Argument der Exponentialfunktion gleich z, sie darf deshalb vor das Integral und den Limes gezogen werden.
Das verbleibende Integral
entspricht dem Volumen der Schale zwischen der Kugel mit Radius
 und der Kugel mit Radius
und der Kugel mit Radius  ,
,wobei
 das Volumen der n-dimensionalen Kugel mit Radius R angibt.
das Volumen der n-dimensionalen Kugel mit Radius R angibt.Es folgt:

und nach Einsetzen in den Ausdruck für die gesuchte Dichte:
 .
.
Quantilfunktion
Die Quantilfunktion der χ2-Verteilung xp ist die Lösung der Gleichung
 und damit prinzipiell über die Umkehrfunktion zu berechnen. Konkret gilt hier
und damit prinzipiell über die Umkehrfunktion zu berechnen. Konkret gilt hiermit P − 1 als Inverse der regularisierten unvollständigen Gammafunktion. Dieser Wert xp ist in der Quantiltabelle unter den Koordinaten p und n eingetragen.
Für wenige Werte n (1, 2, 4) kann man die Quantilfunktion explizit angeben:
wobei
 die Fehlerfunktion,
die Fehlerfunktion,  den unteren Zweig der Lambertschen W-Funktion bezeichnet und e die Eulersche Zahl.
den unteren Zweig der Lambertschen W-Funktion bezeichnet und e die Eulersche Zahl.Literatur
- Joachim Hartung, Bärbel Elpelt, Karl-Heinz Klösener: Statistik. 12. Auflage. Oldenbourg, 1999, ISBN 3-486-24984-3, S. 152 ff.
Einzelnachweise
- ↑ F. R. Helmert. In: Zeitschrift fuer Math. und Physik 21, 1875, S. 102-219. Karl Pearson: On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it Can Reasonably Be Supposed to have Arisen from Random Sampling. In: Philosophical Magazine 5, Band 50, 1900, S. 157-175. Zitiert nach L. Schmetterer: Mathematische Statistik. Springer, Wien 1966, S. 93
- ↑ Wolfram Mathworld
- ↑ Albert H. Nuttall: Some Integrals Involving the QM Function. In: IEEE Transactions on Information Theory. Nr. 21, 1975, ISSN 0018-9448, S. 95–96 (IEEE Xplore).
- ↑ Helmert, Astronomische Nachrichten 88, 1876, S.113-132
Weblinks
- uni-konstanz – Interaktive Animation
- Webrechner für Werte der Chi-Quadrat-Verteilung
-
 Wikibooks: Tabelle der χ2-Verteilung – Lern- und Lehrmaterialien
Wikibooks: Tabelle der χ2-Verteilung – Lern- und Lehrmaterialien
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Chi-Quadrat-Verteilung — [çiː ], χ2 Verteilung, ältere Bezeichnung Hẹlmert Pearson Verteilung [ pɪəsn , nach K. Pearson], Stochastik: die 1876 von F. R. Helmert angegebene Verteilung χn2 mit n Freiheitsgraden, definiert als die Verteilung der Summe der Quadrate von n… … Universal-Lexikon
Chi-Quadrat-Verteilung — stetige theoretische ⇡ Verteilung, die durch Helmert (1876) und Pearson (1900) als Prüfverteilung eingeführt wurde. Sind n ⇡ Zufallsvariablen Xi (i = 1, ..., n) stochastisch unabhängig und jeweils standardnormalverteilt (⇡… … Lexikon der Economics
Chi-Quadrat — (χ2) ist eine Testgröße, mittels der ein Signifikanztest (auch: statistischer Test), der Chi Quadrat Test, durchgeführt wird. Der Chi Quadrat Test basiert auf dem Vergleich zwischen erwarteten und beobachteten Werten zweier Merkmale in einer… … Deutsch Wikipedia
Chi-Quadrat-Statistik — Chi Quadrat (χ2) ist eine Testgröße, mittels der ein Signifikanztest (auch: statistischer Test), der Chi Quadrat Test, durchgeführt wird. Der Chi Quadrat Test basiert auf dem Vergleich zwischen erwarteten und beobachteten Werten zweier Merkmale… … Deutsch Wikipedia
Chi Quadrat — (χ2) ist eine Testgröße, mittels der ein Signifikanztest (auch: statistischer Test), der Chi Quadrat Test, durchgeführt wird. Der Chi Quadrat Test basiert auf dem Vergleich zwischen erwarteten und beobachteten Werten zweier Merkmale in einer… … Deutsch Wikipedia
Chi-Quadrat-Test — Mit Chi Quadrat Test (χ² Test) bezeichnet man in der mathematischen Statistik eine Gruppe von Hypothesentests mit χ² verteilter Testprüfgröße. Man unterscheidet vor allem die folgenden Tests: Verteilungstest oder Anpassungstest: Hier wird geprüft … Deutsch Wikipedia
Chi-Quadrat-Anpassungstest — Mit dem χ2 Test (Chi Quadrat Test) untersucht man Verteilungseigenschaften einer statistischen Grundgesamtheit. Man unterscheidet vor allem die beiden Tests: Verteilungstest oder Anpassungstest: Hier wird geprüft, ob vorliegende Daten auf eine… … Deutsch Wikipedia
Chi Quadrat Test — Mit dem χ2 Test (Chi Quadrat Test) untersucht man Verteilungseigenschaften einer statistischen Grundgesamtheit. Man unterscheidet vor allem die beiden Tests: Verteilungstest oder Anpassungstest: Hier wird geprüft, ob vorliegende Daten auf eine… … Deutsch Wikipedia
Chi-Quadrat-Test — ⇡ statistisches Testverfahren; zentrale Anwendung: Prüfung einer Hypothese über die Verteilung eines Merkmals (Anpassungstest), z.B. Prüfung einer Hypothese über die ⇡ Anteilswerte pi (i = 1, ..., k) der Kategorien eines ⇡ qualitativen… … Lexikon der Economics
Chi-Quadrat-Test — Chi Quadrat Test, ein häufig angewandtes statistisches Verfahren (Statistik), mit dessen Hilfe z. B. Häufigkeitsunterschiede bei mehrklassigen qualitativen Merkmalen auf Signifikanz geprüft werden können. Mit dem Chi Quadrat Test lässt sich… … Universal-Lexikon

















![\chi_n^2 = \chi_{n-1}^2 + \left[\mathcal{N}(0,1)\right]^{2}](1/7517e0386bccec47dd488dc55ff3ad90.png)






