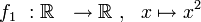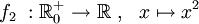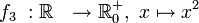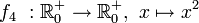Bijektive Abbildung

Eine bijektive Funktion.

Bijektivität (bijektiv oder umkehrbar eindeutig auf oder eineindeutig auf) ist eine Eigenschaft einer mathematischen Funktion.

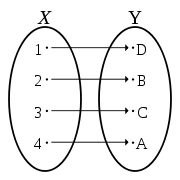
Eine Funktion ist bijektiv, wenn sie verschiedene Elemente ihres Definitionsbereichs auf verschiedene Elemente der Zielmenge abbildet (sie also injektiv ist), und wenn zusätzlich jedes Element der Zielmenge als Funktionswert auftritt (sie also surjektiv ist). Eine bijektive Funktion hat daher immer eine Umkehrfunktion, ist also invertierbar.

Eine bijektive Funktion nennt man auch eine Bijektion. Eine Bijektion einer endlichen Menge auf sich selbst heißt auch Permutation.

Für endliche Mengen haben die Definitionsmenge, die Bildmenge und die Zielmenge einer Bijektion dieselbe Anzahl von Elementen. Umgekehrt ist eine Funktion zwischen endlichen Mengen bijektiv, wenn diese drei Zahlen übereinstimmen.

Für unendliche Mengen definiert man die Mächtigkeit als Verallgemeinerung der Elementanzahl mit Hilfe des Begriffes der Bijektion.

Definition

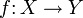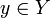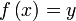Sei f eine Funktion, die von X nach Y abbildet, also $f \colon X \to Y$. f ist bijektiv, wenn für alle $y \in Y$ genau ein $x \in X$ mit $f\left(x\right) = y$ existiert.

Mit anderen Worten kann man dies so ausdrücken: f ist bijektiv, wenn f injektiv und surjektiv ist.

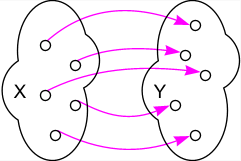
Grafische Veranschaulichungen

Das Prinzip der Bijektivität: Jeder Punkt in der Zielmenge (Y) wird genau einmal getroffen.

Vier bijektive streng monoton steigende reelle Funktionen.

Vier bijektive streng monoton fallende reelle Funktionen.

Beispiele und Gegenbeispiele

Die Menge der reellen Zahlen wird hier mit $\mathbb{R}$ bezeichnet, die Menge der nichtnegativen reellen Zahlen mit $\R^+_0$.

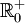• Die Funktion 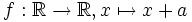$f: \R\to\R, x\mapsto x+a$ ist bijektiv mit der Umkehrfunktion $f^{-1}: \R\to\R, x\mapsto x-a$.
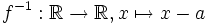• Ebenso ist für 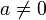$a\ne 0$ die Funktion 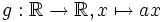$g: \R\to\R, x\mapsto ax$ bijektiv mit der Umkehrfunktion $g^{-1}: \R\to\R, x\mapsto \frac{x}{a}$.
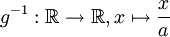• Unmathematisches Beispiel: Ordnet man jedem (monogam) verheirateten Menschen seinen Ehepartner bzw. seine Ehepartnerin zu, ist dies eine Bijektion der Menge aller verheirateten Menschen auf sich selbst. Dies ist sogar ein Beispiel für eine selbstinverse Abbildung.

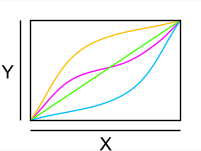
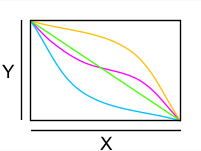
• Die folgenden vier Quadratfunktionen unterscheiden sich nur in ihren Definitions- bzw. Wertemengen:

$f_1\ :\mathbb{R}\ \ \rightarrow\mathbb{R}\ , \ \ x \mapsto x^2$

$f_2\ : \R^+_0\rightarrow\mathbb{R}\ , \ \ x \mapsto x^2$

$f_3\ : \mathbb{R}\ \ \rightarrow \R^+_0,\ x \mapsto x^2$

$f_4\ : \R^+_0\rightarrow \R^+_0,\ x \mapsto x^2$

Mit diesen Definitionen ist

f₁ nicht injektiv, nicht surjektiv, nicht bijektiv

f₂ injektiv, nicht surjektiv, nicht bijektiv

f₃ nicht injektiv, surjektiv, nicht bijektiv

f₄ injektiv, surjektiv, bijektiv

Eigenschaften

• Sind A und B endliche Mengen mit gleich vielen Elementen und ist 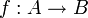$f : A \to B$ eine Funktion, dann gilt:
  Ist f injektiv, dann ist f bereits bijektiv.
  Ist f surjektiv, dann ist f bereits bijektiv.

• Insbesondere gilt also für Funktionen 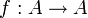$f : A \to A$ von einer endlichen Menge A in sich selbst:
  f ist injektiv ⇔ f ist surjektiv ⇔ f ist bijektiv.
  Für unendliche Mengen ist das im Allgemeinen falsch. Diese können injektiv auf echte Teilmengen abgebildet werden, ebenso gibt es surjektive Abbildungen einer unendlichen Menge auf sich selbst, die keine Bijektionen sind.
  Solche Überraschungen werden im Artikel Hilberts Hotel detaillierter beschrieben, siehe dazu auch Dedekind-Unendlichkeit.
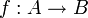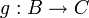• Sind die Funktionen $f : A \to B$ und $g : B \to C$ bijektiv, dann gilt dies auch für die Verkettung 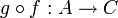$g\circ f : A \to C$. Die Umkehrfunktion von 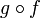$g\circ f$ ist dann $f^{-1}\circ g^{-1}$.

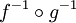• Ist 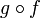$g\circ f$ bijektiv, dann ist f injektiv und g surjektiv.

• Ist 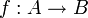$f : A \to B$ eine Funktion und gibt es eine Funktion 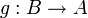$g : B \to A$, die die beiden Gleichungen
  $g \circ f = \operatorname{id}_A$ ($\operatorname{id}_A$ = Identität auf der Menge A)
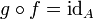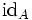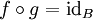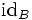  $f \circ g = \operatorname{id}_B$ ($\operatorname{id}_B$ = Identität auf der Menge B)
  erfüllt, dann ist f bijektiv, und g ist die Umkehrfunktion von f, also g = f ^{− 1}.
• Die Bijektionen einer Menge A in sich selbst bilden, zusammen mit der Verkettung als Verknüpfung, eine Gruppe, die, falls A endlich ist, „symmetrische Gruppe“ heißt.

Siehe auch

• Isomorphismus (eine strukturerhaltende Bijektion)

Literatur

Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.

Weblinks