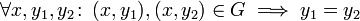- Abbildung (Mathematik)
-
In der Mathematik ist eine Funktion oder Abbildung eine Beziehung zwischen zwei Mengen, die jedem Element der einen Menge (Eingangsgröße, Funktionsargument, unabhängige Variable, x-Wert) ein Element der anderen Menge (Ausgangsgröße, Funktionswert, abhängige Variable, y-Wert) zuordnet. Das Konzept der Funktion oder Abbildung nimmt in der modernen Mathematik eine zentrale Stellung ein; es enthält als Spezialfälle unter anderem parametrische Kurven, Skalar- und Vektorfelder, Koordinatentransformationen, Operatoren und vieles mehr.
Begriffsgeschichte
Das Nebeneinander der Begriffe „Funktion“ und „Abbildung“ ist nur historisch zu verstehen.
Der Begriff „Funktion“, 1694 von Leibniz eingeführt, wurde zunächst als formelmäßige Rechenvorschrift aufgefasst, zum Beispiel y = x2 oder f(x) = sinx. In der Schulmathematik wurde dieser naive Funktionsbegriff bis weit in die zweite Hälfte des 20. Jahrhunderts beibehalten. Bisweilen wurden auch mehrdeutige Funktionen, zum Beispiel eine im Vorzeichen unbestimmte Quadratwurzelfunktion, zugelassen.
Erst als die Analysis im 19. Jahrhundert mit einem exakten Grenzwertbegriff auf eine neue Grundlage gestellt wurde, entdeckten Weierstraß, Dedekind und andere, dass Grenzwerte unendlicher Folgen „klassischer“ Funktionen sprunghaft sein können und sich nicht immer durch „geschlossene“ Formeln (mit endlich vielen Rechenoperationen) ausdrücken lassen. Das erzwang eine schrittweise Ausweitung des Funktionsbegriffs.
Davon unabhängig wurde im 19. Jahrhundert die Gruppentheorie begründet, mit der man systematisch untersuchen kann, wie sich algebraische Gleichungen unter der Wirkung aufeinanderfolgender Transformationen verändern. Bei der Anwendung dieser Theorie auf geometrische Probleme wurden gleichbedeutend mit „Transformation“ auch die Begriffe „Bewegung“ und „Abbildung“ gebraucht.
Als Anfang des 20. Jahrhunderts die Grundlagen der Mathematik einheitlich in der Sprache der Mengenlehre formuliert wurden, stellten sich die Begriffe „Funktion“ und „Abbildung“ dann als deckungsgleich heraus. Im Sprachgebrauch wirken die unterschiedlichen Traditionen jedoch fort. In der Analysis spricht man heute häufig noch von Funktionen, während man in der Algebra und in der Geometrie von Abbildungen spricht. Einige Mathematiker unterscheiden auch heute noch streng zwischen einer Abbildung und einer Funktion. Diese verstehen unter einer Funktion eine Abbildung in den reellen oder komplexen Zahlenkörper.
Weitere Synonyme in spezielleren Zusammenhängen sind unter anderem Operation in der Analysis, Verknüpfung und Morphismus in der Algebra.
Definitionen und Konventionen
Grundidee
Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y einer Zielmenge Z zu.
Schreibweise:
Anmerkungen:
- Die Umkehrung gilt nicht: Ein Element der Zielmenge muss (wenn überhaupt) nicht nur einem Element des Definitionsbereiches zugeordnet worden sein.
- Oft ist an Stelle der Definitionsmenge zunächst eine Quellmenge Q gegeben. Wenn f als Rechenvorschrift gegeben ist, erhält man die Definitionsmenge Df, indem man von Q diejenigen Elemente ausschließt, für die f nicht definiert ist.
Mengentheoretische Definition
Mengentheoretisch ist eine Funktion eine spezielle Relation:
- Eine Funktion von der Menge D in die Menge Z ist eine Menge f, die die folgenden Eigenschaften hat:
- f ist eine Teilmenge des kartesischen Produkts
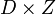 von D und Z, d. h. f eine Relation.
von D und Z, d. h. f eine Relation. - Für jedes Element x aus D existiert (mindestens) ein Element y in Z, so dass das geordnete Paar (x,y) Element der Relation f ist. f ist also linkstotal.
- Zu jedem Element x von D gibt es höchstens ein Element y von Z, so dass das Paar (x,y) in f liegt. f ist damit rechtseindeutig bzw. funktional.
- f ist eine Teilmenge des kartesischen Produkts
Die letzten beiden Eigenschaften lassen sich auch wie folgt zusammenfassen:
-
- Zu jedem Element x von D gibt es genau ein Element y von Z, so dass das Paar (x,y) Element der Relation f ist.
Oft möchte man aber auch die Zielmenge explizit zu einem Teil der Funktion machen, zum Beispiel um Aussagen zur Surjektivität anstellen zu können:
- Ein Paar f = (Gf,Z), bestehend aus einer Relation Gf und einer Menge Z, heißt Funktion von der Menge D nach Z, wenn gilt:
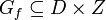 und zu jedem Element x von D gibt es genau ein Element y von Z (geschrieben y = f(x)), so dass das Paar (x,y) Element von Gf ist.
und zu jedem Element x von D gibt es genau ein Element y von Z (geschrieben y = f(x)), so dass das Paar (x,y) Element von Gf ist.
Gf wird auch der Graph der Funktion f genannt. Die Definitionsmenge D der Funktion ist dabei durch ihren Graphen eindeutig bestimmt und besteht aus den ersten Komponenten aller Elemente des Graphen. Stimmen zwei Funktionen in ihren Graphen überein, so sagt man auch, sie seien im Wesentlichen gleich.
Man kann jedoch auch noch die Definitionsmenge hinzunehmen und eine Funktion entsprechend als ein Tripel f = (Gf,D,Z), Gf wie oben, definieren.
Verschiedene Weisen, eine Funktion zu spezifizieren
Eine Zuordnung kann unter anderem in einer der folgenden Formen beschrieben werden:
- Funktionsterm
- x2
- Funktionsgleichung
- f(x) = x2
- Zuordnungsvorschrift
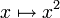
- Wertetabelle (für endliche, aber auch abzählbar unendliche Definitionsbereiche)
-
x 1 2 3 4 5 6 7 … y 1 4 9 16 25 36 49 …
- Als Relation insbesondere auch als aufgezählt oder beschrieben dargestellte Teilmenge
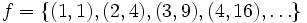
- Als Komposition von anderen Funktionen oder als Inverse einer anderen Funktion
Symbolische Schreibweisen
Für Funktionen gibt es etliche symbolische Schreibweisen, die jeweils einige spezielle Eigenschaften der Funktion ausdrücken. Im folgenden werden einige wichtige genannt.
-
Symbol Erklärung 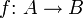
Funktion von A nach B 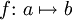
Funktion, die a auf b abbildet; statt b kann auch eine Formel o. Ä. stehen 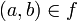
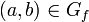
Funktion, die a auf b abbildet; statt b kann auch eine Formel o. Ä. stehen (mengentheoretische Schreibweise) 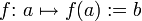
Funktion, die a auf b abbildet, die die elementweise Zuordnung mit Beschreibung der Funktionssymbolik (statt f(a) stehen oft Dinge wie 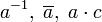 u. Ä.) und der Formel o. Ä. (an der Stelle von b) zur Berechnung des Bildes angibt
u. Ä.) und der Formel o. Ä. (an der Stelle von b) zur Berechnung des Bildes angibt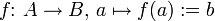
Ausführlichste Notation, die alle beteiligten Mengen und die elementweise Zuordnung mit Beschreibung der Funktionssymbolik und der Formel o. Ä. zur Berechnung des Bildes angibt 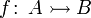
injektive Funktion von A nach B 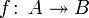
surjektive Funktion von A nach B 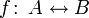
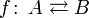
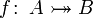
bijektive Funktion von A nach B 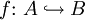
Inklusionsabbildung, natürliche Inklusion, natürliche Einbettung von A in B
(A ist Untermenge von B, und die Funktion bildet jedes Element von A auf sich ab.)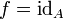
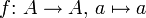
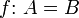
Identität, identische Abbildung auf A bzw. von A nach B
(A = B, und die Funktion bildet jedes Element auf sich ab.)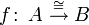
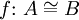
Isomorphismus von A nach B 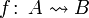
partielle Funktion (s. o.) von A nach B 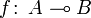
mehrdeutige Funktion (s. o.) von A nach B
Die Symbole können auch, wo sinnvoll, miteinander kombiniert werden.
Schreib- und Sprechweisen
Für die Zuordnung eines Funktionswertes y zu einem Argument x gibt es eine Reihe verschiedener Sprech- bzw. ausführlicher Schreibweisen, die alle mehr oder weniger gleichwertig sind und vor allem in Abhängigkeit von dem, was vordergründig ausgedrückt werden soll, vom jeweiligen Kontext, der benutzten Symbolik und auch vom Geschmack des Sprechers (Schreibers) gewählt werden. Hier einige Beispiele:
- „x wird abgebildet auf f von x“
- „f von x wird x zugeordnet“ (vornehmlich, wenn das
 -Symbol in der Symbolik steht)
-Symbol in der Symbolik steht) - „y gleich f von x“ (vornehmlich, wenn ein Gleichheitszeichen in der Symbolik steht)
- „y ist das Bild von x unter der Abbildung f“
Davon zu unterscheiden ist die Sprech- und Schreibweise: „y ist eine Funktion von x“, die vor allem in der Physik und in der Physik sehr nahe stehenden Bereichen der Mathematik auftaucht. Sie ist die ältere und ursprüngliche Sprech- und Schreibweise und beschreibt die Abhängigkeit einer Variablen y von einer anderen Variablen x, im Gegensatz dazu, dass mit Hilfe der Variablen x und y (stellvertretend) die Zuordnung bestimmter Elemente von Mengen beschrieben wird. Die „physikalische“ Sprechweise stammt von dem Vorgehen, erst zwei veränderlichen Größen (der physikalischen Realität) Symbole, nämlich die Variablen x und y, zuzuordnen, und danach deren Abhängigkeit festzustellen. Steht z. B. y für die Raumtemperatur und x für die Zeit, so wird man feststellen können, dass sich die Raumtemperatur in Abhängigkeit von der Zeit ändert und somit „die Raumtemperatur eine Funktion der Zeit ist“ bzw. stellvertretend „y eine Funktion von x ist.“
Statt Definitionsmenge A wird auch Definitionsbereich, Domain, Urbildmenge oder schlicht Urbild gesagt. Insbesondere im Falle partieller Funktionen wird zusätzlich von der Quellmenge gesprochen, diese heißt auch Quelle oder Source. Die Elemente von A heißen Funktionsargumente oder Urbilder, salopp auch x-Werte. Die Zielmenge B wird auch Wertemenge, Wertebereich, Codomain, Destination oder Target genannt, die Elemente von B heißen Zielwerte oder Zielelemente, salopp auch y-Werte. Funktionswerte, Bildelemente oder schlicht Bilder heißen dagegen nur diejenigen Elemente von B, die tatsächlich als Bild eines Arguments auftreten, die Menge der Funktionswerte heißt Bildmenge, Bild, Image oder Range von f.
Wertemenge/-bereich wird manchmal etwas uneinheitlich auch als Synonym zu Bildmenge benutzt.
Für die verschiedenen Mengen sind diverse Operatoren-Schreibweisen in Gebrauch, also Kurzschreibweisen, die einer Funktion f ihre verschiedenen Mengen zuordnen. Hier die gängigsten Beispiele:
-
Definitionsbereich 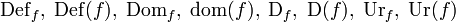
Quellmenge 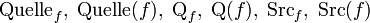
Bildmenge 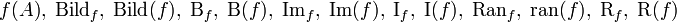
Wertebereich 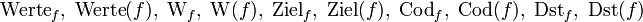
Insbesondere wird für jede Untermenge
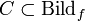 von
von 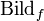 mit f − 1(C) das Urbild von C bezüglich der Funktion f bezeichnet. Es gilt dann
mit f − 1(C) das Urbild von C bezüglich der Funktion f bezeichnet. Es gilt dann 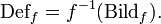 Dieses f − 1(C) ist nicht zu verwechseln mit dem Bild der Umkehrfunktion einer bijektiven Funktion, es ist nur eine Schreibweise für das Urbild; im Falle, dass f bijektiv ist, stimmen aber das so beschriebene Urbild von C bezüglich f und das Bild von C unter der Umkehrfunktion f − 1 überein.
Dieses f − 1(C) ist nicht zu verwechseln mit dem Bild der Umkehrfunktion einer bijektiven Funktion, es ist nur eine Schreibweise für das Urbild; im Falle, dass f bijektiv ist, stimmen aber das so beschriebene Urbild von C bezüglich f und das Bild von C unter der Umkehrfunktion f − 1 überein.Indizierung und Auswahlfunktion
Sind
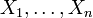 beliebige Mengen, so kann man das n-Tupel
beliebige Mengen, so kann man das n-Tupel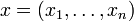 mit
mit 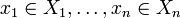
als Abbildung
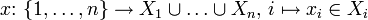 ,
,
auffassen. Man nennt x Auswahlfunktion.
Für n-Tupel sind andere Definition oftmals geläufiger, jedoch soll diese Definition helfen, den Begriff der Auswahlfunktion zu erweitern:
Man nennt eine Abbildung
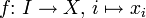 ,
,
auch eine Familie von Elementen aus X mit der Indexmenge I und schreibt sie
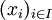 mit
mit 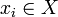 für alle
für alle 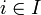 .
.Auch bei Matrizen gibt es eine Auswahlfunktion, dies wollen wir anhand eines Beispiels erläutern:
Sei die Matrix
gegeben. Nun ist eine Auswahlfunktion x gegeben durch
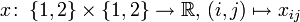 ,
,
wobei xij das Element der Matrix bezeichnet, das in der i-ten Zeile in der j-ten Spalte steht. Hier zum Beispiel der Wert 6 in Zeile 2, Spalte 1:
-
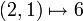 .
.
Falls die Indexmenge I überabzählbar ist, so ist die Existenz einer Auswahlfunktion x nicht selbstverständlich. Zur Sicherstellung dieser Existenz muss das Auswahlaxiom herangezogen werden.
Darstellung von Funktionen
Eine Funktion
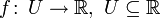 , kann man visualisieren, indem man ihren Graphen in ein (zweidimensionales) Koordinatensystem zeichnet. Der Funktionsgraph einer Funktion f kann mathematisch definiert werden als die Menge aller Elementepaare (x | y), für die y = f(x). Der Graph einer stetigen Funktion auf einem zusammenhängenden Intervall z. B. bildet eine zusammenhängende Kurve (genauer: die Menge der Punkte der Kurve, aufgefasst als Unterraum des topologischen Raumes
, kann man visualisieren, indem man ihren Graphen in ein (zweidimensionales) Koordinatensystem zeichnet. Der Funktionsgraph einer Funktion f kann mathematisch definiert werden als die Menge aller Elementepaare (x | y), für die y = f(x). Der Graph einer stetigen Funktion auf einem zusammenhängenden Intervall z. B. bildet eine zusammenhängende Kurve (genauer: die Menge der Punkte der Kurve, aufgefasst als Unterraum des topologischen Raumes 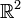 ist zusammenhängend).
ist zusammenhängend).Analog kann man Funktionen
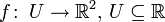 , und
, und 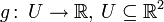 , visualisieren, indem man sie in ein dreidimensionales Koordinatensystem zeichnet. Ist f stetig, so ergibt sich eine Kurve (die auch Ecken haben kann), die sich durch das Koordinatensystem „schlängelt“. Ist g stetig, so ergibt sich eine Fläche als Bild, typischerweise in Form einer „Gebirgslandschaft“.
, visualisieren, indem man sie in ein dreidimensionales Koordinatensystem zeichnet. Ist f stetig, so ergibt sich eine Kurve (die auch Ecken haben kann), die sich durch das Koordinatensystem „schlängelt“. Ist g stetig, so ergibt sich eine Fläche als Bild, typischerweise in Form einer „Gebirgslandschaft“.Computerprogramme zur Darstellung von Funktionen heißen Funktionenplotter. Funktionsprogramme gehören auch zum Funktionsumfang von Computeralgebrasystemen (CAS), matrizenfähigen Programmierumgebungen wie MATLAB, Scilab, GNU Octave und anderen Systemen. Die wesentlichen Fähigkeiten eines Funktionenplotters sind auch auf einem graphikfähigen Taschenrechner verfügbar.
Wichtige Begriffe
- Das Bild eines Elements a der Definitionsmenge ist einfach f(a).
- Das Bild einer Funktion ist die Menge der Bilder aller Elemente der Definitionsmenge A, also
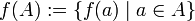 . Das Bild ist folglich eine Teilmenge der Zielmenge.
. Das Bild ist folglich eine Teilmenge der Zielmenge. - Das Urbild eines Elements b der Zielmenge ist die Menge aller Elemente des Definitionsbereichs, deren Bild b ist. Man schreibt
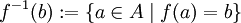 .
. - Das Urbild einer Teilmenge T der Zielmenge ist die Menge aller Elemente des Definitionsbereichs, deren Bild Element dieser Teilmenge ist:
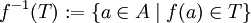 .
. - Die Umkehrfunktion einer bijektiven Funktion weist jedem Element der Zielmenge das Urbildelement zu (siehe unten).
- Als Verkettung oder Komposition zweier Funktionen f,g definiert man die Funktion, die durch Hintereinanderausführung
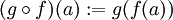 für alle Elemente a des Definitionsbereichs gegeben ist.
für alle Elemente a des Definitionsbereichs gegeben ist. - Mit BA oder AB wird die Menge aller Abbildungen von A nach B bezeichnet:
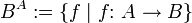 .
.
- Die Einschränkung einer Funktion
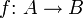 auf eine Teilmenge C des Definitionsbereichs A ist die Funktion
auf eine Teilmenge C des Definitionsbereichs A ist die Funktion 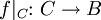 , die (je nach Definition) gegeben ist durch
, die (je nach Definition) gegeben ist durch
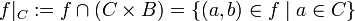 bzw.
bzw.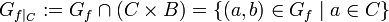 .
.
- Ein Fixpunkt ist ein Element a des Definitionsbereichs von f, für das f(a) = a gilt.
Eigenschaften von Funktionen
Allgemeine Eigenschaften
- Eine Funktion ist injektiv, wenn jedes Element des Wertebereichs höchstens ein Urbild hat. D. h. aus f(x1) = y = f(x2) folgt x1 = x2.
- Sie ist surjektiv, wenn jedes Element der Zielmenge mindestens ein Urbild hat. D. h. zu beliebigem y gibt es ein x, so dass f(x) = y.
- Sie ist bijektiv, wenn sie injektiv und surjektiv ist, also wenn jedes Element der Zielmenge genau ein Urbild hat.
- Sie ist idempotent, wenn
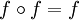 ist, d. h.
ist, d. h. 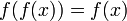 für alle Elemente x des Definitionsbereichs gilt.
für alle Elemente x des Definitionsbereichs gilt. - Sie ist eine Involution, wenn
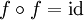 ist, also
ist, also 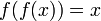 für alle Elemente x des Definitionsbereichs gilt.
für alle Elemente x des Definitionsbereichs gilt.
Eigenschaften, die in der Analysis von Interesse sind
- Konstanz
- Identität
- Beschränktheit
- Periodizität
- Monotonie
- Geradheit
- Stetigkeit
- Differenzierbarkeit
- Glattheit
- Holomorphie
- Homogenität
- Messbarkeit
- Integrierbarkeit
- Konvexität
Funktionen, die Strukturen beachten
Funktionen, die auf Zusammenhänge wie z. B. Operationen (Addition, etc.) in der Definitions- und der Zielmenge „Rücksicht nehmen“, werden Morphismen genannt. Siehe Homomorphismus, Kategorientheorie.
Strukturen erzeugende Abbildungen
Ein fundamentales Konzept in der Mathematik stellen Strukturen dar, die dadurch entstehen, dass Mengen in Verbindung mit dazu gehörigen Abbildungen gesehen werden. Derartige Strukturen bilden die Grundlage praktisch aller mathematischen Disziplinen, sobald sie über elementare Mengenlehre, kombinatorische Probleme oder grundlegende mathematisch-philosophische Fragestellungen hinausgehen.
Algebraische Strukturen
Mengen können durch sogenannte Verknüpfungen strukturiert werden. Der wichtigste Spezialfall ist die innere zweistellige Verknüpfung, dabei handelt es sich um eine Abbildung der Form
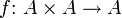 .
.Beispiele für innere zweistellige Verknüpfungen sind Rechenoperationen, wie die Addition oder Multiplikation auf Zahlenmengen. Dementsprechend wird das Bild * (x,y) eines Paares (x,y) unter einer Verknüpfung * üblicherweise in der Form x * y geschrieben.
Ist auf der Menge B eine innere zweistellige Verknüpfung * gegeben, so lässt sich auch auf BA eine innere zweistellige Verknüpfung von Abbildungen
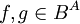 definieren:
definieren:Eine zweite wichtige Art der Abbildung ist die äußere zweistellige Verknüpfung, dies ist eine Abbildung der Form
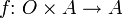 oder
oder 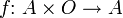 . O wird dabei als Operatorenbereich bezeichnet.
. O wird dabei als Operatorenbereich bezeichnet.Wichtigste Beispiele hierfür sind Module über Ringen und Vektorräume.
Topologische Strukturen
Eine topologische Struktur oder ein topologischer Raum besteht aus einer nichtleere Menge X und einem ein Mengensystem sogenannter offener Mengen, einer Topologie. Eine Topologie kann definiert werden mittels einer Abbildung
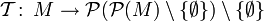 ,
,
mit
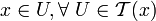 ,
,- aus
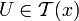 und
und 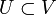 folgt:
folgt: 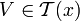 ,
, - aus
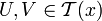 folgt:
folgt: 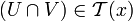 ,
, - ist
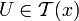 , so existiert ein
, so existiert ein 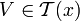 , so dass
, so dass 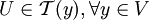 .
.
Die Mengen
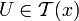 werden als Umgebungen von x bezeichnet.
werden als Umgebungen von x bezeichnet. 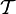 ordnet also jedem Element einer Menge die Menge seiner Umgebungen zu.
ordnet also jedem Element einer Menge die Menge seiner Umgebungen zu.In der Analysis werden üblicherweise topologische Räume betrachtet, deren topologische Struktur durch eine sogenannte Abstandsfunktion oder Metrik erzeugt wird. Eine Metrik ist dabei eine Abbildung
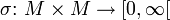 , mit den folgenden Eigenschaften:
, mit den folgenden Eigenschaften: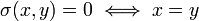 ,
,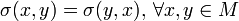 ,
,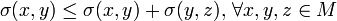 (Dreiecksungleichung).
(Dreiecksungleichung).
Anschaulich gesprochen, gibt eine Metrik also den Abstand zweier Elemente an.
Handelt es sich bei der zu betrachtenden Menge um einen Vektorraum V über dem reellen oder komplexen Zahlenkörper
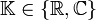 , so kann eine Metrik (und damit eine Topologie) mittels einer Norm erzeugt werden. Eine Norm ist eine Abbildung
, so kann eine Metrik (und damit eine Topologie) mittels einer Norm erzeugt werden. Eine Norm ist eine Abbildung , mit
, mit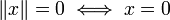 ,
,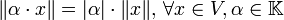 (dabei sei | α | der Betrag von α),
(dabei sei | α | der Betrag von α),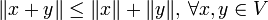 (Dreiecksungleichung).
(Dreiecksungleichung).
(Die Definition gilt in analoger Weise für Moduln aller Art.)
Anschaulich kann die Norm eines Vektors als seine Länge interpretiert werden. Abschwächungen des Normbegriffes sind Halbnormen und Quasi-Normen, mittels derer sich ebenfalls topologische Strukturen (allerdings keine Metriken) definieren lassen.
Sesquilinearformen
sind in der linearen Algebra und Funktionalanalysis betrachtete Abbildungen, die eine topologische und insbesondere geometrische Struktur erzeugen können.
Ist V ein Vektorraum über dem reellen oder komplexen Zahlenkörper
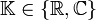 , so ist eine Sesquilinearform eine Abbildung
, so ist eine Sesquilinearform eine Abbildung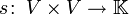 , mit den Eigenschaften
, mit den Eigenschaften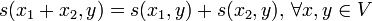 ,
,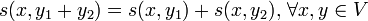 ,
,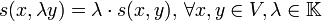 ,
,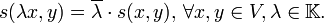
Man sagt, s ist linear in der zweiten und antilinear (oder auch semilinear) in der ersten Komponente. Diese Anordnung ist allerdings willkürlich und variiert von Autor zu Autor.
Erfüllt die quadratische Form q(x): = s(x,x) von s zusätzlich die Bedingung
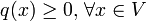 , oder gar
, oder gar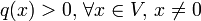 ,
,
so nennt man s positiv semidefinit bzw. positiv definit.
Ist V ein komplexer Vektorraum, so bezeichnet man s in diesen Fällen schlicht als positiv, bzw. strikt positiv und es folgt, dass die Sesquilinearform hermitesch ist, d. h. es gilt
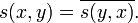
Ist V ein reeller Vektorraum, so nennt man eine Sesquilinearform, die die entsprechende Bedingung
s(x,y) = s(y,x) erfüllt, symmetrisch. Die Symmetrie einer Sesquilinearform folgt nicht aus ihrer Definitheit.
Eine positive (bzw. positiv semidefinite und symmetrische) Sesquilinearform bezeichnet man als Semiskalarprodukt, eine strikt positive (bzw. positiv definite und symmetrische) Sesquilinearform als Skalarprodukt. Im zweiten Fall schreibt man
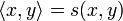 .
.Jedes Skalarprodukt (bzw. Semiskalarprodukt) erzeugt mittels
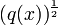 eine Norm (bzw. Halbnorm), also eine topologische Struktur.
eine Norm (bzw. Halbnorm), also eine topologische Struktur.Zusätzlich lässt sich mittels eines Skalarproduktes der Begriff der Orthogonalität definieren. Zwei Vektoren x,y heißen orthogonal genau dann, wenn
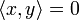 gilt.
gilt.Spezielle Funktionen und Funktionstypen
Es gibt unterschiedlichste Unterscheidungsmerkmale und somit auch viele Namen für einzelne Funktionstypen.
Analytische Funktionen
- Algebraische Funktionen: Man nennt eine Funktion w = w(z) algebraisch, wenn sie Lösung einer algebraischen Gleichung
-
- ist, wobei das Polynom
- über
 irreduzibel ist.[1]Zu der Menge der algebraischen Funktionen gehören unter anderem alle Funktionen, die sich aus einer Verknüpfung der Grundrechenarten und Radizieren zusammensetzen. Es existieren aber auch algebraische Funktionen, die sich auf diese Weise nicht darstellen lassen (siehe Galoistheorie).
irreduzibel ist.[1]Zu der Menge der algebraischen Funktionen gehören unter anderem alle Funktionen, die sich aus einer Verknüpfung der Grundrechenarten und Radizieren zusammensetzen. Es existieren aber auch algebraische Funktionen, die sich auf diese Weise nicht darstellen lassen (siehe Galoistheorie).
- homogene lineare Funktion (auch: Proportionalität): allgemein beschrieben durch f(x) = mx; ist ein Homomorphismus bezüglich der Addition
- allgemeine lineare Funktion (oder affine Funktion): allg. beschrieben durch f(x) = ax + b; siehe auch affine Abbildung
- Quadratische Funktion: allg. beschrieben durch f(x) = ax2 + bx + c (s. Quadratische Gleichung)
- Kubische Funktion
- Potenzfunktion
- Polynom-Funktion; auch ganzrationale Funktion: allg. beschrieben durch
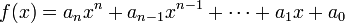 oder
oder
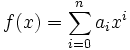
- Rationale Funktion; gebrochen-rationale Funktion: Quotient zweier Polynom-Funktionen, f(x) = g(x) / h(x)
- Wurzelfunktion: besteht aus gebrochenrationalen Funktionen, verknüpft durch die Grundrechenarten und Wurzelausdrücke
- Transzendente Funktionen: Eine mathematische Funktion nennt man transzendent, wenn sie nicht algebraisch ist. Hierzu zählen:
- Exponentialfunktion
- Logarithmus
- Kreis- und Hyperbelfunktionen
- Spezielle Funktionen
- sonstige Funktionen
Reelle Funktionen, die nicht analytisch sind
Weitere Funktionen
- Charakteristische Funktion
- Vorzeichenfunktion
- Primitiv-rekursive Funktion
- Ackermannfunktion
- Phifunktion
- Zahlentheoretische Funktion
- Fehlerfunktion
- Lokal konstante Funktion
- Dirichlet-Funktion
Verallgemeinerungen
Partielle Funktionen
Vom Begriff der Funktion wohl zu unterscheiden ist der Begriff der partiellen Funktion der theoretischen Informatik, in der Mathematik spricht man eher von „nicht überall definierten Funktionen“. Hier darf es Elemente der Quellmenge (x-Werte) geben, denen kein Wert der Zielmenge (y-Wert) zugeordnet ist. Hier ist dann die Nennung der Quellmenge in der obigen Tripelschreibweise tatsächlich notwendig. Allerdings darf es auch dort für einen x-Wert nicht mehr als einen y-Wert geben. Um partielle Funktionen von Funktionen zu unterscheiden, bezeichnet man letztere auch als totale oder überall definierte Funktionen.
Mengentheoretisch lassen sich partielle Funktionen als Paare f = (f',D), bestehend aus einer (totalen) Funktion
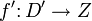 (wobei f' als Relation oder als Paar von einer Relation und einer Zielmenge gegeben ist) und einer echten Obermenge
(wobei f' als Relation oder als Paar von einer Relation und einer Zielmenge gegeben ist) und einer echten Obermenge 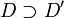 von D', definieren. Ist eine (totale) Funktion als Tripel f' = (Gf',D',Z) festgelegt, dann ist eine partielle Funktion ein Tripel f = (Gf',D,Z) mit einer Menge
von D', definieren. Ist eine (totale) Funktion als Tripel f' = (Gf',D',Z) festgelegt, dann ist eine partielle Funktion ein Tripel f = (Gf',D,Z) mit einer Menge 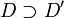 .
.Funktionen mit Werten in einer echten Klasse
Häufig liegen die Werte einer Funktion nicht in einer Zielmenge, sondern lediglich in einer echten Klasse, beispielsweise sind Mengenfolgen „Funktionen“ mit Definitionsbereich
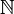 und Werten in der Allklasse. Um die mengentheoretischen Probleme, die sich daraus ergeben, zu vermeiden, betrachtet man nur noch den Graph der entsprechenden Funktion, genauer: Ein funktionsartiger Graph ist eine Menge G von Paaren (x,y), so dass keine zwei Paare im ersten Eintrag übereinstimmen:[2]
und Werten in der Allklasse. Um die mengentheoretischen Probleme, die sich daraus ergeben, zu vermeiden, betrachtet man nur noch den Graph der entsprechenden Funktion, genauer: Ein funktionsartiger Graph ist eine Menge G von Paaren (x,y), so dass keine zwei Paare im ersten Eintrag übereinstimmen:[2]Definitions- und Wertemenge sind tatsächlich Mengen, aber es ist nicht nötig, sich von vornherein auf eine Zielmenge festzulegen.
Einzelnachweise
- ↑ J. Naas, H. L. Schmid: Mathematisches Wörterbuch. B. G. Teubner, Stuttgart 1979, ISBN 3-519-02400-4,
- ↑ N. Bourbaki, Elements de Mathematiques, Theorie des Ensembles, II
Literatur
- Heinz-Dieter Ebbinghaus: Einführung in die Mengenlehre. Spektrum Akademischer Verlag, Heidelberg–Berlin 2003. ISBN 3-8274-1411-3.
- Paul R. Halmos: Naive Mengenlehre. Vandenhoeck & Ruprecht, Göttingen 1968. ISBN 3-525-40527-8.
- Harro Heuser: Funktionalanalysis: Theorie und Anwendung. 3. Aufl., B.G. Teubner, Stuttgart 1992. ISBN 3-519-22206-X.
- Arnold Oberschelp: Allgemeine Mengenlehre. Mannheim–Leipzig–Wien–Zürich 1994.
Siehe auch
- Frege: Funktion und Begriff (der Begriff als Funktion)
- Funktionenplotter (zur graphischen Darstellung)
- Funktionsschar
- Funktion höherer Ordnung
Weblinks
Wikimedia Foundation.

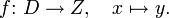
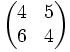

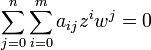
![\sum_{j=0}^n\sum_{i=0}^m a_{ij}X_1^i X_2^j\in \mathbb C[X_1,X_2]](/pictures/dewiki/49/179b4e60c694b9b239872a6429d1772c.png)