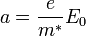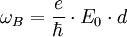Blochoszillation

Als Bloch-Oszillationen bezeichnet man die Oszillation von Ladungsträgern in Festkörpern unter der Wirkung eines statischen elektrischen Feldes.

Ursache für diese Oszillationen ist der Zusammenhang zwischen der effektiven Masse eines Ladungsträger und der Dispersionsrelation in einem periodischen Potenzial.

Die Masse von Ladungsträgern in kristallinen Festkörpern ist wesentlich von den periodischen Eigenschaften des Gitters abhängig. Auch Richtung (Anisotropie) und Betrag (Dispersion) der Ladungsträger-Geschwindigkeit relativ zum Kristallgitter haben einen Einfluss auf die effektive Masse. Für die einfache Näherung eines anisotropen Festkörpers ist diese umgekehrt proportional zur Krümmung (d.h. zur zweiten "Ableitung") der Dispersionskurve:

$m^{*} = \hbar^2 \cdot \left[ {{d^2 \varepsilon(k)} \over {d k^2}} \right]^{-1}$

Die effektive Masse kann beliebige reelle Werte annehmen, insbesondere auch negativ werden. Ein von außen angelegtes konstantes elektrisches Feld E₀ führt nun zu einer Beschleunigung der Ladungsträger

$a = {e \over m^{*}} E_0$

Wird dabei der Impuls so groß, dass die effektive Masse negativ wird, so führt eine weitere Krafteinwirkung nicht zu weiterer Beschleunigung, sondern zur Abbremsung, gefolgt von einer Beschleunigung in die umgekehrte Richtung. Da die Dispersionsrelation symmetrisch bezüglich positiver und negativer Impulse ist, wird dann wieder ein Umkehrpunkt bei negativem Impuls erreicht, es findet also eine Oszillation statt. Die Oszillationsperiode

$\omega_B = {e\over\hbar}\cdot E_0 \cdot d$

ist proportional zur Stärke E₀ des angelegten externen Feldes und zur Gitterperiode d des Festkörpers. Diese Oszillation von elektrischer Ladung verursacht elektromagnetische Strahlung, die prinzipiell messbar ist.

In natürlichen Festkörpern ist ω_B aufgrund der verhältnismäßig kleinen Gitterperioden selbst bei sehr starken elektrischen Feldern nicht ausreichend hoch, als dass die Ladungsträger innerhalb von Streu- und Tunnelzeiten vollständige Oszillationen durchführen können. Der experimentelle Nachweis von Bloch-Oszillationen konnte daher seit ihrer theoretischen Vorhersage durch Leo Esaki im Jahre 1970 lange Zeit nicht erbracht werden. Erst die Fortschritte in der Halbleitertechnologie der vergangenen Jahre und Jahrzehnte ermöglichten unter Verwendung künstlicher Halbleiter (sogenannter Halbleiterübergitter) die Herstellung von Strukturen mit genügend großen Übergitterperioden. In solchen Strukturen ist die Periode der Oszillationen kleiner als die Streuzeiten der Elektronen, so dass innerhalb der Streuzeit mehrere Oszillationen in einem zeitaufgelösten Experiment beobachtet werden können. Die Beobachtung von Bloch Oszilationen in Übergittern gelang erstmals bei Temperaturen nahe dem absoluten Nullpunkt (Jochen Feldmann, 1992; Karl Leo, 1992). Ein wichtiger Meilenstein war die Beobachtung von kohärenter Terahertzstrahlung von Bloch Oszillationen (Hartmut Roskos, 1993). Bei Raumtemperatur konnten Bloch Oszillationen ebenfalls experimentell nachgewiesen werden (Thomas Dekorsy,1995).

Ein weiteres System, in dem sich Bloch-Oszillationen verhältnismäßig einfach beobachten lassen, sind optische Gitter für neutrale Atome ^[1].

Potentielle Anwendung finden Bloch-Oszillationen in elektronischen Bauelementen zur Erzeugung von Terahertz-Strahlung. Allerdings ist es bis heute nicht gelungen, ein elektrisches Bauelement zu realisieren, dass aufgrund von Bloch-Oszillationen Terahertz-Strahlung aussendet.

Einzelnachweise

• J. Feldmann et al.: Optical Investigation of Bloch Oscillations in a Semiconductor Superlattice. Physical Review B 46, 7252 (1992).
• K. Leo, et al.: Observation of Bloch Oscillations in a Semiconductor Superlattice. Solid State Communications 84, 7252 (1992).
• C. Waschke et al.: Coherent Submillimeter-Wave Emission from Bloch Oscillations in a Semiconductor Superlattice. Physical Review Letters 70, 3319 (1993).
• T. Dekorsy et al.: Bloch Oscillations at Room-Temperature. Physical Review 51, 17275 (1995).

1. ↑ Beispiel für Blochoszillationen in einem Bose-Einstein Kondensat: Physical Review Letters 100, 080405 (2008).