- Bornologisch
-
Bornologische Räume sind in dem mathematischen Teilgebiet Funktionalanalysis spezielle lokalkonvexe Räume, für deren lineare Operatoren die aus der Theorie der normierten Räume bekannte Äquivalenz von Stetigkeit und Beschränktheit gilt. Diese Räume lassen sich durch ihre Nullumgebungsbasen charakterisieren und haben weitere Eigenschaften mit normierten Räumen gemeinsam.
Inhaltsverzeichnis
Motivation
Eine Teilmenge A eines lokalkonvexen K-Vektorraums E heißt beschränkt, wenn sie von jeder Nullumgebung absorbiert wird, d.h. zu jeder Nullumgebung
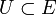 gibt es ein
gibt es ein 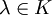 mit
mit 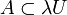 .
.Eine Teilmenge B eines lokalkonvexen K-Vektorrraums heißt Bornolog, wenn folgende Bedingungen erfüllt sind:
- B ist absolutkonvex, d.h. für
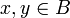 und
und 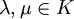 mit
mit 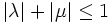 gilt
gilt 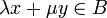 .
. - B absorbiert jede beschränkte Menge, d.h. zu jeder beschränkten Menge
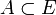 gibt es ein
gibt es ein 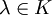 mit
mit 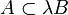 .
.
Leicht zeigt man, dass jeder lokalkonvexe Raum eine Nullumgebungsbasis aus Bornologen besitzt. Ist umgekehrt jeder Bornolog eine Nullumgebung, so nennt man den Raum bornologisch.
Beispiele
- Jeder metrisierbare lokalkonvexe Raum E ist bornologisch. Ist nämlich B ein Bornolog in E,
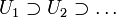 eine abzählbare Nullumgebungsbasis von E, und nimmt man an, dass B keine Menge der Form
eine abzählbare Nullumgebungsbasis von E, und nimmt man an, dass B keine Menge der Form 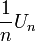 enthält, so kann man ein
enthält, so kann man ein 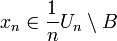 wählen. Dann konvergiert
wählen. Dann konvergiert 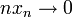 , d.h.
, d.h. 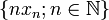 ist kompakt und daher beschränkt, also in einer Menge der Form λB enthalten. Für
ist kompakt und daher beschränkt, also in einer Menge der Form λB enthalten. Für 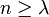 folgt der Widerspruch
folgt der Widerspruch 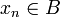 . Also ist B eine Nullumgebung.
. Also ist B eine Nullumgebung.
- Ist E ein normierter Raum ungleich {0}, so ist
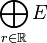 mit der Finaltopologie ein Beispiel für einen bornologischen Raum, der nicht metrisierbar ist.
mit der Finaltopologie ein Beispiel für einen bornologischen Raum, der nicht metrisierbar ist.
Vererbungseigenschaften
Ein Induktiver Limes bornologischer Räume ist wieder bornologisch.
Beschränkte Operatoren
Wie in der Theorie der normierten Räume heißt ein linearer Operator zwischen lokalkonvexen Vektorräumen beschränkt, wenn er beschränkte Mengen wieder auf beschränkte Mengen abbildet.
Für einen lokalkonvexen Raum E sind äquivalent:
- E ist bornologisch
- Jeder beschränkte Operator
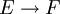 in einen weiteren lokalkonvexen Raum F ist stetig.
in einen weiteren lokalkonvexen Raum F ist stetig.
Ein linearer Operator
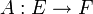 heißt folgenstetig, wenn aus
heißt folgenstetig, wenn aus 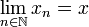 in E stets
in E stets 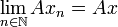 in F folgt. In nicht-metrisierbaren Räumen kann diese Bedingung echt schwächer als Stetigkeit sein.
in F folgt. In nicht-metrisierbaren Räumen kann diese Bedingung echt schwächer als Stetigkeit sein.Für einen bornologischen Raum E und einen linearen Operator
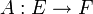 sind äquivalent:
sind äquivalent:- A ist stetig.
- A ist folgenstetig.
- A ist beschränkt.
Bornologische Räume als induktive Limiten normierter Räume
Ein lokalkonvexer Raum E heißt eine induktiver Limes normierter Räume, wenn es lineare Abbildungen
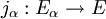 mit normierten Räumen Eα gibt, so dass
mit normierten Räumen Eα gibt, so dass 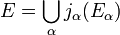 und die Topologie auf E die feinste lokalkonvexe Topologie ist, die alle jα stetig macht.
und die Topologie auf E die feinste lokalkonvexe Topologie ist, die alle jα stetig macht.Für einen lokalkonvexen Raum E sind äquivalent:
- E ist bornologisch.
- E ist ein induktiver Limes normierter Räume.
Man kann einen solchen induktiven Limes sogar angeben. Für eine beschränkte und absolutkonvexe Menge
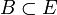 sei
sei 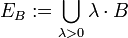 . Dann ist EB ein Vektorraum, und das Minkowski-Funktional pB zu
. Dann ist EB ein Vektorraum, und das Minkowski-Funktional pB zu 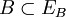 macht diesen Vektorraum zu einem normierten Raum. Der lokalkonvexe Raum E ist genau dann bornologisch, wenn er die induktive lokalkonvexe Topologie aller Inklusionen
macht diesen Vektorraum zu einem normierten Raum. Der lokalkonvexe Raum E ist genau dann bornologisch, wenn er die induktive lokalkonvexe Topologie aller Inklusionen 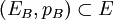 trägt, wobei B die beschränkten, absolutkonvexen Mengen durchläuft.
trägt, wobei B die beschränkten, absolutkonvexen Mengen durchläuft.Kann man für E sogar eine Darstellung als induktiven Limes von Banachräumen finden, so nennt man E ultrabornologisch. In solchen Räumen gelten der Satz über die offene Abbildung und der Satz vom abgeschlossenen Graphen.
Vollständigkeit des Dualraums
Ist E ein lokalkonvexer Vektorraum, so definiert jede beschränkte Menge B in E eine Halbnorm PB auf dem Dualraum
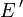 , indem man
, indem man 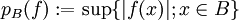 setzt. Versehen mit der Menge der Halbnormen pB, wobei B die beschränkten Mengen von E durchläuft, wird
setzt. Versehen mit der Menge der Halbnormen pB, wobei B die beschränkten Mengen von E durchläuft, wird 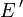 zu einem lokalkonvexen Vektorraum, den man dann mit Eb' bezeichnet. Dies verallgemeinert die Dualraumbildung bei normierten Räumen. Wie in der Theorie der normierten Räume gilt folgender Satz:
zu einem lokalkonvexen Vektorraum, den man dann mit Eb' bezeichnet. Dies verallgemeinert die Dualraumbildung bei normierten Räumen. Wie in der Theorie der normierten Räume gilt folgender Satz:Ist E bornologisch, so ist Eb' vollständig, d.h. jedes Cauchy-Netz konvergiert.
Literatur
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8
- B ist absolutkonvex, d.h. für
Wikimedia Foundation.
