Distinguierter Raum

In der mathematischen Disziplin der Funktionalanalysis werden lokalkonvexe Räume, das sind Vektorräume mit einer topologischen Struktur, untersucht. Die wichtige topologische Eigenschaft der Metrisierbarkeit lässt sich in lokalkonvexen Räumen durch die Nullumgebungsbasen charakterisieren. Da die Vervollständigung eines metrisierbaren und lokalkonvexen Raumes ein Fréchet-Raum ist, nennt man solche Räume auch prä-F-Raum.

Charakterisierung

Ein lokal konvexer Raum E ist genau dann metrisierbar, wenn er eine abzählbare Nullumgebungsbasis hat.

Ist nämlich 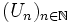$(U_n)_{n\in{\mathbb N}}$ eine abzählbare Nullumgebungsbasis, so kann man die U_n ohne Einschränkung als absolutkonvex annehmen. 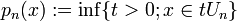$p_n(x) := \inf\{t>0; x\in tU_n\}$ definiert dann eine Halbnorm auf E, und 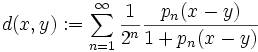$d(x,y):=\sum_{n=1}^\infty \frac{1}{2^n} \frac{p_n(x-y)}{1+p_n(x-y)}$ ist eine Metrik, die die Topologie auf E erzeugt. Die Umkehrung ist klar, da in einem metrischen Raum jeder Punkt eine abzählbare Umgebungsbasis hat.

Beispiele

• Normierte Räume sind metrisierbar und lokalkonvex.
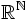• ${\mathbb R}^{\mathbb N}$ mit der Produkttopologie ist ein Beispiel für einen metrisierbaren, lokalkonvexen Raum, der nicht normierbar ist.
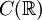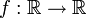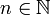• Sei $C({\mathbb R})$ der Vektorraum der stetigen Funktionen $f:{\mathbb R}\rightarrow {\mathbb R}$. Für $n\in{\mathbb N}$ sei p_n die durch 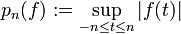$p_n(f) := \sup_{-n\le t\le n}|f(t)|$ definierte Halbnorm. Dann ist 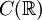$C({\mathbb R})$ mit der durch diese Halbnormen definierten Topologie metrisierbar, sogar ein Fréchetraum.

Vererbungseigenschaften

Unterräume, Quotientenräume nach abgeschlossenen Unterräumen und abzählbare Produkte von metrisierbaren, lokalkonvexen Räumen sind wieder von dieser Art.

Eigenschaften, distinguierte Räume

Metrisierbare, lokalkonvexe Räume sind bornologisch und haben daher alle Eigenschaften bornologischer Räume.

Eine beschränkte Menge in einem lokalkonvexen Vektorraum ist eine Menge B, so dass es zu jeder Nullumgebung U ein t>0 gibt mit 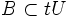$B\subset tU$. Dies darf nicht mit der Beschränktheit im metrischen Sinne verwechselt werden. Eine metrisch beschränkte Menge, d.h. eine Menge mit endlichem Durchmesser bzgl. der Metrik, muss nicht im lokalkonvexen Sinne beschränkt sein.

Ist E ein lokalkonvexer Vektorraum, so definiert jede beschränkte Menge B in E eine Halbnorm P_B auf dem Dualraum 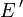$E\,'$, indem man 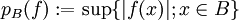$p_B(f):= \sup\{|f(x)|; x\in B\}$ setzt. Versehen mit der Menge der Halbnormen p_B, wobei B die beschränkten Mengen von E durchläuft, wird 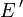$E\,'$ zu einem lokalkonvexen Vektorraum, den man dann mit E_b' bezeichnet.

Für einen metrisierbaren, lokalkonvexen Raum sind äquivalent:

• E_b' ist bornologisch.
• E_b' ist quasitonneliert.
• E_b' ist tonneliert.

Ein metrisierbarer lokalkonvexer Raum heißt distinguiert, falls er diese Bedingungen erfüllt. Normierte Räume, reflexive Frécheträume oder quasinormierbare Frécheträume sind distinguiert.

Quellen

• K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
• R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8