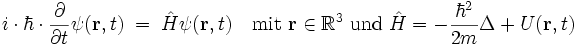- Bornsche Regel
-
Mit der Bornschen Wahrscheinlichkeitsinterpretation (benannt nach Max Born) der Quantenmechanik lassen sich Besonderheiten der Theorie erklären, die mit der klassischen Physik nicht erklärbar scheinen.
Borns probabilistische Deutung der Quantenmechanik
In der Quantenmechanik müssen vielfach Wahrscheinlichkeitsaussagen getroffen werden. Mittel der sogenannten Bornschen Regel kann die Wahrscheinlichkeit für unterschiedliche Eigenwerte einer bestimmten Observablen berechnet werden. Born hat hieran eine probabilistische Deutung des quantenmechanischen Formalismus geknüpft.
Born erklärt
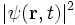 als die räumliche Dichte für die Wahrscheinlichkeit das Quantenobjekt am Ort
als die räumliche Dichte für die Wahrscheinlichkeit das Quantenobjekt am Ort 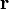 zur Zeit t zu detektieren. So kann zwar nicht der genaue Aufenthaltsort des Teilchens, aber die so genannte Wahrscheinlichkeitsdichte
zur Zeit t zu detektieren. So kann zwar nicht der genaue Aufenthaltsort des Teilchens, aber die so genannte Wahrscheinlichkeitsdichte 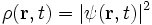 vorhergesagt werden. Diese Wahrscheinlichkeitsdichte lässt sich bei einer Gruppe (Ensemble) von so genannten „gleichpräparierten Zuständen“ (Teilchen mit gleichen Eigenschaften) als relative Häufigkeitsverteilung deuten. (Früher wurde
vorhergesagt werden. Diese Wahrscheinlichkeitsdichte lässt sich bei einer Gruppe (Ensemble) von so genannten „gleichpräparierten Zuständen“ (Teilchen mit gleichen Eigenschaften) als relative Häufigkeitsverteilung deuten. (Früher wurde 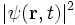 fälschlicherweise als Massen- oder Ladungsdichte interpretiert.)
fälschlicherweise als Massen- oder Ladungsdichte interpretiert.)Borns Erklärung des Welle-/Teilchen-Dualismus
Quantenobjekte, zum Beispiel Photonen und Elektronen, zeigen bei verschiedenen Experimenten sowohl Wellen- als auch Teilcheneigenschaften.
Nach der Bornschen Interpretation breitet sich ein Quantenobjekt, das durch die Wellenfunktion
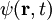 beschrieben wird, mit Welleneigenschaften aus. Die Wellenfunktion
beschrieben wird, mit Welleneigenschaften aus. Die Wellenfunktion 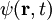 muss die Schrödingergleichung
muss die Schrödingergleichungerfüllen. Somit werden Welleneigenschaften (bei Ausbreitung) und Teilcheneigenschaften (bei Detektion) von Quantenobjekten mit Hilfe der Wellenfunktion
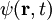 zusammengefasst.
zusammengefasst.Literatur
- Max Born: Zur Quantenmechanik der Stoßvorgänge, in: Zeitschrift für Physik 37/12 (1926), 863–867.
- Jenann Ismael: „Quantum Mechanics“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
Wikimedia Foundation.