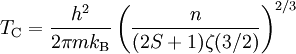Bose-Einstein-Kondensation

Das Bose-Einstein-Kondensat ist ein extremer Aggregatzustand eines Systems ununterscheidbarer Teilchen, in dem sich der überwiegende Anteil der Teilchen im selben quantenmechanischen Zustand befindet. Dies ist nur möglich, wenn die Teilchen Bosonen sind und somit der Bose-Einstein-Statistik unterliegen.

Bose-Einstein-Kondensate sind makroskopische Quantenobjekte, in denen die einzelnen Bosonen vollständig delokalisiert sind. Die Wahrscheinlichkeit jedes Bosons, es an einem bestimmten Punkt anzutreffen, ist also überall innerhalb des Kondensates gleich. Der Zustand kann daher durch eine einzige Wellenfunktion beschrieben werden. Daraus resultieren Eigenschaften wie Suprafluidität, Supraleitung oder Kohärenz über makroskopische Entfernungen. Letztere erlaubt Interferenzexperimente mit Bose-Einstein-Kondensaten sowie die Herstellung eines Atomlasers, den man durch kontrollierte Auskopplung eines Teils der Materiewelle aus der das Kondensat haltenden Falle erhalten kann.

Überblick

Theoretisch wurde dieser Zustand schon 1924 von Satyendranath Bose und Albert Einstein vorhergesagt.

Im August 2005 wurde in der Tat am Lorentz-Institut für Theoretische Physik der niederländischen Universität Leiden das 16-seitige Manuskript „Quantentheorie des einatomigen idealen Gases – Zweite Abhandlung“ von Einstein aus dem Jahre 1924 entdeckt, in dem die Kondensation eines idealen homogenen bosonischen Gases beim absoluten Nullpunkt (-273,15 Grad Celsius 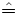$\,\hat =\,$ 0 K) vorhergesagt wird. Sowohl Manuskript als auch Originalartikel können bei der Universität Leiden heruntergeladen werden (siehe Weblink).

Die erstaunlichen Eigenschaften von flüssigem Helium bei tiefen Temperaturen wurden auf Bose-Einstein-Kondensation zurückgeführt, allerdings ist die direkte Beobachtung des Effekts in diesem System aufgrund der Wechselwirkung zwischen den Teilchen ausgesprochen schwierig. Auch Versuche, Bose-Einstein-Kondensation in einem Gas aus polarisierten Wasserstoffatomen zu erreichen, führten zunächst nicht zum Erfolg. Erst 1995 wurde experimentell das erste Bose-Einstein-Kondensat in einer magnetischen TOP-Falle hergestellt. Im Jahr 2001 erhielten Eric A. Cornell, Wolfgang Ketterle und Carl E. Wieman den Nobelpreis für Physik für die Herstellung des ersten Bose-Einstein-Kondensats aus einem Gas von Rubidium- bzw. Natriumatomen.

Der Phasenübergang von einem klassischen atomaren Gas zu einem Bose-Einstein-Kondensat findet statt, wenn eine kritische Phasenraumdichte erreicht wird, das bedeutet, dass die Dichte der Teilchen mit fast gleichem Impuls groß genug ist. Anschaulich kann man dies so verstehen: Die Atome sind Quantenteilchen, deren Bewegung durch ein Wellenpaket dargestellt wird. Die Ausdehnung dieses Wellenpakets ist die thermische de-Broglie-Wellenlänge. Diese wird umso größer, je weiter die Temperatur sinkt. Erreicht die de-Broglie-Wellenlänge den mittleren Abstand zwischen zwei Atomen, so kommen die Quanteneigenschaften zum Tragen. In einem dreidimensionalen Ensemble setzt nun die Bose-Einstein-Kondensation ein. Daher ist es notwendig, die Dichte des Gases zu erhöhen und die Temperatur zu senken, um den Phasenübergang zu erreichen.

Erzeugung

Die übliche Methode zum Erzeugen von Bose-Einstein-Kondensaten aus Atomen besteht aus zwei Phasen:

Zunächst werden die Atome in einer magneto-optischen Falle gefangen und durch Laserkühlung vorgekühlt. Die Laserkühlung jedoch besitzt ein unteres Limit für Temperaturen (ein typischer Wert ist etwa 100 µK), das durch den Rückstoß bei der spontanen Emission der Photonen bedingt ist.

Die mittlere Geschwindigkeit der so gekühlten Atome von nur noch einigen Zentimetern pro Sekunde ist jedoch gering genug, um sie in einer magnetischen oder optischen Falle zu fangen. Durch evaporative Kühlung, d. h. kontinuierliches Entfernen der energiereichsten Atome, wird die Temperatur der Atomwolke weiter gesenkt. Bei diesem Prozess werden meist über 99,9 % der Atome gezielt entfernt. So erreichen die Atome die nötige Phasenraumdichte, um den Phasenübergang in ein Bose-Einstein-Kondensat zu vollziehen.

Auf diese Weise ist es bis 2004 gelungen, bei enorm tiefen Temperaturen, 10^-7 Kelvin und tiefer, Bose-Einstein-Kondensation für eine Vielzahl verschiedener Isotope ( ⁷Li, ²³Na, ⁴¹K, ⁵²Cr, ⁸⁵Rb, ⁸⁷Rb, ¹³³Cs und ¹⁷⁴Yb) zu erreichen, und auch beim Wasserstoff war man schließlich erfolgreich, wenn auch mit etwas anderen Methoden. Der Supraflüssigkeitszustand von ⁴He bei Temperaturen unter 2,17 K gibt dagegen kein gutes Beispiel für Bose-Einstein-Kondensation, weil die Wechselwirkung zwischen den Atomen nicht vernachlässigt werden kann, sodass sich im Gegensatz zur Bose-Einstein-Theorie nicht maximal 100%, sondern nur 8% der Atome im Grundzustand befinden. Auch die Tatsache, dass die oben genannten Gase überhaupt bosonisches und nicht, wie Festkörperphysiker oder Chemiker von Alkaliatomen erwarten würden, fermionisches Verhalten zeigen, beruht auf einem sehr subtilen Zusammenspiel von Elektronenspin und Kernspin: Bei den angegebenen ultratiefen Temperaturen und entsprechend niedrigen Anregungsenergien sind der (halbzahlige!) Gesamtspin der Elektronenhülle der Atome und der ebenfalls halbzahlige Kernspin der Atome durch die (sehr schwache) Hyperfeinwechselwirkung zu einem ganzzahligen Gesamtspin des Systems gekoppelt. Nur wegen der Ganzzahligkeit des letztgenannten Spins hat man es mit Bosonen zu tun, für die das Pauli-Prinzip nicht gilt. Deshalb erwartet man nur wegen der ultratiefen Temperaturen das entsprechende quantenmechanische Verhalten, während z. B. die „Chemie“ der Systeme, d. h. das Verhalten bei Zimmertemperatur, allein durch den Spin der Elektronenhülle bestimmt wäre, weil bei diesen Temperaturen die thermischen Energien viel größer als die Hyperfeinfeld-Energien sind.

Im Jahr 2006 haben Demokritov und Mitarbeiter (siehe Demokritov, S; Demidov, V; Dzyapko, O; Melkov, G.; Serga, A; Hillebrands, B; Slavin, A: Nature 443 (2006) 430-433) schließlich Bose-Einstein-Kondensation von Magnonen (quantisierten Spinwellen) bei Zimmertemperatur erreicht, allerdings durch Anwendung von Pump-Prozessen.

Experimenteller Nachweis

Der Nachweis, dass ein Bose-Einstein-Kondensat tatsächlich erzeugt wurde, erfolgt bei den atomaren Gasen meistens mithilfe von Absorptions-Abbildung nach einer Flugzeit. Dabei wird die Falle, in der das Gas gefangen war, schlagartig abgeschaltet. Während der Flugzeit expandiert die Gaswolke. Anschließend wird sie mit resonantem Laser-Licht bestrahlt. Die Atome streuen dabei Photonen aus dem Laserstrahl, so dass der Strahl effektiv geschwächt wird, sie erzeugen also einen (Halb-)Schatten. Dieser Schattenwurf kann mit einer empfindlichen CCD-Kamera aufgenommen werden. Aus dem Schattenbild lässt sich dann die Dichteverteilung rekonstruieren. Dabei wird für asymmetrische Fallen eine anisotrope Expansion des Gases nach dem Abschalten der Falle beobachtet, während ein klassisches Gas im thermischen Gleichgewicht immer isotrop expandiert. Darüber hinaus beobachtet man in vielen Fällen eine parabelförmige Dichte-Verteilung, die sich als Konsequenz der Wechselwirkung zwischen den Atomen verstehen lässt, beim idealen Bosegas also nicht auftreten würde.

Mathematische Beschreibung

Im Rahmen der statistischen Physik lässt sich mit Hilfe der Bose-Einstein-Statistik die kritische Temperatur T_C eines sog. idealen Bosegases (ideal = wechselwirkungsfrei) berechnen, unterhalb derer die Bose-Einstein-Kondensation einsetzt:

$T_\mathrm{C} = \frac{h^2}{2\pi m k_\mathrm{B}} \left(\frac{n}{(2S+1)\zeta(3/2)}\right)^{2/3}$

Hierbei ist:

n: Teilchendichte (Anzahl der Teilchen pro Volumen)

m: Masse der Teilchen

S: Spin der Teilchen

ζ(x): Riemannsche Zetafunktion, $\zeta(3/2) \approx 2,6124$

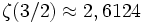
h: Plancksches Wirkungsquantum

k_B: Boltzmann-Konstante

„Freies Bosegas“ bedeutet hierbei, dass statt der in der Falle eingesperrten Atome ein unendlich ausgedehntes, homogenes Gas betrachtet wird. Der Einschluss im Fallenpotential und die Wechselwirkung zwischen den Atomen führen zu einer Abweichung der tatsächlich beobachteten kritischen Temperatur von dem vorhergesagten Wert, die Formel gibt jedoch in jedem Fall die richtige Größenordnung wieder. Für typische experimentell realisierbare Parameter findet man Temperaturen von deutlich weniger als 0,1 Mikrokelvin, sog. ultratiefe Temperaturen.

Literatur

• S. N. Bose, Z. Phys. 26, 178 (1924); englische Übersetzung erschienen in American Journal of Physics, Vol. 44, No. 11, November 1976
• A. Einstein, Sitz. Ber. Preuss. Akad. Wiss. (Berlin) 22, 261 (1924)
• Kai Bongs, Jakob Reichel, Klaus Sengstock: Bose-Einstein-Kondensation: Das ideale Quantenlabor. Physik in unserer Zeit 34(4), S. 168–176 (2003), ISSN 0031-9252

Weblinks

• BEC 2009
• Archiv von Einstein-Manuskripten an der Universität Leiden
• Max-Planck-Institut für Quantenoptik (allgemein verständliche Beschreibung, Historie)
• http://www.iap.uni-bonn.de/P2K/bec/index.html (anschauliche Erläuterungen mit vielen interaktiven Java-Applets)
• http://saftsack.fs.uni-bayreuth.de/thermo/bek.html (Online Skript mit ausführlicher theoretischer Herleitung)
• Ton-Mitschnitt eines allgemein gehaltenen Vortrags des deutschen Physiknobelpreisträgers Wolfgang Ketterle über Bose-Einstein-Kondensate (1998) (englisch)
• Video von Wolfgang Ketterles Lesung "Bose-Einstein Condensates: The Coldest Matter in the Universe" (Massachusetts Institute of Technology, 11. Oktober 2001) (englisch)

Aggregatzustände

Klassische Aggregatzustände:
Gas | Flüssigkeit | Festkörper

Nichtklassische Aggregatzustände:
Plasma | Bose-Einstein-Kondensat | Suprafluidität | Suprasolidität | mesomorpher Zustand | überkritischer Zustand | Atomgas