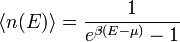- Bose-Einstein-Verteilung
-
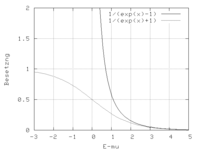 Illustration der Besetzung
Illustration der Besetzung für Bosonen (obere Kurve) bzw. Fermionen (untere Kurve) im Spezialfall der Wechselwirkungsfreiheit. Das sog. chemische Potenzial µ ist im Fermifall positiv, bei T = 0 K entspricht es der Fermienergie; im Bose-Fall ist es dagegen ein negativer Parameter, der in bestimmter Weise von Temperatur und Dichte abhängt und im Grenzfall der Bose-Einstein-Kondensation verschwinden würde.
für Bosonen (obere Kurve) bzw. Fermionen (untere Kurve) im Spezialfall der Wechselwirkungsfreiheit. Das sog. chemische Potenzial µ ist im Fermifall positiv, bei T = 0 K entspricht es der Fermienergie; im Bose-Fall ist es dagegen ein negativer Parameter, der in bestimmter Weise von Temperatur und Dichte abhängt und im Grenzfall der Bose-Einstein-Kondensation verschwinden würde.Die Bose-Einstein-Statistik und die Fermi-Dirac-Statistik sind Verteilungen in der Quantenstatistik. Sie beschreiben die mittlere Besetzungszahl
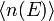 eines Quantenzustands der Energie E im thermodynamischen Gleichgewicht bei der absoluten Temperatur T für identische Bosonen bzw. Fermionen als besetzende Teilchen.
eines Quantenzustands der Energie E im thermodynamischen Gleichgewicht bei der absoluten Temperatur T für identische Bosonen bzw. Fermionen als besetzende Teilchen.Bei Wechselwirkungsfreiheit ergibt sich für Bosonen die folgende Formel:
Hierbei ist μ das sog. chemische Potential und β üblicherweise gleich 1 / (kBT) (mit der Boltzmann-Konstanten kB und der absoluten Temperatur T). Die Wahl des Faktors β hängt von der verwendeten Temperaturskala ab. Wird die Temperatur in Energieeinheiten, etwa Joule, gemessen, so beträgt er 1 / T. Dies geschieht, wenn der Faktor kB auch in der Definition der Entropie - welche dann einheitenlos ist - nicht auftaucht.
Man beachte, dass es sich um die Besetzungszahl eines Quantenzustandes handelt. Benötigt man die Besetzungszahl eines entarteten Energieniveaus, so ist obiger Ausdruck mit dem Entartungsgrad gi desselben zu multiplizieren!
Im Falle der Fermi-Dirac-Statistik erhält man im Nenner +1 anstelle von -1.
Unterhalb einer sehr tiefen kritischen Temperatur Tλ erhält man im Spezialfall der Wechselwirkungsfreiheit - unter der Annahme, dass μ gegen das Energie-Minimum strebt - die Bose-Einstein-Kondensation.
Für Fermionen existiert analog die sog. Fermi-Dirac-Statistik, die ebenso wie die Bose-Einstein-Statistik im Grenzfall großer Energie E in die Boltzmann-Statistik übergeht.
Literatur
- U. Krey, A. Owen, Basic Theoretical Physics - a Concise Overview, Berlin Heidelberg New York, Springer 2007, ISBN 978-3-540-36804-5 (auf Englisch)
- L.D. Landau, E.M. Lifschitz, Statistische Physik, Verlag Harri Deutsch, ehem. Akademie Verlag Berlin 1987. (verwendet unübliche Temperatureinheit).
Wikimedia Foundation.