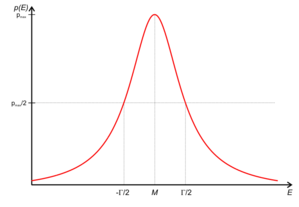
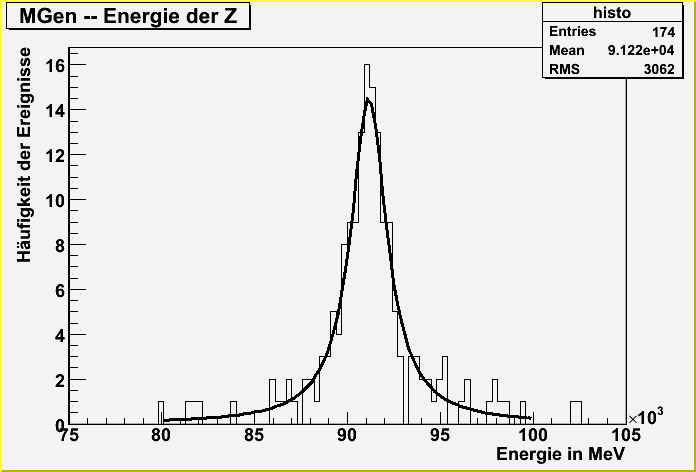
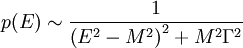Breit-Wigner-Formel — Breit Wigner Verteilung Die Breit Wigner Verteilung (nach Gregory Breit und Eugene Wigner) ist eine kontinuierliche Wahrscheinlichkeitsverteilung mit der Wahrscheinlichkeitsdichte . Γ ist die voll … Deutsch Wikipedia
Breit-Wigner-Funktion — Die Breit Wigner Funktion ist in der Mathematik auch als Cauchy Verteilung oder Lorentz Verteilung bekannt. Sie beschreibt unter anderem die Zerfallsbreite im Energiespektrum von kurzlebigen Teilchen in der Teilchenphysik. Essenziell an ihr ist… … Deutsch Wikipedia
Lorentz-Verteilung — Die Cauchy Verteilung für verschiedene Werte der beiden Parameter. Dabei gilt: γ im Bild entspricht s in der nebenstehenden Gleichung und x0 entspricht t. Die Cauchy Lorentz Verteilung (nach Augustin Louis Cauchy und Hendrik Antoon Lorentz) ist… … Deutsch Wikipedia
Cauchy-Verteilung — Die Cauchy Verteilung für verschiedene Werte der beiden Parameter. Dabei gilt: γ im Bild entspricht s in der nebenstehenden Gleichung und x0 entspricht t. Die Cauchy Lorentz Verteilung (nach Augustin Louis Cauchy und Hendrik Antoon Lorentz)… … Deutsch Wikipedia
Exponential-Verteilung — Dichte der Exponentialverteilung mit verschiedenen Werten für λ Die Exponentialverteilung ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen, die durch eine Exponentialfunktion gegeben ist. Sie wird als… … Deutsch Wikipedia
Exponentielle Verteilung — Dichte der Exponentialverteilung mit verschiedenen Werten für λ Die Exponentialverteilung ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen, die durch eine Exponentialfunktion gegeben ist. Sie wird als… … Deutsch Wikipedia
Poisson Verteilung — Die Poisson Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die beim mehrmaligen Durchführen eines Bernoulli Experiments entsteht. Letzteres ist ein Zufallsexperiment, das nur zwei mögliche Ergebnisse besitzt (z. B. „Erfolg“ und… … Deutsch Wikipedia
Benfordsche Verteilung — Das benfordsche Gesetz, auch Newcomb Benford’s Law (NBL) beschreibt eine Gesetzmäßigkeit in der Verteilung der Ziffernstrukturen von Zahlen in empirischen Datensätzen, zum Beispiel ihrer ersten Ziffern. Es lässt sich etwa in Datensätzen über… … Deutsch Wikipedia
Binomial-Verteilung — Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht… … Deutsch Wikipedia
Fisher-Verteilung — Die F Verteilung oder Fisher Verteilung (nach Ronald Aylmer Fisher) oder Fisher Snedecor Verteilung ist die Wahrscheinlichkeitsverteilung einer stetigen Zufallsvariable und ergibt sich als Quotient zweier Chi Quadrat verteilter Zufallsvariablen.… … Deutsch Wikipedia
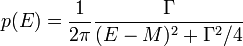 .
.