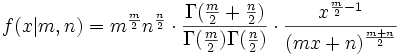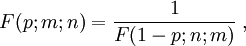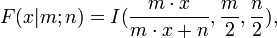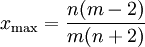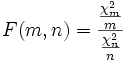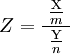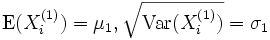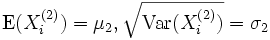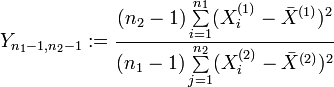- Fisher-Verteilung
-
Die F-Verteilung oder Fisher-Verteilung (nach Ronald Aylmer Fisher) oder Fisher-Snedecor-Verteilung ist die Wahrscheinlichkeitsverteilung einer stetigen Zufallsvariable und ergibt sich als Quotient zweier Chi-Quadrat-verteilter Zufallsvariablen. Sie besitzt zwei unabhängige Freiheitsgrade als Parameter und bildet so selbst eine zwei-Parameter-Verteilungsfamilie.
Als statistischer Test (F-Test) wird die F-Verteilung verwendet, um festzustellen, ob die Grundgesamtheiten zweier Stichproben in ihrer Varianz wesentlich unterscheiden (Varianzanalyse).
Inhaltsverzeichnis
Definition
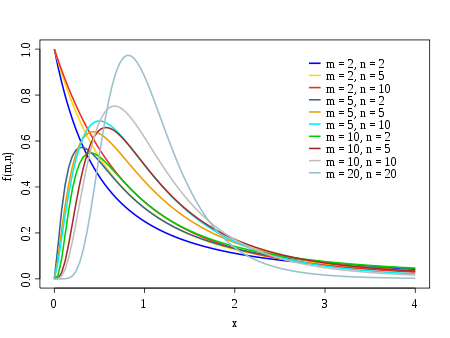
Eine stetige Zufallsvariable genügt der F-Verteilung F(m,n), wenn sie die Wahrscheinlichkeitsdichte
besitzt. Dabei ist mit Γ(x) die Gammafunktion an der Stelle x bezeichnet.
Eigenschaften
Erwartungswert
Der Erwartungswert ist nur für n > 2 definiert und lautet dann
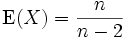 .
.
Varianz
Die Varianz ist nur für n > 4 definiert und lautet dann
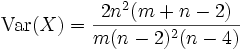 .
.
Verteilungsfunktion
Die Werte der Verteilung
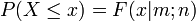 werden meist numerisch ermittelt. Man wird sie deshalb meistens einer F-Verteilungstabelle entnehmen. Eine komplette Tabellierung bezüglich aller Freiheitsgrade ist i.a. nicht notwendig, so dass die meisten Verteilungstabellen die Quantile bezüglich ausgewählter Freiheitsgrade und Wahrscheinlichkeiten angeben. Man macht sich hier auch die Beziehung zunutze:
werden meist numerisch ermittelt. Man wird sie deshalb meistens einer F-Verteilungstabelle entnehmen. Eine komplette Tabellierung bezüglich aller Freiheitsgrade ist i.a. nicht notwendig, so dass die meisten Verteilungstabellen die Quantile bezüglich ausgewählter Freiheitsgrade und Wahrscheinlichkeiten angeben. Man macht sich hier auch die Beziehung zunutze:wobei F(p;m;n) das p-Quantil der F-Verteilung mit m und n Freiheitsgraden bedeutet.
Die F-Verteilung lässt sich geschlossen ausdrücken als
wobei
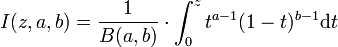 die regularisierte unvollständige Betafunktion darstellt.
die regularisierte unvollständige Betafunktion darstellt.Maximum
Für m > 2 nimmt f an der Stelle
das Maximum an.
Beziehungen zu anderen Verteilungen
Beziehung zur Beta-Verteilung
Wenn
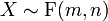 und
und 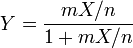 ist, dann verteilt sich
ist, dann verteilt sich 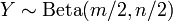
Beziehung zur Chi-Quadrat-Verteilung
Aus den
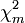 und
und 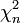 Chi-Quadrat-verteilten Zufallsgrößen mit m bzw. n Freiheitsgraden lässt sich
Chi-Quadrat-verteilten Zufallsgrößen mit m bzw. n Freiheitsgraden lässt sichkonstruieren. Dieser Ausdruck ist F-verteilt mit m und n Freiheitsgraden.
Beziehung zur nichtzentralen F-Verteilung
Für unabhängige Zufallsvariablen
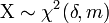 und
und 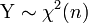 ist
istverteilt nach der nichtzentralen F-Verteilung
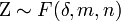 mit nichtzentralitäts-Parameter δ. Dabei ist χ2(δ,m) eine Nichtzentrale Chi-Quadrat-Verteilung mit nichtzentralitäts-Parameter δ und m Freiheitsgraden. Für δ = 0 ergibt sich die zentrale F-Verteilung F(m,n).
mit nichtzentralitäts-Parameter δ. Dabei ist χ2(δ,m) eine Nichtzentrale Chi-Quadrat-Verteilung mit nichtzentralitäts-Parameter δ und m Freiheitsgraden. Für δ = 0 ergibt sich die zentrale F-Verteilung F(m,n).Beziehung zur Normalverteilung
Wenn die identischen normalverteilten Zufallsvariablen
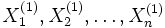 und
und 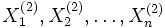 die Parameter
die Parametermit σ1 = σ2 = σ besitzen, dann unterliegt die Zufallsvariable
einer F-Verteilung mit ((n1 − 1,n2 − 1)) Freiheitsgraden. Dabei sind
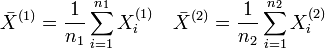 .
.
Literatur
Hartung, Joachim / Elpelt, Bärbel / Klösener, Karl-Heinz: Statistik, 12. Auflage, Oldenbourg 1999, S. 156 ff., ISBN 3486249843.
Weblinks
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.