Bruns-Eikonal

Als Eikonal (Altgriechisch εικών = Bild, Abbild) wird in der geometrischen Optik die Strecke eines Lichtstrahls zwischen Ausgangs- und Endpunkt bezeichnet; mittlerweile bezeichnet der Begriff meist das Bruns-Eikonal.

Bruns-Eikonal

Die Bruns-Eikonal oder Brunssche Eikonal ist eine Funktion welche mittels des Fermatschen Prinzips den kürzesten Weg zwischen zwei durch optische Medien getrennte Punkte beschreibt. Sie wurde vom deutschen Mathematiker Heinrich Bruns 1895 veröffentlicht.

Herleitung als Hochfrequenzapproximation der akustischen Wellengleichung

Nachfolgend soll die Eikonalgleichung als Hochfrequenzapproximation der akustischen Wellengleichung hergeleitet werden. Wir gehen also aus von der akustischen Wellengleichung mit dem Druck p, dem Ortsvektor x_i, der ortsabhängigen Ausbreitungsgeschwindigkeit c = c(x_i) und konstanter Dichte aus.

$\nabla^2 p = \frac{1}{c^2} \left(\frac{\partial}{\partial t}\right)^2 p.$

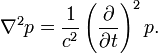
Gesucht ist ein zeitlich harmonischer Hochfrequenzansatz, für den eine frequenzunabhängige Amplitude P(x,t) und die Laufzeitfunktion φ(x) angenommen werden kann. Sie hat die Form $p(x_i,t)=P(x_i)\mathbb{e}^{i\omega(t-\phi(x_i))}.$

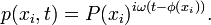
Wegen der vektoriellen Identität 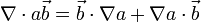$\nabla \cdot a\vec{b} = \vec{b} \cdot \nabla a + \nabla a \cdot \vec{b}$ ist auch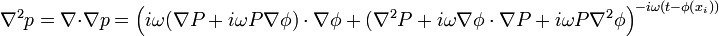 $\nabla^2p =\nabla \cdot \nabla p = \left( i\omega (\nabla P + i\omega P \nabla \phi) \cdot \nabla \phi + (\nabla^2P+i\omega\nabla\phi\cdot\nabla P + i \omega P \nabla^2\phi \right)^{-i\omega(t-\phi(x_i))}$

Die obige Gleichung kann demnach auch geschrieben werden als $-\omega P\left( (\nabla \phi)^2- \frac{1}{c^2} \right) +\omega \left( 2i \nabla P \cdot \nabla \phi + iP \nabla^2 \phi \right) + \nabla^2P = 0.$

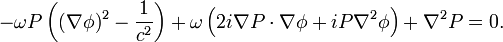
Eine Division durch − ω²P führt dann zu $\left( (\nabla \phi)^2- \frac{1}{c^2} \right) -\frac{1}{\omega P} \left( 2i \nabla P \cdot \nabla \phi + iP \nabla^2\phi \right) - \frac{1}{\omega^2 P} \left( \nabla^2P \right) = 0.$

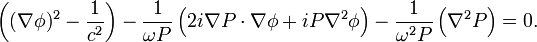
Die obige Gleichung besteht aus drei Termen mit Faktoren, die abhängig von ω sind. Für sehr hohe Frequenzen ω ist der Faktor ω ^{− 1} des zweiten Terms dann klein und der Faktor ω ^{− 2} des dritten Terms noch kleiner. Da gleichzeitig weder die Laufzeit φ noch die Amplitude P frequenzabhängig sind, sind die Produkte des zweiten und dritten Terms für sehr hohe Frequenzen sehr klein gegenüber dem ersten Term und die Gleichung vereinfacht sich auf $\left(\nabla \phi \right)^2=\frac{1}{c^2}.$

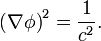
Die Lösung der Eikonalgleichung φ ordnet jedem Punkt im Ortsraum die Laufzeit der Welle zu. Linien gleicher Laufzeit lassen sich entsprechend als Wellenfronten interpretieren.

Sonstiges

Das Bruns-Eikonal wird auch in der Seismologie zur Berechnung der Ausbreitung seismischer Wellen verwendet.

Siehe auch

• Charakteristische Funktion