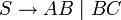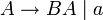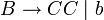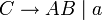- CYK
-
Der Cocke-Younger-Kasami-Algorithmus (CYK-Algorithmus) ist ein Algorithmus aus dem Gebiet der Theoretischen Informatik. Mit ihm lässt sich feststellen, ob ein Wort zu einer bestimmten kontextfreien Sprache gehört. In der Fachsprache bezeichnet man dies als Lösen des Wortproblems für kontextfreie Sprachen. Mit Hilfe von Backtracking kann der Parse-Tree bzw. die Parse-Trees eines gegebenen Wortes der Sprache konstruiert werden. Um den Algorithmus anzuwenden, muss zu der vorgegebenen Sprache eine Grammatik in Chomsky-Normalform vorliegen. Der Ende der 1960er Jahre von John Cocke, Tadao Kasami, Jacob Schwartz und Daniel Younger unabhängig voneinander entwickelte Algorithmus nutzt das Prinzip der dynamischen Programmierung.
Inhaltsverzeichnis
Beschreibung
Als Eingabe erhält der Algorithmus eine kontextfreie Grammatik G = (N,T,P,S) in Chomsky-Normalform und das zu prüfende Wort
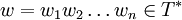 . Nun wird für jedes Teilwort
. Nun wird für jedes Teilwort 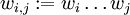 die Menge der Nichtterminale berechnet, die wi,j erzeugen, bezeichnet durch Vi,j.
die Menge der Nichtterminale berechnet, die wi,j erzeugen, bezeichnet durch Vi,j.Gemäß dem Prinzip der dynamischen Programmierung werden erst die Vi,j für die kleinsten Teilwörter von w berechnet, abgespeichert und dann zur somit effizienten Berechnung der nächstgrößeren Teilwörter weiterverwendet. Die kleinsten Teilwörter sind einzelne Buchstaben. Da die kontextfreie Grammatik in Chomsky-Normalform gegeben ist, kann jeder Buchstabe nur in genau einem Schritt von einem Nichtterminal abgeleitet werden.
Ein Nichtterminal einer Grammatik in Chomsky-Normalform kann in einem Schritt nicht auf mehrere Terminale abgeleitet werden. Daher kann ein Teilwort wi,j, das mehr als nur ein Zeichen enthält, von A nur über eine Regel
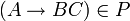 erzeugt werden. Da Nichtterminale nicht das Leere Wort (ε) erzeugen können, muss B den linken und C den rechten Teil von wi,j erzeugen. Daraus folgt:
erzeugt werden. Da Nichtterminale nicht das Leere Wort (ε) erzeugen können, muss B den linken und C den rechten Teil von wi,j erzeugen. Daraus folgt: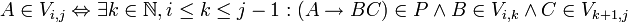
Mit anderen Worten: A kann wi,j erzeugen, wenn es gemäß der Produktionsregeln auf BC abgeleitet werden kann und B und C wiederum auf wi,k und wk + 1,j abgeleitet werden, also
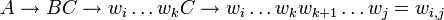 .
.Das Wortproblem kann nun einfach entschieden werden: w kann genau dann von der Grammatik erzeugt werden, wenn
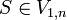 gilt. In V1,n liegen alle Variablen, die das Teilwort vom ersten bis zum letzten Buchstaben erzeugen kann, also das ganze Wort.
gilt. In V1,n liegen alle Variablen, die das Teilwort vom ersten bis zum letzten Buchstaben erzeugen kann, also das ganze Wort.Algorithmus
Aus der Beschreibung ergibt sich folgender Algorithmus:
Für i = 1 ... n Für jede Produktion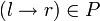 Falls r = wi
Setze
Falls r = wi
Setze 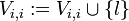 Für j = 2 ... n
Für i = j-1 ... 1
Für k = i ... j - 1
Für jede Produktion
Für j = 2 ... n
Für i = j-1 ... 1
Für k = i ... j - 1
Für jede Produktion 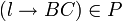 Falls
Falls 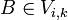 und
und 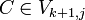 Setze
Setze 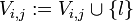 Falls
Falls 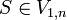 , stoppe und gib w wird von G erzeugt aus
Stoppe und gib w wird nicht von G erzeugt aus
, stoppe und gib w wird von G erzeugt aus
Stoppe und gib w wird nicht von G erzeugt aus
Beispiel
Die Fragestellung lautet, ob sich das Wort w, w = bbabaa durch die Grammatik G = ({S,A,B,C},{a,b},P,S) erzeugen lässt. Die Produktionen P der Grammatik seien:
Den Algorithmus kann man mittels einer Tabelle durchführen. Dabei ist in der i-ten Zeile und j-ten Spalte Vi,j gespeichert, also die Menge der Nichtterminalsymbole aus denen sich das Teilwort
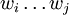 ableiten lässt.
ableiten lässt.Vi,j 1 2 3 4 5 6 1 {B} {} {A} {S,C} {B} {A,S} 2 {B} {S,A} {S,C} {B} {A,S} 3 {A,C} {S,C} {B} {S,A} 4 {B} {A,S} {} 5 {A,C} {B} 6 {A,C} Da
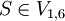 , lässt sich das gegebene Wort w = bbabaa unter der Grammatik G aus S ableiten. Also ist w ein Wort der Sprache L(G).
, lässt sich das gegebene Wort w = bbabaa unter der Grammatik G aus S ableiten. Also ist w ein Wort der Sprache L(G).Komplexität
Der Algorithmus entscheidet in der Zeit
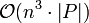 , ob ein Wort der Länge n in der in Chomsky-Normalform gegebenen Sprache L liegt.
, ob ein Wort der Länge n in der in Chomsky-Normalform gegebenen Sprache L liegt. 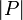 bezeichnet hier die Größe der Produktionen. Da die Grammatik in Chomsky-Normalform ist, gilt
bezeichnet hier die Größe der Produktionen. Da die Grammatik in Chomsky-Normalform ist, gilt 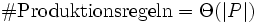 . Mit
. Mit 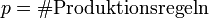 ergibt sich eine Zeitkomplexität von
ergibt sich eine Zeitkomplexität von 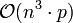 . Dabei wird Speicherplatz in der Größenordnung
. Dabei wird Speicherplatz in der Größenordnung 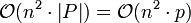 benötigt.
benötigt.Literatur
- Takao Kasami: An efficient recognition and syntax-analysis algorithm for context-free languages. In: Scientific report AFCRL-65-758. Air Force Cambridge Research Lab, Bedford 1965.
- Daniel H. Younger: Recognition and parsing of context-free languages in time n3. In: Information and Control. 10, Nr. 2, 1967, S. 189–208.
- John Cocke, Jacob T. Schwartz: Programming languages and their compilers: Preliminary notes. Courant Institute of Mathematical Sciences of New York University, New York 1970.
- Grune, Dick; Jacobs, Ceriel J. H.: Parsing Techniques: A Practical Guide. 1. Auflage. Ellis Horwood, New York 1990, ISBN 0-13-651431-6, S. 81-104 (PDF, 1.9 MB).
Weblinks
Wikimedia Foundation.