CIECAM02

CIECAM02 ist ein Farberscheinungsmodell (engl. Color Appearance Model) von der internationalen Beleuchtungskommission CIE (commission internationale de l'éclairage) und der Nachfolger von CIECAM97.

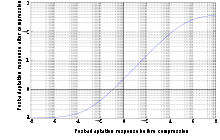
Es basiert auf dem CIECAM97-Modell und beinhaltet einige Revisionen und Vereinfachungen. Dazu gehören eine lineare chromatische Adaptionstransformation, eine Nachadaption mittels hyperbolischer Kompressionsantwortfunktion und Änderungen bei den Wahrnehmungsparametern.

Die zwei wesentlichen Bestandteile des Farberscheinungsmodells sind die chromatische Adaptionstransformation CIECAT02 und Gleichungen zur Berechnung der mathematischen Entsprechungen von Wahrnehmungsattributen wie Leuchtdichte (brightness), Helligkeit (lightness), Buntheit (chroma), Sättigung (saturation), Farbigkeit (colorfulness) und Buntton (hue). Dies sind die sechs technisch definierten Dimensionen einer Farberscheinung.

CIECAM02 berücksichtigt den Stevens Effekt, den Hunt Effekt, die Bartleson-Breneman Erscheinungen, den Simultankontrast, discounting the illuminant und die unvollständige Adaption. Im Vergleich zum vollständigen Hunt Farberscheinungsmodell wird der Übergang von Tag- zu Nachtsehen nicht berücksichtigt. Das Modell eignet sich somit nur für einen begrenzten Helligkeitsbereich und ist als nicht vollständig anzusehen, bietet im Gegenzug aber auch eine verhältnismäßig geringe mathematische Komplexität und eignet sich dementsprechend besonders für praktische Anwendungen. Zudem ist es verhältnismäßig einfach invertierbar.

Das Modell kann verwendet werden, um die Attribute der Farberscheinung vorherzusagen bzw. um entsprechende Farbwerte in einer veränderten Umgebung zu berechnen. CIECAM02 wird im Windows Color System (WCS) von Windows Vista verwendet.

Parameter für die Beobachtungsumstände

Das Beobachtungsfeld

Modell des menschlichen Beobachtungsfeldes (adaptives Feld)

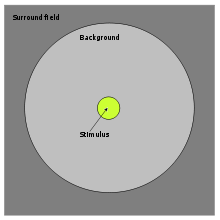
CIECAM02 verwendet ein leicht reduziertes Modell des Beobachtungsfeldes, wie es im Hunt-Farberscheinungsmodell verwendet wird. In dem Modell repräsentiert der innere Kreis den Stimulus, welcher basierend auf den Funktionen des CIE 2°-Standardbeobachters die Tristimulus-Werte (XYZ)^T liefert. Der äußere Kreis ist der 10° umfassende Hintergrund, in welchem die relative Helligkeit des Hintergrundes Y_b gemessen wird. Außerhalb des runden Blickfeldes liegt die Umgebung (peripheres Gebiet), welche den restlichen Raum darstellt. Die Gesamtheit von Hintergrund und Umgebung nennt sich das adaptive Feld.

Für praktische Anwendungen kann dieses Modell jedoch nicht als Maßgeblich sondern nur als Grundlage angesehen werden und muß den Umständen entsprechend angepasst werden. In der Bildverarbeitung z.B. ist der Stimulus meist von einem einzelnen Pixel definiert und die Helligkeit des Hintergrundes wird mit der eines neutralen grautons(20%) definiert, da der Hintergrund durch die von der Umgebungssituation unabhängigen räumlichen Helligkeitsverteilung innerhalb eines Bildes nicht großartig variiert. Der Hintergrund wäre zudem mit der festen Definition seiner Ausmaße von 10° abhängig von der Skalierung des Bildes und dem Betrachtungsabstand möglicherweise mehrerer Beobachter. Dasselbe gilt für einen Stimulus mit 2° Ausmaßen.

Weißpunkt und absolute Helligkeit

Zwei weitere Elementare Parameter für CIECAM02 sind der Weißpunkt (X_wY_wZ_w)^T und die absolute Helligkeit des adaptiven Feldes L_A. Der Tristimuluswert des Weißpunkts basiert ebenfalls auf dem CIE 2°-Standardbeobachter und wird generell von der vorhandenen Lichtquelle definiert. Im Falle von selbstleuchtenden Medien wie Monitoren oder Projektionen liegt dieser jedoch zwischen dem Weißpunkt der Lichtquelle und dem des Mediums selbst, wobei hier wiederum keinerlei feste Definitionen vorliegen. Mit ermittelten Weißpunkt wird der XYZ-Raum in welchem sich sowohl der Weißpunkt als auch der Stimulus befinden auf Y_w = 100 normalisiert.

Die absolute Helligkeit des adaptiven Feldes L_A kann zum einen mit einem Photometer gemessen werden. Falls keines vorhanden ist kann für den generellen Fall angenommen werden, daß das adaptive Feld eine graue(20%) Fläche ist (grey-world-assumption), und L_A nimmt dementsprechend den Wert von 20% der vorhandenen Umgebungshelligkeit an. Hat das betrachtete Medium eine höhere absolute Helligkeit als die Umgebung, wie z.B. bei einer Projektion in einem dunklen Raum so wird die Helligkeit des Mediums als maßgeblich erachtet.

Umgebungsparameter

Die Umgebungsparameter lassen sich über das Verhätnis der absoluten Helligkeit der Umgebung und jener des Stimulus bestimmen und sind in der folgenden Tabelle festgehalten:

Umgebungsfeld	F	c	Nc
durchschnittlich	1.0	0.69	1.0
dämmerig	0.9	0.59	0.95
dunkel	0.8	0.525	0.8

F: Adaptionsgrad

c: Umgebungsauswirkung

N_c : Faktor für chromatische Induktion

In den meisten Fällen liegen durchschnittliche Umgebungsparameter vor. Eine dämmerige Umgebeng ist gegeben, wenn die absolute Helligkeit der Umgebung bei 20% der Helligkeit eines selbstleuchtenden Mediums liegt. Von einer dunklen Umgebung spricht man, wenn nahezu kein Umngebungslicht vorhanden ist, z.B. bei einer Projektion in einem dunklen Raum. Für nicht selbstleuchtende Medien geht man generell von „durchschnittlichen“ Umgebungsparametern aus.

Für Zwischenstufen können diese Werte linear interpoliert werden.

Praktische Anwendung

Die Spezifikationen der Eingangsparameter sind, wie schon angedeutet, recht vage gehalten und erfordern eine den Umständen entsprechende Interpretation.

Folgende Tabelle enthält einige Vorschläge für vier mögliche Anwendungsfälle, wobei im vierten Fall die Bestimmung von L_A in Anbetracht der Erhöhten Umgebungshelligkeit fraglich bleibt:

Beispielparameter für CIECAM02

Umgebungssituation	Umgebungslicht in lux (cd / m2)	Helligkeit des Szenenweißpunktes in cd / m2	LA in cd / m2	Weißpunkt	Umgebungsparameter
Farbige Oberfläche in einer Lichtkammer	1000 (318.3)	318.3	63.66	WP der Lichtkammer	durchschnittlich
Fernsehabend	38(12)	80	16	Zwischen WP der Umgebung und des Fernsehers	dämmerig
Projektion in abgedunkelten Raum	0(0)	150	30	Zwischen WP des Projektors und E(equal energy ill.)	dunkel
Computermonitor im Büro	500(159.2)	80	16	Zwichen WP des Monitors und der Bürobeleuchtung	durchschnittlich

Ein weiterer Punkt ist die Bestimmung der Tristimulus-Werte. Liegt der Stimulus in Form eines selbstleuchtenden Mediums vor, können die Werte mithilfe der Photometrischen Daten des Mediums bestimmt werden. Im Falle von nicht selbstleuchtenden Medien ist der Stimulus durch das Spektrum Lichtquelle und die filternden Eigenschaften des mediums bestimmt, was die Bestimmung der Parameter deutlich erschwert. Bezüglich des Weißpunktes muß man ähnlich vorgehen.

Chromatische Adaptionstransformation

Zäpchenantworten für CAT02 und HPE

Die chromatische Adaptionstransformation von CIECAM02 zeichnet sich vor allem dadurch aus, daß sie in zwei verschiedenen Farbräumen stattfindet. Zuerst wird eine modifizierte von Kries Adaptionstransformation in einem modifizierten Li et al. RGB-Raum durchgeführt, der durch eine erhöhte spektrale Schärfe der R und B Komponenten im Vergleich zu den natürlichen spektralen Antworten der Zapfen gekennzeichnet ist. Die chromatische Adaptionstransformation ist eine modifizierte CMCCAT2000 und wird als CIECAT02 bezeichnet. Bei der Entwicklung von CIECAM02 lag das Hauptaugenmerk auf einer Linearisierung der Bradford-Transformation aus CIECAM97s, welche eine exponentielle nichtlinearität im Blaukanal hatte und so eine analytische invertierung verunmöglichete. Die Ergebnisse der CIECAT02 wurden mit psychophysischen Messdaten verglichen und erwiesen sich Abwärtskompatibel, wenn nicht sogar besser, verrglichen mit der Transformation aus CIECAM97s. Die adaptierten Farbwerte werden anschließend über den XYZ-Farbraum in den Hunt-Pointer-Estevez-Raum übertragen und einer Nachadaption in Form einer Komressionsantwortfunktion unterzogen. Der HPE-Raum eignet sich für die weiteren Schritte, da seine spektralen Antwortfunktionen eher den natürlich in den Zapfen vorkommenden gleicht. Aus dem Hunt-Pointer-Estevez Raum heraus werden später auch die Wahrnehmungsparameter bestimmt bzw. die ermittelten Farbwerte in den 5-dimensionalen JChQM Farbraum übertragen.

CIECAT02

Grad der Adaption D(L_A,F)

Grad der Adaption

Um die Tristimuluswerte in den Li et al. RGB-Farbraum zu übertragen, wird folgende Matrix verwendet:

$M_{CAT02} = \begin{bmatrix} 0.7328 & 0.4296 & -0.1624\\ -0.7036 & 1.6975 & 0.0061\\ 0.0030 & 0.0136 & 0.9834 \end{bmatrix}$

Die inverse Matrix, welche für die Rücktransformation in den XYZ-Farbraum benötigt wird, hat folgende Form:

$M^{-1}_{CAT02} = \begin{bmatrix} 1.0961 & -0.278869 & 0.182745\\ -0 454369 & 0.473533 & 0.072098\\ 0.009628 & 0.005698 & 1.015326 \end{bmatrix}$

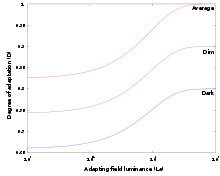
Für die chromatische Adaption wird noch der von L_A und F abhängige Grad der Adaption D benötigt: $D=F \left( 1-\frac{1}{3.6} e^\frac{-L_A-42}{92} \right)$

Falls der Stimulus einem nicht selbstleuchtenden Medium entspringt wird D = 1 angenommen, da hier von einer vollständigen Adaption des visuellen Systems an das Leuchtmittel auszugehen ist (discounting the illuminant). Die vollständige CIECAT02 Transformation lässt sich dann wie folgt ausdrücken:

$\begin{bmatrix} X'\\Y'\\Z' \end{bmatrix} = M^{-1}_{CAT02} \begin{bmatrix} \frac{Y_w D}{R_w}+(1-D) & 0 & 0 \\ 0 & \frac{Y_w D}{G_w}+(1-D) & 0 \\ 0 & 0 & \frac{Y_w D}{B_w}+(1-D) \end{bmatrix} M_{CAT02} \begin{bmatrix} X\\Y\\Z \end{bmatrix}$

Für RGB-Werte des Weißpunktes müssen auch dessen Tristimulus-Werte in den CAT02-Raum übertragen werden. Ausgehend von der Normalisierung der Tristimuluswerte auf Y_w = 100 ändert sich CIECAT02 zu:

$\begin{bmatrix} X'\\Y'\\Z' \end{bmatrix} = M^{-1}_{CAT02} \begin{bmatrix} \frac{100 D}{R_w}+(1-D) & 0 & 0 \\ 0 & \frac{100 D}{G_w}+(1-D) & 0 \\ 0 & 0 & \frac{100 D}{B_w}+(1-D) \end{bmatrix} M_{CAT02} \begin{bmatrix} X\\Y\\Z \end{bmatrix}$

Nachadaption

luminance level adaption factor F_L(L_A)

Kompressionsantwortfunktion R'_A(L_A,R')

Kompressionsantwortfunktion (F_L = 1)

Die Nachadaption sorgt für eine Berücksichtigung des Hunt- und des Stevens-Effekts. Zum einen wird die Transformationsmatrix in den HPE-Farbraum benögt:

$M_{HPE} = \begin{bmatrix} 0.38971 & 0.68898 & -0.07868\\ -0.22981 & 1.18340 & 0.04641\\ 0.00000 & 0.00000 & 1.00000 \end{bmatrix}$

Mit ihr werden die voradaptierten Tristimulus-Werte in den HPE-Raum abgebildet:

$\begin{bmatrix} R'\\G'\\B' \end{bmatrix} = M_{HPE} \begin{bmatrix} R'\\G'\\B' \end{bmatrix}$

Um die Kompressionsantwortfunktion zu berechnen, wird noch der „luminance-level adaption factor“ F_L benötigt, der direkt aus L_A berechnet werden kann.

F_L = 0.2k⁴(5L_A) + 0.1(1 − k⁴)²(5L_A)^{1 / 3}

mit

$k = \left(\frac{1}{5L_A+1}\right)$

Die Kompressionsantwortfunktion für den Rotwert gestaltet sich wie folgt:

$R'_a=\left( \frac{400\left(\frac{F_LR'}{100}\right)^{0.42}}{\left[27.13+\left(\frac{F_LR'}{100}\right)^{0.42}\right] } \right)+0.1$

Der Zusammenhang kann in der selben Form auf die Grün- und Blauwerte angewendet werden. Es gilt zu beachten, daß hier mit den Beträgen von R', G' und R' gearbeitet und ein eventuelles negatives Vorzeichen auf das Ergebnis übertragen werden muß.

Wahrnehmungsparameter

Die Wahrnehmungsparameter werden direkt aus den komprmierten RGB-Werten im HPE-Raum berechnet und spannen einen 5-dimensionalen Wahrnehmungsfarbraum auf. Die Wahrnehmungsparameter sind der Farbton oder Buntton (hue) h, relative Helligkeit (lightness) J, die absolute Helligkeit (brightness) Q, Farbigkeit oder relative Buntheit (chroma) C, absolute Buntheit (colorfulness) M und die Sättigung (Saturation) s, welche an sich ein redundanter Parameter ist und dementsprechend keine eigenständige Dimension aufspannt.

Vorberechnungen

Während für die chromatische Adaption nur die absolute Helligkeit des Adaptiven Feldes und die Umgebungsparameter von Bedeutung waren, kommt der relativen Helligkeit des Hintergrundes Y_b nun bei der Berechnung der psychophysischen Größen eine wesentliche Bedeutung zu, da dieser ja durch eventuell vorhandene Simultankontraste Einfluß auf die subjektive Farbwahrnehmung hat. Aus Y_b lassen sich folgende Parameter bestimmen:

$n=\frac{Y_b}{Y_w}$

$N_{bb} = N_{cb} = 0.725\left(\frac{1}{n}\right)^{0.2}$

$z = 1.48 + \sqrt{n}$

N_bb und N_cb stehen dabei für den achromatischen und den chromatischen Induktionsfaktor des Hintergrundes und sind somit ein Maß dafür, inwieweit sich dieser auf die Wahrnehmung des Stimulus auswirkt und genügen somit dem Simultankontrast. Unter der weiter oben eingeführten Annahme, daß der Hintergrund ein grau(20%) ist, werden N_bb und N_cb zu 1. z drückt den selben Zusammenhang aus, wird jedoch im folgenden als Exponent und nicht als Faktor auftauchen. Aus den Farbwerten im HPE-Raum lassen sich zunächst vorläufige kartesische Koordinaten in einer rot-grün(a) und gelb-blau(b) Metrik berechnen.

$a=R'a-\frac{12G'_a}{11}+\frac{B'_a}{11}$

$b=\left( \frac{1}{9} \right)(R'_a+G'_a-2B'_a)$

Buntton (Hue) H

Der Buntton H in anderen ist wie auch in anderen Farbräumen über den Winkel von (a,b)^T definiert.

$h=tan^{-1}\left (\frac{b}{a}\right)$

In Abhängigkeit von diesem lässt sich der Exzentrizitätsfaktor berechnen, welcher später auf die Berechnung von Buntheit bzw. Farbigkeit einen Einfluß hat, indem er die von (a,b)^T aufgespannte Ebene in Abhängigkeit vom Winkel dehnt oder staucht. So wird der Tatsache genüge getan, daß die Höhe der Buntheit bzw. Farbigkeit in Abhängigkeit vom Farbton definiert wird.

$e=\frac{1}{4}\left[ cos\left(h\frac{\pi}{180}+2\right)+3.8\right]$

Die Bunttonquadratur H, ein an sich vollkommen redundanter Wert, der jedoch den vier die Metrik definierenden Farben ein vielfaches von 100 zuordnet und somit eine Daseinsberechtigung hat, wird durch lineare Interpolation über die Werte folgender Tabelle gewonnen.

	Rot	Gelb	Grün	Blau	Rot
i	1	2	3	4	5
hi	20.14	90.00	164.25	237.53	380.14
ei	0.8	0.7	1	1.2	0.8
Hi	0	100	200	300	400

$H=H_i+\frac{100\frac{(h-h_i)}{e_i}}{\frac{(h-h_i)}{e_i}+\frac{(h_{i+1}-h)}{e_{i+1}}}$

Relative Helligkeit (Lightness) J

Um die relative Helligkeit zu berechnen wird vorab eine Achromatische Antwort mittels einer gewichteten Summation der Farbwerte berechnet, welche zusätzlich noch einen den Schwarzpunkt defineirenden Rauschterm beinhaltet. Die Summe wird zudem noch mit dem achromatischen Induktionsfaktor des Hintergrundes gewichtet.

$A=\left[2R'_a+G'_a+\left( \frac{1}{20} \right)B'_a-0.305\right]N_{bb}$

Die relative Helligkeit an sich ergibt sich dann aus dem Verhältnis der Achromatischen Antwort des Stimulus und der des Weißpunkts. Der Weißpunkt muß bis zu diesem Punkt den selben Transformationen unterzogen werden wie der Stimulus selbst um seine Achromatische Antwort zu erhalten. Der vom Hintergrund und der Umgebung vorgegebene Exponent sorgt für eine kovexe bzw konkave Krümmung des funktionalen Zusammenhangs und sorgt somit für eine Berücksichtigung des Simultankontrasts über z und der Bartleson-Breneman Gleichungen über c. $J=100\left( \frac{A}{A_w} \right)^{cz}$

Absolute Helligkeit (Brightness) Q

Die Bestimmung der absoluten aus der relativen Helligkeit des Stimulus ist im Grunde genommen eine Umkehrung der bisher vorgenommenen psychophysischen Anpassungen. Die absoulute Helligkeit des adaptiven Feldes wirkt sich zwar nicht auf die wahrgenommene relative Helligkeit des Stimulus aus, aber die absolute Helligkeit wird durchaus von ihr beeinflusst. Dementsprechend taucht hier der auch schon in der Kompressionsantwortfunktion zu Rate gezogene „luminance level adaption factor“ F_L wieder auf. Auch A_w und c werden hier in einem zu den bisherigen Anwendungen reziproken Sinne verwendet.

$Q=\left( \frac{4}{c} \right)\sqrt{\left( \frac{J}{100} \right)}(A_w+4)F_L^{0.25}$

Buntheit (Chroma) C

Die Berechnung der Buntheit erfordert die Berechnung einer vorläufigen Größe t, welche eine Betragsbildung von (a,b)^T enthält. Hier enthalten sind zudem der Exzentritätsfaktor e sowie die chromatischen Induktionen der Umgebung und des Hintergrundes N_c und N_cb.

$t=\frac{(50000/13)N_cN_{cb}e(a^2+b^2)^{1/2}}{R'_a+G'_a+\left( \frac{21}{20} \right)B'_a}$

Über t wird dann die Buntheit C unter Hinzunahme von n berechnet. Die helligkeit des Hintergrundes wirkt sich so auch auf die wahrgenommene Farbintensität aus.

$C=t^{0.9}\sqrt{\frac{J}{100}}(1.64-0.29^n)^{0.73}$

Farbigkeit (Colorfulness) M

Genau, wie auch bei der Berechnung der absoluten Helligkeit, wirkt sich im Gegensatz zu der relativen Buntheit eine Erhöhung der Helligkeit des adaptiven Feldes auf die Farbigkeit bzw. die absolute Buntheit aus. So taucht auch hier wieder der „luminance level adpation factor auf“.

$M=CF_L^{0.25}$

Sättigung (Saturation) S

Die Sättigung ist wie zuvor schon erwähnt eine im Sinne des CIECAM02 redundante Größe und lässt sich direkt aus Farbigkeit M und absoluter Helligkeit Q berrechnen.

$s=100\sqrt{ \frac{M}{Q}}$

Kartesische Koordinaten

In einigen Fällen kann eine Darstellung einzelner Stimuli in kartesischen Koordinaten von Vorteil sein. Für den relativen psychophysisch relevanten JCh-Raum seien hier die trigonometrischen Zusammenhänge aufgeführt. Zusammen mit J spannen a_c und b_c den dreidimensionalen Raum auf. a_c und b_c dürfen nicht mit den vorläufigen Kartesischen Koordinaten a und b verwechselt werden. Der hier vorliegende Raum erfährt relativ zum ursprünglich aufgespannten durch e eine exzentrische Krümmung sowie diverse von Y_b und L_a verursachte Skalierungen über der Farbebene.

a_c = Ccos(h)

b_c = Csin(h)

Für den QMh-Raum oder QMs-Raum können entsprechende Zusammenhänge hergestellt werden.

Quellen

• http://www.polybytes.com/misc/Meet_CIECAM02.pdf
• http://www.cis.rit.edu/fairchild/PDFs/AppearanceLec.pdf
• http://www.uni-koblenz.de/~cg/ss09/Proseminar_Farbmanagement/CIECAM02.pdf