Cardanische Kreise

Als Cardanische Kreise werden die zwei Kreise bezeichnet, mit denen durch Abrollen eines Kreises im Inneren eines Kreises mit doppeltem Radius durch jeden Punkt des rollenden Kreises eine geradlinige Hypozykloide erzeugt wird. Dieser Zusammenhang wurde 1570 erstmals von dem italienischen Humanisten Gerolamo Cardano beschrieben. Es handelt sich hier um frühe Untersuchungen zu Zykloiden, die später von Galilei ausgeweitet wurden.

Abbildung zu den „Kreisen von Cardano“

Formulierung des Satzes von Cardano

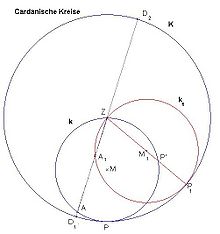
Gegeben ist ein Kreis k mit Mittelpunkt M und Radius r, der in einem Kreis K mit Mittelpunkt Z und dem doppelten Radius R=2r liegt und diesen im Punkt P berührt. Der Kreis k werde durch Rollen auf dem Rand des Kreises K auf den Kreis k₁ abgebildet und P₁ bezeichne den Berührpunkt von k₁ mit K.

Dann gilt:

(i) Ist P' der Schnittpunkt von $\overline{Z P_1}$ mit dem Kreis k dann sind die Kreisbögen PP' und PP₁ gleichlang.

(ii) Ist A ein beliebiger Punkt auf dem Kreis k, dann liegt sein Bildpunkt A₁ auf dem Durchmesser $\overline{D_1 D_2}$ von K, der durch die Gerade durch A und Z bestimmt ist.

(iii) Wird k bis in seine Ausgangangslage gerollt, dann bewegt sich der Punkt A geradlinig auf dem Durchmesser $\overline{D_1 D_2}$ und durchläuft jeden Punkt des Durchmessers genau zweimal.

In Kurzform: Rollt ein Kreis innen auf einem Kreis mit dem doppeltem Radius ab, dann bewegt sich jeder Punkt des kleinen Kreises geradlinig auf einem Durchmesser des großen Kreises.

Zusatz: Jeder Punkt im Inneren der abrollenden Kreisscheibe beschreibt bei einem Umlauf eine Ellipse, deren Mittelpunkt mit dem Mittelpunkt des großen Kreises übereinstimmt. Dies wurde 1706 von Philippe de La Hire veröffentlicht.

Technische Anwendungen

Wird der äußere Kreis innen verzahnt und der innere Kreis als Zahnrad ausgeführt, dann lässt sich über eine Stange, die im Punkt A befestigt ist und sich parallel zum Durchmesser $\overline{D_1 D_2}$ bewegt, eine Auf- und Abbewegung für Maschinen nutzen. Dieses Prinzip lag der Erfindung der Buchdruckschnellpressen von König & Bauer zugrunde.

Literatur

• Cardano, Girolamo; Opus novum de proportionibus, Basel 1570 (Archimedes Project)
• Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 2 Stuttgart, Leipzig 1905., S. 423-424.

Weblinks

• https://www.tu-chemnitz.de/mb/MechAntrTech/getriebebibliothek/DB_index.php?TAB=Getriebemodell&NR=147 (Modell zur Verwendung der Cardanischen Kreise in der Getriebetechnik)